Complete Solutions to दीर्घ उत्तरीय प्रश्न of chapter गणित 2015 of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | गणित 2015 |
| UP BOARD PREVIOUS YEAR | दीर्घ उत्तरीय प्रश्न |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
द्विघात समीकरण : `(x^2 + 12x)^2 +35(x^2 + 12x)+150 = 0` को हल कीजिए।
View Solutionद्विघात समीकरण : `(x^2-x)^2 + 5(x^2-x)+4=0` को हल कीजिए।
View Solutionरूपाली एक नाव को शांत जल में 15 किमी/घण्टे की दर से चला सकती है। धारा की दिशा में 30 किमी जाने में तथा धारा के विपरीत 30 किमी वापस आने में वह कुल 4 घण्टे 30 मिनट का समय लेती है। धारा की चाल ज्ञात कीजिए।
View Solutionएक नाव की शान्त जल में चाल 15 किमी/घण्टा है। नाव की धारा की दिशा में 30 किमी जाने और फिर धारा की विपरीत दिशा में लौटने में कुल समय 4 घण्टे 30 मिनट लगते हैं। धारा की चाल ज्ञात कीजिए।
View Solutionएक यात्री 300 किमी की दूरी तय करने में 3 घण्टे कम समय लेता है जब उसकी चाल में 5 किमी/घण्टा की वृद्धि कर दी जाती है। तब यात्री की चाल ज्ञात कीजिए।
View Solutionनिम्नलिखित बारम्बारता बंटन से माध्यिका ज्ञात कीजिए-

View Solutionनिम्नलिखित बारम्बारता सारणी से माध्यिका ज्ञात कीजिए-

View Solutionनिम्नलिखित बारम्बारता बंटन का समान्तर से माध्य 50 है | बारम्बारता `f_1` और `f_2` का मान ज्ञात कीजिए

बारम्बारताओ का कुल योग `120` है |
View Solution12 मीटर चौड़ी सड़क के एक ओर एक मीनार तथा दूसरी ओर एक मकान स्थित है। मकान के आधार से मीनार के शिखर का उन्नयन कोण `60^@` तथा मीनार के शिखर से मकान के शिखर का अवनमन कोण `45^@` है। मीनार तथा मकान की ऊँचाई ज्ञात कीजिए।
View Solutionएक हवाई जहाज, जो कि 1000 मीटर की ऊँचाई पर उड़ रहा है, पर स्थित मनुष्य उत्तर की ओर एक शत्रु की पनडुब्बी को `30^@` के अवनमन कोण पर तथा दक्षिण की ओर एक युद्धपोत को `45^@` के अवनमन कोण पर देखता है। पनडुब्बी और युद्धपोत के बीच की दूरी ज्ञात कीजिए।
View Solutionक्षैतिज तल पर स्थित बिन्दु O से उसी तल पर खड़ी एक ऊर्ध्वाधर मीनार के शीर्ष का उन्नयन कोण `15^@` है। मीनार की ओर 80 मीटर चलने पर उन्नयन कोण 30° हो जाता हैं। मीनार की ऊँचाई ज्ञात कीजिए।
View Solutionएक मीनार AB के आधार से a मीटर और 6 मीटर की दूरी पर, मीनार के आधार से जाने वाली एक ही रेखा में स्थित बिन्दुओं क्रमश: C और D से मीनार के ऊपरी सिरे के उन्नयन कोण कोटिपूरक है। सिद्ध कीजिए कि मीनार की ऊँचाई `sqrt(ab)` मीटर है।
View Solutionएक मीनार के आधार से 100 मीटर और 25 मीटर दूर उसी समतल पर स्थित दो बिन्दुओं A और B जो एक सीधी रेखा में हैं, उन पर से मीनार के उन्नयन कोण एक-दूसरे के कोटिपूरक हैं। मीनार की ऊँचाई ज्ञात कीजिए।
View Solution`DeltaABC` के अन्तर्गत एक वृत्त खींचा गया है तथा P,Q,R स्पर्श बिन्दु हैं। यदि PA = 4 सेमी, PB = 6 सेमी तथा AC = 12 सेमी हो तो BC की माप ज्ञात कीजिए।
View Solutionकिसी धातु का एक ठोस एक अर्द्धगोले के समतल पृष्ठ पर रखे एक शंकु के आकार का है। अर्द्धगोले के समतल पृष्ठ का व्यास तथा शंकु के आधार का व्यास प्रत्येक 20 सेमी है। शंकु का शीर्षकोण `90^@` है। ठोस का आयतन तथा पृष्ठ `pi` के पदों में ज्ञात कीजिए।
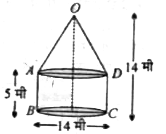
View Solutionएक तम्बू का निचला भाग लम्बवृत्तीय बेलनाकार तथा ऊपरी भाग शंक्वाकार है। यदि तम्बू के आधार का व्यास 14 मीटर है, बेलनाकार भाग की ऊंचाई 5 मीटर है और तम्बू की सम्पूर्ण मी ऊँचाई 14 मीटर है तो तम्बू का आयतन ज्ञात कीजिए।
View Solution2 सेमी त्रिज्या के एक बेलनाकार टब में 20 सेमी ऊँचाई तक पानी भरा है। लोहे की एक गोलीय गेंद टब में डाली जाती है और इस प्रकार पानी का स्तर 6.75 सेमी ऊपर उठ जाता है। गेंद की त्रिज्या ज्ञात कीजिए।
View Solutionएक ठोस लम्बवृत्तीय बेलन के दोनों सिरों में दो समान शंक्वाकार छेद बनाये गये हैं। बेलन की ऊँचाई 10 सेमी और आधार का व्यास 8 सेमी है। यदि छेद का व्यास 6 सेमी और गहराई 4 सेमी है तो शेष बचे ठोस का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
View Solutionएक लम्बवृत्तीय बेलन के आधार का क्षेत्रफल `154 "सेमी"^2` है और इसकी ऊंचाई 15 सेमी. है। इसका वक्रपृष्ठ ज्ञात कीजिए।
View Solutionएक लम्बवृत्तीय शंकु की तिर्यक ऊँचाई 13 सेमी० तथा सम्पूर्ण पृष्ठ 9pi वर्ग सेमी हैं। इसके आधार की त्रिज्या ज्ञात कीजिए।
View Solutionपीतल की एक बेलनाकार खोखली नली 21 सेमी० लम्बी है। इसके बाह्य और अन्त: व्यास क्रमश: 10 सेमी० और 6 सेमी० हैं। नली को बनाने में लगे हुए पीतल का आयतन ज्ञात कीजिए।
View Solutionनिम्नलिखित बारम्बारता सारणी से माध्यिका ज्ञात कीजिए-

View Solutionनिम्नलिखित बारम्बारता बंटन से समान्तर माध्य ज्ञात कीजिए।

View Solutionसमीकरण `1/x-1/((x+1))=1/((x+2))-1/((x+4))` को सरल करके द्विघात समीकरण प्राप्त कीजिए। मूलों की प्रकृति बताइए। सूत्र का प्रयोग करके समीकरण हल कीजिए।
View Solutionदो अंकों की संख्या के अंकों का गुणनफल 18 है। जब संख्या में से 27 घटाया जाता है तो संख्या के अंकों के स्थान बदल जाते हैं। वह संख्या ज्ञात कीजिए।
View Solutionदो अंकों की एक संख्या के अंकों का गुणनफल 14 है। संख्या में 45 जोड़ने पर अंकों के स्थान परस्पर बदल जाते हैं। संख्या ज्ञात कीजिए।
View Solutionयदि समीकरण `x^2 - px+q=0 ` के मूल `alpha` और `beta` हों तो `alpha^3 +beta^3` का मान ज्ञात कीजिए।
View Solutionसमीकरण को हल कीजिए : `sqrt(2x+9)- sqrt(x-4)-3=0`
View Solutionएक नाव की शान्त जल में चाल 15 किमी/घं है। नाव को धारा की दिशा में 30 किमी० जाने तथा धारा की विपरीत दिशा में 30 किमी० लौटने में कुल 4 घंटे 30 मिनट लगते हैं। धारा की चाल ज्ञात कीजिए।
View Solutionसमीकरण हल कीजिए :
`((x-1)/(x+1))^4 -13 ((x-1)/(x+1))^2 + 36 =0`
View Solutionदो अंकों की एक संख्या में अंकों का जोड़ 12 है। अंकों के स्थान बदलने पर प्राप्त संख्या दी गई संख्या से 18 अधिक है। संख्या ज्ञात कीजिए।
View Solutionएक पैराशूट धारक (Parachutist) ऊ र्ध्वाधर उतर रहा है । वह अपने से बाईं ओर एक दूसरे से 100 मी. दूर स्थित दो प्रेक्षण बिंदुओं पर `45^(@)` और `60^(@)` का अवनमन कोण बनाता है। जहाँ से वह गिरता है, वह ऊँचाई मी. (लगभग) में ज्ञात कीजिए । प्रथम प्रेक्षण बिंदु से उसके भूमि पर उतरने वाले बिंदु की दूरी मी. (लगभग) में ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए :
`((cottheta)/("cosec" theta+1))+(("cosec" theta+1)/(cottheta))=2 sec theta`
View Solutionसिद्ध कीजिए :
` 5^{89} - 401` अभाज्य संख्या नहीं है
View Solutionभूमि पर स्थित एक चिह्नित बिन्दु से एक मीनार की चोटी का उन्नयन कोण `45^@` है। मीनार के पाद की ओर भूमि पर 40 मीटर चलने पर मीनार की चोटी का उन्नयन कोण `60^@` हो जाता है। चिह्नित बिन्दु की मीनार के पाद से दूरी ज्ञात कीजिए।
View Solutionसिद्ध कीजिए : `tan^(2) theta + cot^(2) theta + 2 = sec^2 . "cosec"^2 theta`
View Solutionहल कीजिए : `("cos theta)/(1-sin theta)+(cos theta)/(1+sin theta) =4`
View Solution3 सेमी त्रिज्या का एक वृत्त खींचिए। वृत्त के केन्द्र से 7 सेमी दूर एक बाह्य बिन्दु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए। रचना के पद भी लिखिए।
View Solution4 सेमी त्रिज्या का एक वृत्त खींचिए। वृत पर दो स्पर्श रेखाओं की रचना कीजिए जिनके बीच के कोण की माप `60^@` हो। रचना पद भी लिखिए।
View Solution5 सेमी त्रिज्या का एक वृत्त खींचिए। वृत के केन्द्र से 13 सेमी दूर एक बाह्य बिन्दु से वृत पर स्पर्श रेखा युग्म की रचना कीजिए। रचना पद भी लिखिए।
View Solution2.5 सेमी त्रिज्या का एक वृत्त खींचिए। वृत्त के केन्द्र से 6.5 सेमी० दूर स्थित एक बिन्दु से वृत्त पर दो स्पर्श रेखाएँ खींचिए। स्पर्श रेखाओं की माप ज्ञात कीजिए।
View Solution
दीर्घ उत्तरीय प्रश्न questions and complete solutions for chapter गणित 2015 of UP BOARD PREVIOUS YEAR of Class 10