Complete Solutions to लघु उत्तरीय प्रश्न्नोत्तर of chapter पृष्ठीय क्षेत्रफल और आयतन of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | पृष्ठीय क्षेत्रफल और आयतन |
| UP BOARD PREVIOUS YEAR | लघु उत्तरीय प्रश्न्नोत्तर |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
12 सेमी वाले त्रिजयखंड का कोण `120^(@)` है| इस त्रिजयखंड को इस प्रकार मोड़ा गया है उसके दो किनारे त्रिज्याओं को एक साथ जोड़कर शंकु प्राप्त होता है| शांतु का आयतन ज्ञात कीजिए|
View Solutionएक लंबवर्तीय शंकु की त्रिज्या और ऊंचाई 3:4 के अनुपात में है| यदि इसका आयतन 301.44 `cm^(3)` हो, तो शंकु की त्रिज्या ज्ञात कीजिए| `(pi = 3.14)`
View Solution24 सेमी व्यास और 6 सेमी ऊँचे एक लम्ब वृतीय शंकु को पिघलाकर बनाए गए ठोस गोले का पृष्ट क्षेत्रफल ज्ञात कीजिए|
View Solutionलोहे की एक ठोस गेंद की त्रिज्या 9 सेमी है। इसे पिघलाकर तीन छोटी गेंदे बनायी गयी है| यदि उनमे से दो त्रिज्याएँ क्रमश: 8 सेमी और 6 सेमी है, तो तीसरी गेंद की त्रिज्या ज्ञात कीजिए।
View Solutionएक गोला जिसका व्यास `12` सेमी है, एक लंब वृत्तीय बेलनाकार बर्तन में डाला जाता है जिसमे पानी भरा है। यदि गोला पानी में पूरा डूब जाता है तो बेलनाकार बर्तन में पानी की सतह `3 5/9` सेमी बढ़ जाती है, तो बेलनाकार बर्तन का व्यास ज्ञात कीजिए।
View Solution6.0 सेमी त्रिज्या और 2.0 डेमी ऊंचाई के एक ठोस बेलन को पिघलाया जाता है और उससे एक लांब वृत्य शंखू, जिसकी ऊंचाई बेलन की ऊंचाई की तीन गुनी है, बनाया जाता है| शंकु का वक्र पृष्ट ज्ञात कीजिए|
View Solutionमीटर व्यास का एक कुँआ 14 मीटर की गहराई तक खोदा जाता है| इससे निकली हुई मिट्टी को कुएं के चारों ओर 4 मीटर चौड़ी एक वृत्ताकार वलय (Ring) बनाते हुए, समान रूप से फैलाकर एक प्रकाश का बाँध बनाया जाता है| इस बाँध की ऊंचाई ज्ञात कीजिए|
View Solutionत्रिज्या 4.2 सेमी वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 सेमी वाले एक बेलन के रूप में डाला जाता है| बेलन की ऊंचाई ज्ञात कीजिए|
View Solutionएक धातु के ठोस गोले का व्यास 6 सेमी है| गोले को पिघलाकर एकसमान आकार का तार बनाया गया है| यदि तार की लम्बाई 36 सेमी है, तो तार का व्यास ज्ञात कीजिए|
View Solutionएक शंकवाकार बर्तन जिसके आधार की त्रिज्या 5 सेमी ओर ऊंचाई 24 सेमी है, पानी से पूरा भरा है| इस पानी को एक बेलनाकार बर्तन में पलटा जाता है, जिसके आधार की त्रिज्या 10 सेमी है| बेलनाकार बर्तन में पानी की ऊंचाई ज्ञात कीजिए `(pi = 22/7)`
View Solutionशंक्वाकार बर्तन, जिसका आंतरिक व्यास 10 सेमी है ओर ऊंचाई 24 सेमी है, पानी से भरा है| पानी को एक बेलनाकार पात्र, जिसका आंतरिक व्यास 20 सेमी है में डाला जाता है| बेलनाकार पात्र में डाले गए पानी की ऊंचाई ज्ञात कीजिए|
View Solution32 सेमी ऊँची ओर आधार त्रिज्या 18 सेमी वाली एक बेलनाकार वाल्ती रेट से भरी हुई है| इस बाल्टी को भूमी पर खाली किया जाता है ओर इस रेट की एक शंक्वाकार धेरी बनाई जाती है| यदि शंकवाकार धेरी की ऊंचाई 24 सेमी है तो इस धेरी की त्रिज्या ओर तिर्यक ऊंचाई ज्ञात कीजिए|
View Solutionदो घनों, जिनमे से प्रत्येक का आयतन 343 घन सेमी है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है| इससे प्राप्त धनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए|
View Solutionदो घनों, जिनमे से प्रत्येक का आयतन 64 सेमी है, के संग्लग्न पालकों को मिलाकर एक ठोस बनाया जाता है| इससे प्राप्त धनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए|
View Solutionकोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यरोपित है| अर्धगोले का व्यास 14 सेमी है ओर इस बर्तन (पात्र) की कुल ऊंचाई 13 सेमी है| इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल तथा धारिता ज्ञात कीजिए|
View Solutionएक ठोस शंकु के आकार का है जो एक समान आधार त्रिज्या के अर्धगोले पर अध्यारोपित है| यदि अर्धगोले का वक्रपृष्ठ तथा शंकु का वक्रपृष्ठ समान हो तो शंकु की त्रिज्या ओर ऊंचाई का अनुपात ज्ञात कीजिए|
View Solutionएक खिलौना त्रिज्या 3.5 सेमी वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है| इस खिलौने की सम्पूर्ण ऊँचाई 15.5 सेमी है| इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए|
View Solutionसंलग्न आकृति में दर्शाया गया सजावट के लिए प्रयोग होने वाला ब्लॉक दो ठोसों से मिलकर बना है। इनमे से एक घन है ओर दूसरा अर्धगोला है इस ब्लॉक का आधार 5 सेमी कोर या किनारे वाला एक घन है ओर उसके ऊपर लगे हुए अर्धगोले का व्यास 4.2 सेमी है। इस ब्लॉक का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। `(pi = 22/7)` लीजिए|

View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ `1` सेमी है तथा शंकु को ऊंचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन ज्ञात कीजिए।
View Solutionएक बर्तन एक उलटे शंकु के आकार का है। इसकी ऊंचाई 8 सेमी है इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 सेमी है। यह ऊपर तक पानी से भरा है। जब इस बर्तन में सीसे की कुछ गोलियों जिनमे प्रत्येक 0.5 सेमी त्रिज्या वाला एक गोला है, डाली जाती है तो इसमें से भरे हुए पानी का एक-चौथाई भाग बाहर निकाय जाता है|। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
View Solutionएक जूस बेचने वाला अपने ग्राहकों को आकृति में दर्शाये गिलास से जूस देता था| बेलनाकार गिलास का आंतरिक व्यास 5 सेमी था, परन्तु गिलास के निचले आधार (तली) में एक उभरा हुआ अर्धगोला था, जिससे गिलास की धारिता कम हो जाती थी. यदि गिलास की ऊंचाई 10 सेमी थी, तो गिलास की आभासी धारिता तथा उसके वास्तविक धारिता ज्ञात कीजिए। `(pi = 3.14)` लीजिए।
View Solutionएक खोखले शंकु को आधार के समांतर किसी समतल द्वारा काटा जाता है ओर ऊपर के सिरे को हटा दिया जाता है| शेष भाग का वक्र पृष्ट सम्पूर्ण शंकु के वक्र परिष्ट्रीय क्षेत्रफल का `8/9` भाग है| ज्ञात कीजिए की शंकु किस ऊंचाई से काटा गया?
View Solutionत्रिज्या 8 सेमी ओर ऊंचाई 12 सेमी वाले एक शंकु को उसकी अक्ष के मध्य-बिंदु से होकर जाने वाले ओर आधार के समांतर तल द्वारा दो भागों में विभाजित किया जाता है| दोनों भागों के आयतनों का अनुपात ज्ञात कीजिए|
View Solution10 सेमी ऊंचाई ओर 6 सेमी आधार त्रिज्या के एक ठोस लम्ब वृत्तीय बेलन में से समान ऊंचाई ओर समान त्रिज्या वाला एक लम्ब वृतीय शंकु काट लिया जाता है| शेष बचे ठोस का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
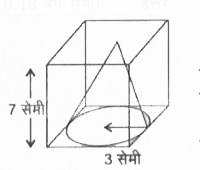
View Solutionभुजा 7 सेमी वाले एक ठोस घन में 7 सेमी ऊंचाई और 3 सेमी त्रिज्या वाले एक शंकु के आकार का छेद किया गया है| शेष ठोस का आयतन ज्ञात कीजिए|
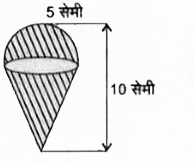
View Solutionसंलग्न आकृति में, एक आइसक्रीम शंकु दर्शया गया है, जिसमे आइसक्रीम भरी हुई है, तथा इनकी त्रिज्या 5 सेमी और ऊंचाई 10 सेमी है| आइसक्रीम का आयतन ज्ञात कीजिए, जबकि शंकु का `1/6` भाग आइसक्रीम में रिक्त रहता है|
View Solutionलकड़ी के एक ठोस बेलन के प्रत्ये सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा की आकृति में दर्शाया गया है। यदि बेलन की ऊंचाई 10 सेमी है और आधार की त्रिज्या 3.5 सेमी है तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

View Solutionएक धातु का गोला, जिसकी त्रिज्या 10.5 सेमी है, को पिघलाकर छोटे-छोटे शंकुओं में ढाला गया जिसमे से प्रत्येक की त्रिज्या 3.5 सेमी तथा ऊंचाई 3 सेमी है, ज्ञात कीजिए कुल कितने शंकु प्राप्त हुए|
View Solutionएक खोखला गोला जिसका आंतरिक और बाह्य व्यास क्रमश: 4.0 सेमी और 8.0 सेमी है, को पिघलाकर एक शंकु जिसके आधार का व्यास 8.0 सेमी है, बनाय जाता है| शंकु का वक्र पृष्ट ज्ञात कीजिए|
View Solutionएक ठोस खिलौना एक अर्धगोले के आकार का है जिस पर एक लंब वृत्तीय शंकु अध्यारोपित है। इस शंकु की ऊंचाई 2 सेमी है और आधार का व्यास 4 सेमी है। इस खिलौने का आयतन ज्ञात कीजिए।
View Solutionएक अर्धगोला और एक शंकु के समतल आधारों को जोड़कर एक ठोस निर्मित किया गया है। यदि ठोस का सम्पूर्ण आयतन `45 pi cm^(3)` और शंकु की ऊंचाई 9 सेमी है तो उभयनिष्ठ समतल का व्यास ज्ञात कीजिए।
View Solutionदवा का एक कैप्सूल बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्धगोला लगा हुआ है। संलग्न चित्र में कैप्सूल की लम्बाई `14` मिमी तथा व्यास `5` मिमी है| इसका सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

View Solutionएक ठोस बेलनाकार है जिसके दोनों सिरे अर्धगोलाकार है| ठोस की कुल उंचाई 20 सेमी है तथा बेलन का व्यास 7 सेमी है| ठोस का कुल आयतन और स्मपुर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए| (`pi=22/7` प्रयोग कीजिए)
View Solutionएक ठोस धातु के बेलन के दोनों सिरे अर्धगोलाकार है। इसकी सम्पूर्ण ऊंचाई 19 सेमी है तथा बेलन का व्यास 7 सेमी है। इस ठोस का आयतन और सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
View Solutionएक ठोस, एक बेलन के रूप में है जिसके दोनों सिरों पर अर्धगोले लगे हुए है। ठोस की कुल ऊंचाई 19 सेमी है और बेलन का व्यास 7 सेमी है। ठोस का भार ज्ञात कीजिए यदि 1 `cm^(3)` धातु का भार 4.5 ग्राम है। `(pi = 22/7)`
View Solution
लघु उत्तरीय प्रश्न्नोत्तर questions and complete solutions for chapter पृष्ठीय क्षेत्रफल और आयतन of UP BOARD PREVIOUS YEAR of Class 10