Complete Solutions to QUESTION BANK of chapter TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIGONOMETRY |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In the triangle shown, what is the perpendicular distance from the top vertex to the bottom side? What is the area of the triangle?
'(##VPU_TTT_MAT_X_P01_C05_E01_001_Q01##)'
View SolutionIn each of the following parallelograms, find the distance betwèen the top and bottom side? Calculate the area of each parallelogram.
'(##VPU_TTT_MAT_X_P01_C05_E01_002_Q01##)'
View SolutionA rectangular board is țo be cut along the diagonal and the pieces rearranged to form an equilateral triangle, and the sides of the triangle must. be 50 centimetres. What should be the length and breadth of the rectangle?
View SolutionTwo rectangles are cut along the diagorial and the triangles got are to be joined to another rectangle to make a regular hexagon as shown below:
'(##VPU_TTT_MAT_X_P01_C05_E01_004_Q01##)'
If the sides of the hexagón are 30 . centimetres, what would be the length and breadth of the rectangles?
View SolutionCalculate the area of the triangle shown.
'(##VPU_TTT_MAT_X_P01_C05_E01_005_Q01##)'
View SolutionThe diagonal of a square is '4 cm' long. Find
a) its perimeter?
b) its area?
View SolutionPQRS is a rectangle. Find angle SP R ? Find angle P RQ. If PR=30 then find P Qand QR . Calculate the perimeter of the rectangle.
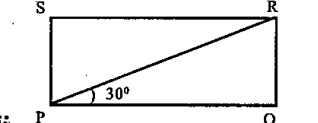
View SolutionCalculate the
a) perimeter and
b) area of the triangle
'(##VPU_TTT_MAT_X_P01_C05_E02_003_Q01##)'
View Solutionln `/_\ A B C, A B=10 cm, A C=8 cm`
`/_A=45^circ`
a) Find the perpendicular distance from `C` to `AB`.
b) Find the area of the triangle.
View SolutionCalculate the area of the triangle shown below.
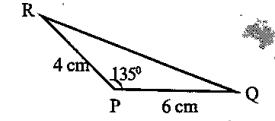
View SolutionWithout drawing pictures or looking up the tables, arrange the numbers 'sin `1^(circ)`,cos `1^(circ)`, sin `2^(circ)`, cos `2^(circ)`' in ascending order.
View SolutionThe lengths of two sides of a triangle are 8 cm and 10 cm and
the angle between them is `40^circ`. Calculate its area. What is
the area of the triangle with sides of the same Iength, but angle
between them `140^circ` ?
View SolutionThe sides of a rhombus are 5 centimetres Iong and one of its angles is `100^circ`Compute its area.
View SolutionThe sides of a parallelogram are 8 cm and 12 cm and
the angle between them is `50^circ`. Calculate its area.
View SolutionAngles of `50^circ` and `65^circ` are drawn at the end of a 5 cm
long line, to make a triangle. Calculate its area.
View SolutionA triangle is to be drawn with one side 8 cm and an angle on it `40^circ` .
What is the minimum length of the side opposite this angle ?
View SolutionThe diagonal of a square is '12 cm'. Calculate the perimeter and area of the square.
View SolutionThe length of the perpendicular drawn from a vertex to opposite side of an equilateral triangle is '12 cm'. Calculate its perimeter and area.
View SolutionOne side of a rhombus is 12 cm and one angle is `135^@`:- Find the distance between the parallel sides?
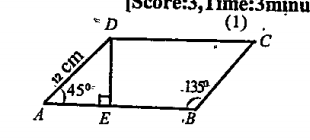
View Solutionln `/_\ A B C, /_ A=60^circ, /_B=45^circ, A B=10` cm
a) Find the perpendicular diśtance from C to `AB`.
b) Find the area of the triangle.
View SolutionIn the figure, BC =14, `/_B`=`40^@`,`/_C`=`50^@` Find the area of triangle ABC.
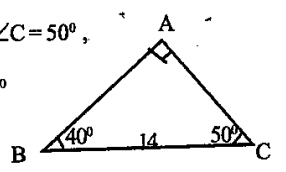
View SolutionThe figure shows a triangle and its circumcircle:
'(##VPU_TTT_MAT_X_P01_C05_E05_001_Q01##)'
What is the radius of the circle?
View SolutionWhat is the circum radius of an equilateral triangle of sides 8 centimetres?
View SolutionThe figure shows a triangle and its circum circle.
i) Compute the diameter of the circle.
ii) Compute the lengths of the other two sides of the triangle.
'(##VPU_TTT_MAT_X_P01_C05_E05_003_Q01##)'
View SolutionA circle is to. be drawn, passing through the ends of a line, 5 centimetres long, and the angle,on the circle on one side: of the line should be `80^(circ)` :
What should be the radius of the circle?
View SolutionIn the figure, O is the centre of the circle and `x^2+y^2=25` is the equation of the circle. What is the radius of the circle?
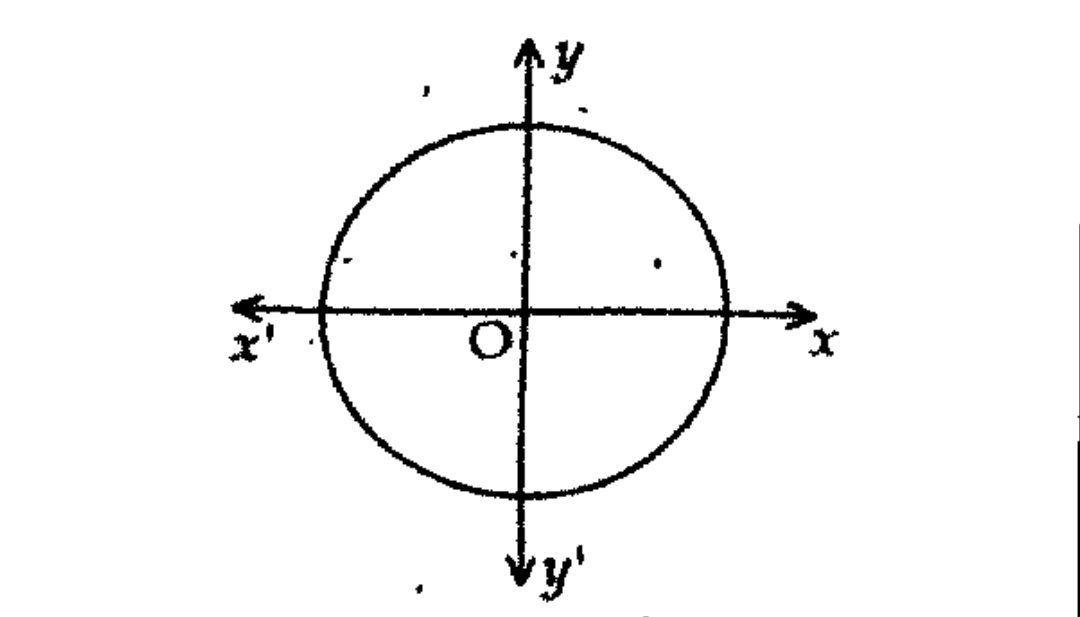 .
.
View SolutionA regular pentagon is drawn with vertices on a circle of radiús 15 centimetres. Calculate the length of its sides.
View SolutionThe figure shows a triangle and its circumcircle.
Compute the radius of the circle.
'(##VPU_TTT_MAT_X_P01_C05_E06_001_Q01##)'
View SolutionIn `triangle A B C, /_A=40 ^circ, B C=8 cm`
Find the circum diameter of the triangle. [sin '40=0.64]'
View Solutionln `triangle A B C , A B=7 cm, B C=12 cm, /_ B=40^circ`
a) Find the area of the triangle.
b) Calculate the length of AC.
View SolutionA B' is a chord of a circle with centre O.
'//_A O B=70^circ'
'A B=6 cm'. Find the diameter of the circle.
'[sin 35^circ=0.57]'
'(##VPU_TTT_MAT_X_P01_C05_E06_004_Q01##)'
View SolutionIn `/_\`ABC, `/_A =`125^@`,BC=8cm. Find the diameter of the circumcircle. [sin 55=.82]
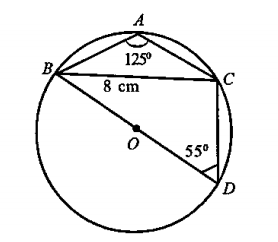
View SolutionOne ângle of a rhombus is `50^circ` and one diagonal
is 5 cm. What is its area?
View SolutionA ladder leans against a wall, with its foot 2 metres away
from the wall and the angle with the floor is `40^circ`. How
high is the top end of the ladder from the ground?
View SolutionThree rectangles are to be cut along the diagonals and the triangles so got rearrangedto form a regular pentagon, as shown in the picture. If the sides of the pentagon are to be 30 centimetres, what should be the length and breadth of the rectangles?
'(##VPU_TTT_MAT_X_P01_C05_E07_003_Q01##)'
View SolutionIn the picture, the vertical lines are equally spaced.
'(##VPU_TTT_MAT_X_P01_C05_E07_004_Q01##)'
Prove that their helghts are in arithmetic sequence.
What is the common difference?
View SolutionOne side of a triangle is 6 cm and the angle at its ends are `40^circ` and `65^circ`. Calculate its area.
View SolutionIn the figure 'B C=a, C D=b'
prove that 'a=3 b'
'(##VPU_TTT_MAT_X_P01_C05_E08_001_Q01##)'
View SolutionFind the area of a triangle whose sides are a and b and the angle between those sides is C
View Solutionln `/_\ A B C, A B=10 cm, /_ A=40^circ, /_B=70^circ'
`Compute the area of the triangle.
`[tan 40^circ=0.84 , tan 70=2.75]`
View SolutionAB' is the diameter of the circle. If 'PA=9' and '/_\ P A G=30^circ' find
a) Radius of the circle.
b) the lengths of the sides of the rilateral 'ADBC'.
'(##VPU_TTT_MAT_X_P01_C05_E08_004_Q01##)'
View SolutionA man `1.7`metres tall stands 10 metres away from the foot of a tree, and he sees the top of the tree at an angle of elevation `40^circ`. How tall is the tree?
View SolutionA man 1.8 metres tall looks down from the top of a light house 25 metres high and sees a ship at an angle of depression `35^circ` How far is the ship from the foot of the light house? Lets draw a figure first:
View SolutionA boy standing at the edge of a canal sees the top of a tree at an elevation of '70^circ .' 35^0Stepping 10 metres back, he sees It at an elevation of '25^circ'. The boy is 1.5 metres tall. How wide is the canal and how tall is the tree?
'(##VPU_TTT_MAT_X_P01_C05_E09_003_Q01##)'
View SolutionWhen the sun is at an elevation of `40^circ` the length of the
shadow of a tree is 18 metres. What is the height of the tree?
View SolutionWhen the sun is at an elevation of `35^circ`, the shadow of a tree is 10 metres. What would be the length of the shadow, when the sun is at an elevation of `25^circ` ?
View SolutionFrom the top of an electric post, two wires are stretched to either side and fixed to the ground, 25 meters apart. The wires make angle `55^circ`and `40^circ`with the ground. What is the height of the post?
View SolutionA '1.5' metre tall boy saw the top. of a building under construction at an elevation of `30^circ`.The completed building was 10 metres higher and the boy sáw its top at an elevation of `60^circ`from the same spot. What is the height of the büilding?
View SolutionA '1.75' metre tall man, standing at the foot of a tower, sees the top of a hill 40 metres away at an elevation of ' `60^o`Climbing to the top of the tower, he sees it at an elevation of `50^o`. Calculate the heights of the tower and the hill.
View SolutionA man `1.8` metre tall standing a the top of a telephonetower,
saw the top of a 10 m high building at a depression of `40^circ`
and the base of the building at a depression of `60^circ`. What is
the height of the tower? How far is it from the building?
View SolutionFind the relation of the perimeter and area of a,regular polygon with its, circumradius.
View SolutionFind a sequence of numbers getting. closer and closer to 'pi' using sin.
View Solutionln` /_\ A B C, A B=20 cm, A C=25 cm and /_ A=70^circ`
a) Find the perpendicular from C to A B.
b) What is the area of the triangle?
`[sin 70=0.94]`
View SolutionIn triangle PQR,
View SolutionIn '/_\ ABC, a, b, c' are the sides and 'R' be the circum radius, prove that the area of the triangle is '(abc)/( 4 R)'.
'(##VPU_TTT_MAT_X_P01_C05_E11_003_Q01##)'
View SolutionIn triangle 'ABC, /_\ A=90^circ' and tan 'B=2( 2/5)'
a) Find 'sin B, cos B'.
b) What is 'sin ^2 B+cos ^2 B ?'
'(##VPU_TTT_MAT_X_P01_C05_E11_004_Q01##)'
View SolutionIn `triangle ABC, AB=10 cm, AC=20 cm` and `/_ A=135^circ`
a) Compute the-area of the triangle.
View SolutionCharges `+2q, +q and +q` are placed at the corners A, B and C of an equilateral triangle ABC. If E is the electric field at the circumcentre O of the triangle, due to the charge `+q`, then the magnitude and direction of the resultant electric field at O is
View SolutionOne perpendicular side of a right triangle with angle `45^@` is '8 cm'.
a) What is the hypotensuse?
b) Find the radius from the midpoint of hypotenuse to the corner of the angle?
View SolutionA man observed the top of a tower at a distance `a` from its base
at an angle of elevation `30^circ`. He saw the top of a tower at an
angle of elevation `60^circ` from a point at the distance `b` from the
base, Prove that the height of the tower `h=sqrtab`
View SolutionWhen the sun is at an elevation of `40^circ` the shadow
of the flagpost is 15 metres.
a) Find the height of the flagpost.
b) What would be the length of, the shadow, when
the sun is at an elevation of `45^circ` ?
[tan 40=0.84 , sin 40=0.64]
View SolutionTwo buildings in a plane ground are 20 metres apart. From the top of the smaller building, one sees the base of the building at a depression of `50^circ`and its top at an elevation of`25^circ`.
a) Draw a rough figure and mark the measurements.
b) Find the helght of the smaller building.
c) Find the height of the bigger building.
'[tan 50^circ=1.2, tan 25^circ=0.4]'
View SolutionUsing the relations. " 'a//(sin A)=b/(sin B)=c/(sin C)=2 R' and 'A=1/2 a xx b sin C', prove.that area of a triangle 'A=(a b c)/(4 R)'.
View SolutionOne sees the top of a tree on the bank of a river at an elevation of `70^circ` from the other bank. Stepping 20 metres back, he sees the top. of the tree at an elevation of `55^circ`. Height of the person is '1.4' metres.
a) Draw a rough figure and mark the measurements.
b) Find the height of the tree.
c) Find the width of the river.
'[tan 70=2.75 , tan 55=1.43]'
View SolutionA tower is built in a river of width 80 metres. One sees the top of the river at an elevation of `55^circ` and`65^circ`. from either banks of the river.
a) Draw a figure using the given measurements.
b) Find the height of tower
c) Find the distances to either banks from the foot of the tower.
[tan `55^circ`=1.43 , tan `65^circ`=2.14]
View SolutionTwo children of same height standing on either sides of a tower, looks the top of tower at an elevation of `40^circ`, `55^circ`. The distance between the children is 25 metres. Height of the chlidren is 1.5 metres.
a) Draw a rough figure showing the givën measurements.
b) Calculate the height of the tower.
[sin `40^circ`=0.64, sin `55^circ`=0.82, cos `40^circ`=0.77, cos `55^circ`=0 .57, tan `40^circ`=0.89, tan `55^circ`=1.43]
View SolutionA child stands 30 metres away from the foot of a telephone tower, sees the top of the tower at an angle of elevation `30^circ`. Stepping some distance towards the tower, sees it at an elevation of `45^circ`
a) What is the height of the tower?
b) How much distance did he walk?
View SolutionOne sees a boat in the sea, on the top of a light house at a depression of `20^circ`. After sometimes he sees the boat at a depression of `30^circ`. If the height of the lighthouse is 160 meter. What distance will the boat travel during this time?
[tan 20=0.3640 , tan 30=0.5774]
View SolutionTwo buildings of same height in a plane ground are 80 meters apart, A boy standing in between sees the top of the buildings at an elevation of `35^circ` and `65^circ`.
a) Draw a rough figure.
b) Find the distaince from each buildings to the boy.
c) Find the height of büildings.
'[sin 35=0.57, cos 35=0: 81, tan 35=0.70 , sin 65=0.90, cos 65 .=0.42, tan 65=2.14]'
View SolutionOn the top of a 60 metre high building sees the top and
bottom of a tower at a depression of `30^circ` and `60^circ .`
What is the height of the tower?
View SolutionABCD is a parallelogram. 'AB=8 cm', 'A D=6 cm , /_\ D=120^circ .' Find the area of the parallelogram.
`(##VPU_TTT_MAT_X_P01_C05_E12_001_Q01##)`
View Solutionln `/_\ A B C, BC=18 cm, A C=18 cm` `/_C=120^circ`
(a) Find the perpendicular distance from 'C' to 'A B'.
b) What is the area of the triangle?
c) What is the ratio of sides of the triangle with angle `30^circ, 30^circ`and `120^circ ?`
View SolutionCan you cut out a triangle having one angle '37^circ' and side opposite to this angle as '9 cm' from a circular carboard sheet of radius '14 cm ?'
'[sin 37^circ=0.60, cos 37^circ=0.79]'
View SolutionIn triangle `ABC, AB=14 cm, AC=15cm, sin A=4/5 .` Find the following:
a) The perpendicular distance from C to AB.
b) The area of the triangle.
c) The length of BC.
View SolutionFrom the top of a building 15 meter high, one sees the top of another taller building at an angle of elevation of `70^circ` and bottom at an angle of depression of `40^circ`
a) Draw a rough figure and mark the measurements given.
b) Find the height of the taller building.
[ tan 70 = 2.747,tan40 = 0.839 ]
View SolutionIn triangle `/_\ABC`, AD is the median from A.`/_\BAD`=`35^circ`, AB=18 cm and AD= 12 cm. Find:
a) The ratio of the areas of the triangles `/_\ADC` and `/_\ABC`.
b) The perpendicular distance from D to AB.
c) The length of BC. [sin `35^circ`=0.57, cos `35^circ`=0.82, tan `35^circ`=0.7]
View SolutionIf in triangle 'ABC', 'A C=B C , /_\ A C B=80^circ' 'A B=8 cm', then compute the following.
'(##VPU_TTT_MAT_X_P01_C05_E12_007_Q01##)'
a) The perpendicular distance from C to 'AB'.
b) The area of triangle ABC.
c) The length of the sides 'A C' and 'B C'.
'[sin 80^circ=0.98, sin 50^circ=0.77, tan 80^circ= 5.67, tan 50^circ=1,19]'
View SolutionAngle measures of a triangle are '30^circ', '700^circ, 80^circ .' If the length of its smallest side is 10 centimetres, find the length of its other sides.
You can use the following table.
'(##VPU_TTT_MAT_X_P01_C05_E13_001_Q01##)'
View SolutionA boy standing on the top of a tower 20 metrés height, saw the top of a building at an elevation of `50^circ` and its base at a depression of `30^circ `
a) Draw a rough figure. according to the given data.
b) find the distance between the tower and the building.
c) find the distance from the top of the tower to the base of the building.
d) find the height of the building.
[sin `50^circ`=0.77, cos `50^circ`=0.64, tan `50^circ`=1.2, 'sqrt3`=1.7]
View SolutionA ladder leans against a wall. Its foot is 3 metres away from
the wall and making an angle `35^circ` with ground. How high is
the other end of the ladder from the ground?
`(sin 35^circ=0.57, cos 35^circ=0.82, tan 35^circ=0.70)`
View SolutionA boy sees the top of a tówer with an angle of elevation. `60^circ`.
Stepping 20metres back, he sees the same top with an angle
of elevation `30^circ`. Draw a rough figure and calculate
the height of the tower.
View SolutionIn the figure,
'/_\ B=90^circ, /_\ C=x^circ'
'/_\ A=y'
'(##VPU_TTT_MAT_X_P01_C05_E14_003_Q01##)'
a) What is 'x+y' ?
b) Prove that 'sin x=' 'cos y'
c) If 'sin x=cos x', find the vạalue of 'x'.
View SolutionIn the figure, '/_\ B=50^circ, /_\ ADC=135^circ' 'A B=10' centimetre. 'B C=25' centimetre.
`(##VPU_TTT_MAT_X_P01_C05_E14_004_Q01##)`
a) What is the area of the triangle 'ABC' ?
b) Find the length of DC.
'(sin 50^circ=0.77, cos 50^circ=0.64, tan 50^circ=1.19)'
View SolutionIn 'triangle A B C, /_\ A=75^circ, /_\ C=60^circ'
'(##VPU_TTT_MAT_X_P01_C05_E14_005_Q01##)'
a) What is the measure of '/_\ B ?'
b) If 'AB=5, sqrt2', what is the length of 'AC' ?
c) Find the ratio of 'AB: BC: AC'.
View SolutionIn triangle 'A B C', , the length of. AP, is 10 centimetres. What is the length of BP? What is the length of 'P C' ? Calculate the length of 'BC' ?
'(##VPU_TTT_MAT_X_P01_C05_E15_001_Q01##)'
View SolutionIn triangle 'ABC', length of 'AB=6 ~cm', '/_\ A=70^circ , /_\ B=55^circ'
'(##VPU_TTT_MAT_X_P01_C05_E15_002_Q01##)'
a) Find '/_\ C'.
b) Find 'AC'
c) Find the area of triangle 'ABC'. '(sin 70^circ=0.93)'
View SolutionA man standing on the top of a light house sees a ship approaching the seashore at an angle of depression of `22^circ`. After the ship has travelled 100 meters more towards the sea shore, he sees it at an angle of depression of `31^circ`.The ship stopes there.
a) Draw a rough-sketch.
b) How far is the ship from the light house.
c) Find the height of the light house.
(tan `22^circ`=0.4, tan `31^circ`=0.6)
View Solution'ABCD' is a parallelogram. 'AB=8 cm'. 'A D=4 cm, /_\ B=120^circ'
'(##VPU_TTT_MAT_X_P01_C05_E16_001_Q01##)'
a) What is '/_\ A' ?
b) What is the perpendicular distance from D to 'ABP^circ'
c) What is the area of ABCD?
View SolutionO is the centre of the circuń circle of triangle ABC.
'/_\ A=40^circ, /_\ B=80^circ'
'/_\ C=60^circ, B C=6.4' centimetres.
'(##VPU_TTT_MAT_X_P01_C05_E16_002_Q01##)'
a) What is the diametre of the circke.
b) What is the length of the other two sides.
View SolutionA boy saw the top of a building under construction at an elevation of `30^circ`.
The completed building was 12m higher and the boy saw its top, at an
elevation of `60^circ` from the same spot.
a) Draw a rough figure based on the given details.
b) What is the height of the building?
c) What is the distance between the building and the boy?
View SolutionIn the figure, 'C, D' are points on the circle 'AD' is a diameter of the circle '/_\ C=30^circ, A B=4' centimetres.
'(##VPU_TTT_MAT_X_P01_C05_E17_001_Q01##)'
a) '/_\ D=…….'
b) '/_\ A B D=……..'
c) What is the length of the diameter?
View SolutionIn triangle 'PQR, /_\ Q=90^circ, /_\ R=x^circ .' Lengths of the sides PQ, QR and PR are a, b, c respectively.
'(##VPU_TTT_MAT_X_P01_C05_E17_002_Q01##)'
a) Which among the following is 'tan x^circ ?' '(a/c, b/a, a/b, b/c)'
b) Similarly write 'sin x^circ' and 'cos x^circ' from this triangle:
c) Prove that '(sin x^circ)/(cos x^circ)=tan x'
View SolutionA boy is standing between two building of equal height. The boy and the buildings are in a straight line. He see the tops of those buildings at elevations of `45^o` and `30^o`. The nearest building is 20 metres away from him. Draw a rough figure.
View SolutionIn the figure
'/_\ B=90^circ'
'/_\ C=44^circ'
a) What is the measure of '/_\ A ?'
b) Which among the following is tan '44^circ' ?
'((A B)/(B C), (A B)/(A C), (B C)/(A B), (B C)/(A C))'
c) Prove that 'tan 44^circ xx tan 46^circ=1'.
'(##VPU_TTT_MAT_X_P01_C05_E18_001_Q01##)'
View SolutionIn the figure 'P' is the centre of the circle. 'A, B' and 'D' are points on the circle.
'/_\ P=90^circ, A D=5' centimetres.
'(##VPU_TTT_MAT_X_P01_C05_E18_002_Q01##)'
a) What is the measure of '/_\ A' ?
b) What is the area of triangle APD?
c) Find the area of the parallelogram ABCD.
View SolutionA boy standing at one bank of a river sees the top of a tree on the other bank directly opposite to the boy at an elevation of `60^o`. Stepping 40 metres back, he sees the top at an elevation of `30^o`. Draw a rough figure and find the height of the tree.
View SolutionDiagonal of a rectangle is 12 centimetres in length. The angle
made by the diagonal with one of its sides is `30^circ .` Find the
perimeter and area of the rectangle.
View SolutionIn triangle ABC if < B=`90^circ`, < A=`30^circ`, find sin C, cos C, tan C
View SolutionIn '/_\ ABC, /_A=125^circ, BC=8 cm', find diameter of the circle.
'(##VPU_TTT_MAT_X_P01_C05_E19_003_Q01##)'
View SolutionIn `/_\ ABC, AC=BC= 12` centimetres, < ACB=`60^circ`
a) What is the perpendicular distance from C to AB?
b) Calculate the area of the triangle.
View Solution
QUESTION BANK questions and complete solutions for chapter TRIGONOMETRY of V PUBLICATION of Class 10