Complete Solutions to QUESTION BANK of chapter GEOMETRY AND ALGEBRA of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | GEOMETRY AND ALGEBRA |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
What are the coordinates of the fourth vertex of the parallelogram shown below.
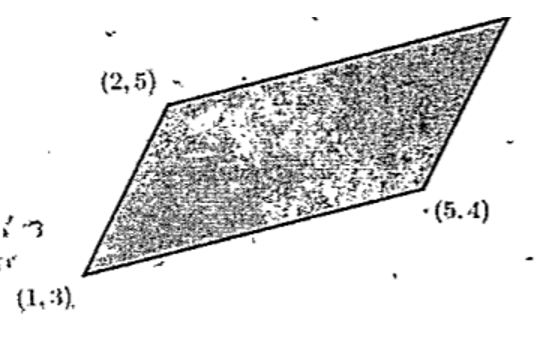
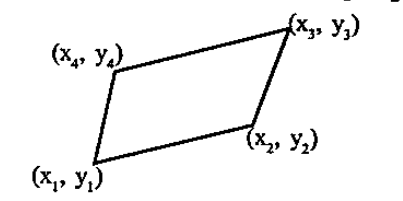
View SolutionThe figure shows a parallelogram with the coordinates of its vertices: Prove that `x_1+x_3=x_2+x_4andy_1+y_3=y_2+y_4`
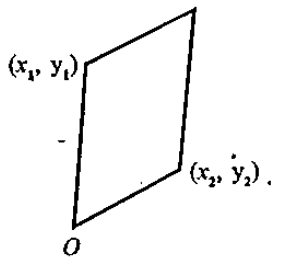
View SolutionA parallelogram is drawn with the lines joining `(x_1,y_1)and (x_2,y_2)` to the origin as adjacent sides."What are the coordinates of the fourth vertex?
View SolutionProve that in any parallelogram, the 'sum of the squares of all sides is equal to the sum of the squares of the diagonals'.
View SolutionIn this picture, the mid points of the sides of the large triangle are joined to make a small triangle inside.
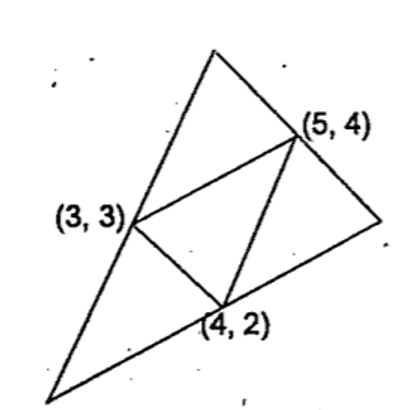
Calculate the co-ordínates of the vertices of the large triangle.
View SolutionA circle is drawn with the line joining '(2,3)' and '(6 , 5)' as diameter. What are the coordinates of the centre of the circle?
View SolutionThe coordinates of two opposite vertices of a parallelogram are '(4,5)' and '(1,3)'. What are the coordinates of the polnt of intersection of its diagonals?
View SolutionThe coordinates of the vertices of a quadrilateral taken in order are '(2,1)', '(5,3),(8,7),(4,9)'.
i) Find the coordinates of the midpoints of all four sides.
ii) Prove that the quadrilateral got by joining these mid points is a parallelogram.
View SolutionIn the picture, the mid points of the large rilateral are. joined to form the smaller rilateral within.
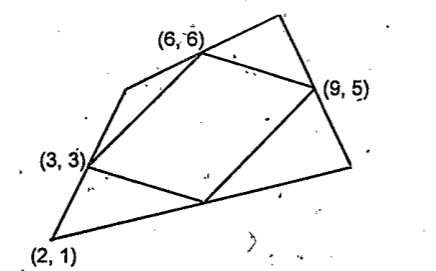
i) Find the coordinates of the fourth. vertex of the smaller rilateral.
ii) Find the coordinates of the other three vertices of the larger rilateral.
View SolutionThe coordinates of the vertices of a triangle are (3,5), (9,13), (10,6), Prove that this triangle is isosceles. Calculate its area.
View SolutionThe centre of a circle is '(1,2)' and a point on it is '(3,2)'. Find the coordinates of the other end of the diameter through thịs point.
View SolutionIf 'A(2,-1)' B '(3,4), C(-2,3)' are the vertices of a parallelogram find the fourth vertex.
View SolutionIn triangle 'ABC,(4,2)' is the mid point of 'AB'. The mid point of 'BC' is '(5,4)', the mid point of 'AC' is '(3,3)'
Draw a rough figure.
Find the vertices of the triangle.
View SolutionIf the points 'A(2,-2), B(14 , 10) C (11,13)' are the three vertices of a rectangle find the fourth vertex, 'D'.
View SolutionFind the coordinates of the midpoint of the line joining the points '(1,-2)', '(-3,4)'
View SolutionThe points 'A(6,1), B(8,2), C(9,4)', D '(p, 3)' are the vertices of a parallelogram.
Find the value of p using the concept that the diagonals of a parallelogram bisect each other
View SolutionOne end of the diameter of a circle is (1, 4). The center of the circle is '(3,-4)'.
Find the coordinates of the other end.
View SolutionCalculate the coordinates of the point dividing the line joining the points '(1,6)' and '(11,2)' in the ratio '3: 5'
View SolutionNow look at this pictüre:

The line inside the large triangle is the bisector of the top angle. We want to find the coordinates of the point where it meets the bottom side. That is we have to find the coordinates of 'D .'
View SolutionThe coordinates of two points 'A' and 'B' are '(3,2)' and '(8,7)'
Find the coordinates of:
i) the point 'P' on 'A B' with 'A P: P B=2: 3'
ii) the point 'Q' on 'A B' with 'A Q: Q B=3: 2'
View SolutionFind the coordinates of the points which divide the line joining '(1,6)' and '(5,2)' into three equal parts.
View SolutionThe coordinates of the vertices of a triangle are(-1,5),(3,7),(1,1).Find the coordinates of its centroid.
View SolutionCalculate the coordinates of the point P in the picture.
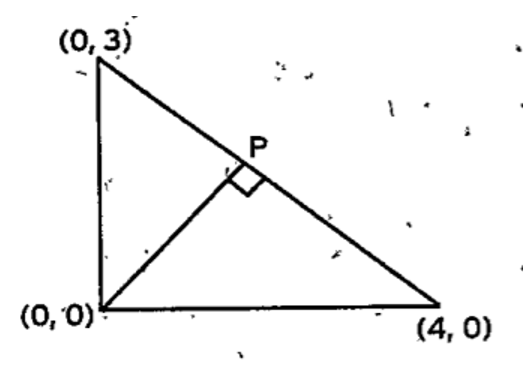
View SolutionFind the coordinates of the points 'P' and 'Q' which trisect the line joining '(2,-3)' and '(4,-1)'
View SolutionProve that A(6,4),B(5,-2),C(7,-2) is an isosceles triangle. If D is the mid point of the side BC ,find the coordinates of D. Calculate the length of this median. Also find the coordinates of centroid.
View SolutionFind the coordinates of the point which divides the line joining '(4,-3),(9,7)' in the ratio '3: 4'.
View SolutionIn `Delta` ABC A(6,8),B(3,4),C(-2,2) are its vertices. The bisector of `/_A` cuts BC at D. Find BD:CD.
View SolutionProve that the points '(1,3),(2,5)' '(3,7)' are on the same line.
View SolutionFind the coordinates of two more points on the line joining '(-1,4)' and '(1,2)'.
View Solution`x_1, x_2 , x_3` and `y_1, y_2, y_3 ……..` are arithmetic sequences. Prove that all points with coordinates in the sequence `(x_1, y_1),(x_2, y_2),(x_3, y_3), ………...` of number pairs are on the same line.
View SolutionProve that if the points `(x_1, y_1),(x_2, y_2), (x_3, y_3)` are on a single line, then the points `(3 x_1+2 y_1, 3 x_1-2 y_1),(3 x_2+2 y_2, 3 x_2-2 y_2)` `(3 x_3+2 y_3, 3 x_3-2 y_3)` are also on a single line. Would this be true if we take some other numbers instead of `3` and `2` ?
View SolutionFind the equation of the line joining (1,2) and (2,4), For points on this line with the consecutive natural numbers '3,4,5, '……...as the 'x' coordinates, what is the sequence of y coordinates?
View SolutionFind the equation of the line joining (-1,3) and (2,5).Prove that if the point (x,y)is on this line,so is the point (x+3,y+2).
View SolutionProve that whatever number we take as x,the point (x,2x+3) is a point on the line joining (-1,1) and (2, 7).
View SolutionIn the picture below, the x coordinate of a point on the slanted (blue) line is 3.
i) What is its y coordinate?
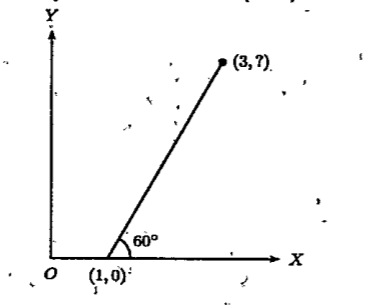
ii) What is the slope of the line?
iii) Write the equation of the line.
View SolutionIn the picture here, 'ABCD' 'is a square. Prove that for any point on the diagonal 'BD', the sum of the 'x' and ' y' coordinates is zero.

View SolutionProve that for any point on the line intersecting the axes in the picture, the sum of the 'x' and 'y' coordinates is 3 .

View SolutionFind the equation of the circle with centre at the origin and radius '5 .' Write the coordinates of eight points on this circle.
View SolutionProve that if '(x, y)' be a point on the circle with the line joining '(0,1)' and '(2,3)' as diameter, then 'x^2+y^2-2 x-4 y+' '3=0'. Find the coordinates of the points where this circle cuts the 'y' axis:
View SolutionWhat is the equation of the circle shown below?
'(##VPU_TTT_MAT_X_P02_C09_E07_009_Q01##)'
View SolutionWhat are the coordinates of the centroid of the triangle with vertices `(x_1,y_1)` `(x_2,y_2)` and`(x_3,y_3)`
View SolutionWe have seen that the points (3,5),(6,7),(9,9) are points on the same line. is there any relation between the 'x' coordinates 3,6 .and 9 of these points? What about the y coordinates 5,7,9 ? Can you find some more points on this line with natural number coordinates?
View SolutionProve that the quadrilateral formed by joining the points '(-1,-1),(6,6),(5,7)' '(-2,6)' is cyclic.
View Solution(7,10)' is a point on the circle centred at '(1,2) .' Find the length of the tangent from the point '(-25,2)' to the circle.
View SolutionIf a circle is drawn with centre as origin and radius 2, then how many points has on the circle in which 'x' and 'y' co ordinatés are integers. Iś the centre '(2 , 3) ?' What about the points in which any co ordinate is an integer?
'(##VPU_TTT_MAT_X_P02_C09_E08_003_Q01##)'
View SolutionProve that for all points on the line joining the origin and the point (4,2), the 'x' -coordinate is dơuble the 'y-' coordinate. What is the equation of this line?
View SolutionWhat is the equation of the line joining the points '(1,3),(2,7) ?' Prove that if '(x, y)' is a point on this line, so is the point '(x+1, y+4)'
View SolutionWhat is the point at which the line `2 x+ 4 y-1=0` cuts
the `x` -axis? What about the `y` - axis?
View SolutionProve that the equations `3 x+2 y+5=0` and `3 x+2 y-1=0` are parallel.
What are the points of the lines cut the `x` -axis? What about the y-axis?
View Solutiona) If 'C(-1, k)' is a point on the line passing through the point 'A(2,4)' and 'B(4,8)' which number is 'K' ?
b) What is the relation between the 'x' coordinate and the y.coordinate of any point on this line?
View SolutionC' is the centre of the circle passing through the origin. Circle cúts the 'y' axis at 'A(0,4)' and the axis at 'B(4,0)'.
a) Write coordinates of C.
b) Write the equation of the circle.
c) '(0,0)' is a point on the circle. There is one more point on the circle with. 'x' and y coordinates'equal. Which is that point?
View SolutionA circle is drawn with the origin as centre. It passes through
the point `(3,3)`
a) What is the radius of the circle?
b) Write the coordinates of a point where the circle meets
the `X` - axis.
View SolutionThe coordinates of the vertices of a triangle are 'A(1,1), B(5,5) , C(2,5)'
a), Write the coordinates of the midpoint D of AB.
b) What is the length of CD?
c) What are the coordinates of the point dividing the line 'CD' in the ratio '2: 1 ?'
View SolutionA circle with centre '(3,4)' passes through the origin.
a) What is the radius of the circle.
b) If a point on the circle is '(x, y)', write the relation between 'x, y'.
c) Check whether the point '(-2,1)', lies on this circle.
View SolutionFind the slope of the line joining '(2,4)' and '(4,7)'. Write the coordinates of another point on this line. Check whether '(5,8)' is on this line.
View SolutionFind the length of line joining 'A(-2,-3)' and 'B(4,5)'. write the equation of circle whose diameter is 'AB'.
View SolutionA triangle has its vertices 'A(3,2) , B(-5,-4)', 'C(7,8) . P, Q, R' are the midpoints of 'AB', 'BC' and 'AC' respectively.
a) Find the coordinates of 'P, Q' and 'R'.
b) Find the perimeter of `/_\ PQR`.
View SolutionA(1,2) , B(7,3), C(8,9) are the vertices of a parallelogram ABCD.
Find the coordinates of 'D'.
View SolutionA(1,2) , B(7,4), C(5,10)' are the vertices of /_\ ABC'. Also 'P, Q',and 'R' are the midpoints of 'AB, BC' and 'AC' respectively.
a) Find the coordinates of 'P, Q' and 'R'.
b) Prove that 'Delta P Q R' is angled.
View SolutionA(-2,3) , B(6,9)' be two points
a) Find the coordinates of the centre of the circle with diameter 'AB'. Compute the diameter.
b) If 'C' and 'D' are '(-3,5)' and '(5,-1)'. Justify whether 'CD' is a diameter?
c) If 'P' and 'Q' are '(5,10)' and '(-1,2)'. Justify whether 'PQ' is a diameter?
View SolutionThe sum of the 'x' coordinates of the points where the line cut 'x' axis is 14
If (3,4) is a point on it, find the equation of the line.
View Solution
QUESTION BANK questions and complete solutions for chapter GEOMETRY AND ALGEBRA of V PUBLICATION of Class 10