Complete Solutions to Creative Bits for CCE Model Examination of chapter POLYNOMIALS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | POLYNOMIALS |
| VGS PUBLICATION-BRILLIANT | Creative Bits for CCE Model Examination |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A quadratic polynomial whose zeroes are 5 and -2 is
View SolutionIf y = p(x) is represented by the given graph, then the number of zeroes are
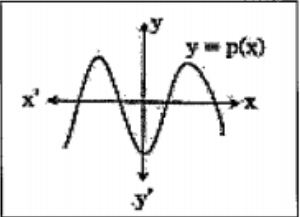
View SolutionIf `sqrt(3)` and `-sqrt(3)` are the zeroes of a polynominal p(x), then p(x) is
View SolutionThe quadratic polynomial whose zeroes are `sqrt(15)` and `-sqrt(15)` is
View SolutionIf one zero of the quadratic polynomial `2x^(2) + kx - 15` is 3, then the other zero is
View SolutionThe maximum number of zeroes that a polynomial of degree 3 can have is
View SolutionThe product and sum of the zeroes of the quadratic polynomial `ax^(2) + bx +c` respectively are
View SolutionThe number of zeroes of the polynomial function p(x) whose graph is given below is

View SolutionThe zeroes of the polynomial `p(x) = 4x^(2) - 12x +9` are
View SolutionIf `alpha` and `beta` are zeroes of the polynomial `p(x) = x^(2) - 5x +6`, then the value of `alpha + beta - 3 alpha beta` is
View SolutionThe graph of the polynomial `f(x) = 2x - 5` is a straight line which intersects the X - axis at exactly one point namely.
View SolutionIf 1 is the zero of the quadratic polynomial `x^(2) + kx -5` , then the value of k is
View SolutionThe number of zeroes lying between -2 and 2 of the polynomial f(x) whose graph is given below is
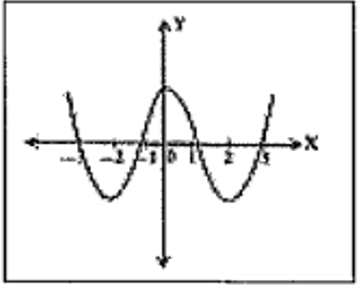
View SolutionIf both the zeroes of a quadratic polynomial `ax^(2) + bx + c` are equal and opposite in sign, then b is
View SolutionSum and product of the zeroes of polynomial `x^(2) - 3` are respectively.
View SolutionIf the zeroes of quadratic polynomial are equal in magnitude but opposite in sign, then
View SolutionIf one of the zeroes of the quadratic polynomial `ax^(2) + bx + c` is 0, then the other zero is
View SolutionThe polynomial whose zero are -5 and 4 is
View SolutionIf -1 is a zero of the polynomial `f(x) = x^(2) - 7x -8`, then the other zero is
View SolutionIf one zero of the quadratic polynomial `x^(2) - 5x -6` is 6, then the other zero is
View SolutionIf `alpha` and `beta` are the zeros of the polynomial `f(x) = x^(2) + px + q` , then a polynomial having `1/(alpha)` and `1/beta` as its zeros is …………..
View SolutionIf `f(x)=ax^2+bx+c` has no real zeros and a+b+c<0 then…..
View SolutionIf `alpha, beta, gamma` are the zeros of the polynomial `f(x) = ax^(3) + bx^(2) + cx + d` then `1/(alpha) + 1/(beta) + 1/(gamma)` = ………….
View SolutionIf the product of zeros of the polynomial `f(x)=a x^3-6x^2+11 x-6` is 4, then `a=` (a) `3/2` (b) `-3/2` (c) `2/3` (d) `-2/3`
View SolutionIf the order of `ax^(5) + 3x^(4) + 4x^(3) + 3x^(2) + 2x +1` is 4 then a = …………..
View SolutionIf one zero of the polynomial `f(x) = 5x^(2) + 13x + k` is reciprocal of the other , then the value of k= ……….
View SolutionIf `alpha, beta` are the zeros of polynomial `f(x) = x^(2) - p(x+1)-c` then `(alpha + 1) (beta +1 )` = …………
View SolutionIf the sum of the zeros of the polynomial `f(x) = 2x^(3) - 3 kx^(2) + 4x - 5` is 6 then k = …………
View SolutionIf `alpha, beta, gamma` are the zeros of the polynomial `f(x) = ax^(3) + bx^(2) + cx + d` then `(alpha)^2 + (beta)^2 + (gamma)^2` = ………….
View SolutionIf the polynomial `f(x) = ax^(3) + bx - c` is divisible by the polynomial `g(x) = x^(2) + bx + c` then ab = …………..
View SolutionThe product of the zeros of `x^(3) + 4x^(2) + x - 6` is ………….
View SolutionA quadratic polynomial , the sum of whose zeroes of 0 and one zero is 3 is ……………
View SolutionIf `sqrt(5)` and `-sqrt(5)` are two zeros of the polynomial `x^(3) + 3x^(2) - 5x -15` then its third zero is …………..
View SolutionIf `alpha, beta , gamma` are the zeros of the polynomial `x^(3) - px^(2) + qx - r` then `1/(alpha beta) + 1/(beta gamma) + 1/(gamma alpha)` = …………..
View SolutionIf `x+ 2` is a factor of `x^(2) + ax + 2b` and `a+b = 4` then a = …………..
View SolutionIn the above problem b = ……………..
View SolutionIf one zero of the polynomial `f(x) = (k^(2)+4)x^(2) + 13 x + 4k` is reciprocal of the other then k = ………..
View SolutionIf two zeros of `x^(3) + x^(2) - 5x -5` are `sqrt(5)` and `-sqrt(5)` then its third zero is …………….
View SolutionIf zeros of polynomial `f(x0 = x^(3) - 3px^(2)+qx-r` are in AP then `2p^(3)` = ………..
View SolutionIf `alpha, beta` are the zeros of the polynomial `f(x) = ax^(2) + bx + c` then `1/(alpha^2) + 1/(beta^2)` = …………….
View SolutionWhat should be subtracted from the polynomial `x^(2) - 16x + 30` so that 15 is the zero of the resulting polynomial?
View SolutionFrom the graph the number of zeros of the polynomial is ………………

View SolutionThe number of zeros of the polynomial in the graph is …………

View SolutionThe number of zeros of the polynomial in the graph is ………….

View SolutionThe below graph represents
View SolutionThe graph represents …………..
View Solution`ax + b` represents ………… polynomial.
View Solution`ax^(2) + bx + c` is a …………… polynomial.
View SolutionWhich of the following is a cubic polynomial in general form?
View SolutionThe degree of the polynomial `ax^(4) + bx^(3) + cx^(2) + dx + e` is ………..
View Solution`a_(0)x^(n) + a_(1)x^(n-1) + a_(2)x^(n-2) + ……..a_(n)x^(n)` is polynomial of degree ……………
View SolutionIf a>0 then the shape of `ax^2+bx+c=0` is ……
View SolutionIf a<0 then the shape of `ax^2+bx+c=0` is ,……..
View SolutionIf `alpha , beta , gamma` are roots of a cubic polynomial `alpha + beta + gamma` = ……………..
View SolutionIf `alpha, beta, gamma` are roots of a cubic polynomial then `alpha beta + beta gamma + gamma alpha` = …………….
View Solution" Every quadratic polynomial will have 2 zeros". This is ………….
View Solution`f(x) = 3x - 2` then zero of f(x) is …………
View Solution`p(t) = t^(3) - 1 , p(-2)` = ………….
View Solution`p(x) = x^(2) + 5x + 6` then zeros of p(x) = …………..
View Solution`p(x) = 4x^(2) + 3x -1` then `p(1/4)` = ……..
View Solution`x^(2) + 7x+10`= ………..
View Solution`p(x) = x^(3) + 4x^(2) + 5x -2` then p(1) = ……………
View Solution`p(x) = 3x^(3) - 2x^(2) + 6x - 5` then p(2) = ………………
View SolutionIf m and n zeros of the polynomial `3x^(2) + 11x -4` then the value of `m/n + n/m` = ………………
View SolutionSum of the zeros of `x^(2) + 7x + 10` is …………….
View SolutionThe quadratic polynomial, whose sum and product of zeros are 1 and -2 respectively is ……………
View SolutionIf p and q are the zeros of the polynomial `t^(2) - 4t + 3` then `1/p + 1/q - 2pq + 14/3 = ………….`
View SolutionA polynomial of degree 3 is called ……………. Polynomial.
View SolutionThe quotient when `x^(4)+ x^(3) + x^(2) - 2x - 3` is divided by `x^(2) -2` is ……………….
View SolutionDivide `(x^(3)-6x^(2)+11x-12)` by `(x^(2)-x+2)` then quotient is …………..
In the above problem the remainder is
View SolutionOne zero of the polynomial `2x^(2) + 3x + k is 1/2` then k = ……………..
View SolutionIn the above problem other zero is …………
View SolutionSum of the zeros of `6x^(2) = 1` is ……………
View SolutionWhat must be subtracted or added to `p(x) = 8x^(4) + 14x^(3)-2x^(2) + 8x -12` so that `4x^(2) + 3x - 2` is a factor of p(x)?
View SolutionThe quadratic polynomial whose zeroes are `4+sqrt(5)` and `4-sqrt(5)` is ………….
View SolutionIf one of the zeros of the quadratic polynomial `f(x) = 14x^(2) -42k^(2)x-9` is negative of the other then k = ………………
View SolutionIf one zero of a polynomial `3x^(2) -8x + 2k +1 = 0` is seven times the other then k = …………….
View SolutionIf `2x + 3` is a factor of `2x^(3) - x - b + 9x^(2)` then the value of b is ……………
View SolutionDivide `(x^(3)-6x^(2)+11x-12)` by `(x^(2)-x+2)` then quotient is …………..
View SolutionIn the above problem remainder is …………….
View SolutionIf `alpha` and `beta` are the zeros of the polynomial `p(x) = 2x^(2) + 5x + k` satishfying the relation `alpha^(2) + beta^(2) + alpha beta = 21/4` then k = …………
View Solution`(x - sqrt(5/3))(x+sqrt(5/3)) = ……………`
View SolutionProduct of zeros of `3x^(2) = 1` is ………..
View SolutionDegree of '1' is …………
View SolutionDegree of `5x^(7) - 6x^(5) + 7x + 1` is ……….
View Solution`(3x-4)(x+1)`= ………..
View Solution`(x^(2) -3x - 28) -: (x+4)` = ………..
View Solution`f(x) = 4x^(2)+4x-3` then `f((-3)/2)` = ………..
View SolutionIn the above problem `f(1/2) = ………….`
View Solution`(x+sqrt(5))(x-3sqrt(5))=……….`
View Solution`(-x^(3)+3x^(2)-3x+5)-:(-x^(2)+x-1)` = …………..
View SolutionThe remainder when `3x^(3) + x^(2) + 2x + 5` is divided by `x^(2) + 2x + 1` is ………….
View Solution`alpha = a - b, beta = a+b` then the quadratic polynomial is ……………..
View SolutionIf the product of zeros of `9x^(2)+3x+p` is 7 then p ……….
View SolutionDegree of `(x-2)(x-3)` is ……….
View SolutionThe value of `x^(15) - 1` at x = 0 is ……………….
View SolutionZeros of the polynomial `x^(2) - 4x + 3` and 1 and p the p = ………………
View SolutionDegree of a linear polynomial is ……………….
View Solution`(a+1)^(2)`= ……………
View Solution`alpha + beta = 0, alpha beta = sqrt(3)` then the quadratic polynomial is ……………
View Solution
Creative Bits for CCE Model Examination questions and complete solutions for chapter POLYNOMIALS of VGS BRILLIANT MATHS (TELUGU ENGLISH) of Class 10
All Exercises from VGS PUBLICATION-BRILLIANT Class 10 MATHS POLYNOMIALS
- Creative Bits for CCE Model Examination
- Creative Questions for CCE Model Examination
- Do These
- Do This
- Examples
- EXERCISE
- Exercise 3.1
- Exercise 3.2
- Exercise 3.3
- Exercise 3.4
- Optional exercise
- Part - B : Observation bits to solve various bits given in the public examination.
- Part -A : Observation Material to solve various questions given in the public examination ( 1 Mark Questions)
- Part -A : Observation Material to solve various questions given in the public examination ( 2 Mark Questions)
- Part -A : Observation Material to solve various questions given in the public examination ( 4 Mark Questions)
- Try These
- Try This