Complete Solutions to EXERCISE of chapter QUADRATIC EQUATIONS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | QUADRATIC EQUATIONS |
| VGS PUBLICATION-BRILLIANT | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Check whether the following equations are quadratic or not.
`x^(2) - 6x - 4 = 0`
View SolutionCheck whether the following equations are quadratic or not.
`x^(3) - 6x^(2) + 2x -1 = 0`
View SolutionCheck whether the following equations are quadratic or not.
`7x = 2x^(2)`
View SolutionCheck whether the following equations are quadratic or not.
`x^(2) + 1/x^(2) = 2`
View SolutionCheck whether the following equations are quadratic or not.
`(2x + 1) (3x + 1) = 6(x - 1)(x - 2)`
View SolutionCheck whether the following equations are quadratic or not.
`3y^(2) = 192`
View SolutionRepresent the following situations mathematically :
Raju and Rajender together have 45 marbles. Both of then lost 5 marbles each. And the product of the number of marbles now they have is 124.
View SolutionRepresent the following situations with suitable mathematical equations.
The hypotenuse of a right triangle is 25 cm. We know that the difference in lengths of the other two sides is 5 cm. We would like to find out the length of the two sides?
View SolutionCheck whether the following are quadratic equations:
`(x - 2)^(2) + 1 = 2x - 3`
View SolutionCheck whether the following are quadratic equation:
`x(x+1)+8=(x+2)(x-2)`
View SolutionCheck whether the following are quadratic equation:
`x(2x+3)=x^(2)+1`
View SolutionCheck whether the following are quadratic equation:
`(x+2)^(3)=x^(3)-4`
View SolutionCheck whether the following are quadratic equations:
`(x + 1)^(2) = 2(x - 3)`
View SolutionChek whether the following are quadratic equation:
`x^(2)-2x=(-2)(3-x)`
View SolutionChek whether the following are quadratic equation:
`(x-2)(x+1)=(x-1)(x+3)`
View SolutionChek whether the following are quadratic equation:
`(x-3)(2x+1)=x(x+5)`
View SolutionChek whether the following are quadratic equation:
`(2x-1)(x-3)=(x+5)(x-1)`
View SolutionChek whether the following are quadratic equation:
`x^(2)+3x+1=(x-2)^(2)`
View SolutionChek whether the following are quadratic equation:
`(x+2)^(3)=2x(x^(2)-1)`
View SolutionChek whether the following are quadratic equation:
`x^(3)-4x^(2)-x+1=(x-2)^(3)`
View SolutionRepresent the following situations in the form of quadratic equation:
The area of a rectangular plot is 528 `m^(2)`. The length of the plot is one metre more than twice its breadth. We need to find the length and breadth of the plot.
View SolutionThe product of two consecutive positive integers is 306. We need to find the integers.
View SolutionRepresent the following situations in the form of quadratic equation:
Rohan’s mother is 26 years older than him. The product of their ages after 3 years will be 360 years. We need to find Rohan’s present age
View SolutionA train travels a distance of 480 km at a uniform speed. If the speed had been 8km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
View SolutionFind the roots of the equation using factorisation method.
`x^(2)+5x+6=0`
View SolutionFind the roots of the equation using factorisation method.
`x^(2)-5x+6=0`
View SolutionFind the roots of the equation using factorisation method.
`x^(2)+5x-6=0`
View SolutionFind the roots of the equation using factorisation method.
`x^(2)-5x-6=0`
View SolutionVerify that 1 and `3/2` are the roots of the equation `2x^(2) - 5x + 3 = 0.`
View SolutionFind the roots of the equation `2x^(2) - 5x + 3 = 0` by factorisation.
View SolutionFind the roots of the quadratic equation `x - 1/(3x) = 1/6`
View SolutionThe altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
View SolutionA cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs. 90, find the number of articles produced and the cost of each article.
View SolutionFind the dimensions of a rectangle whose perimeter is 28 meters. And whose area is 40 square meters.
View SolutionThe base of a triangle is 4cm longer than its altitude. If the area of the triangle is 48 sq.cm, then find its base and altitude.
View SolutionTwo trains leave a railway station at the same time. The first train travels towards west and the second train towards north. The first train travels 5 km/hr faster then the second train. If after two hours they are 50 km. apart, find the average speed of each train.
View SolutionIn a class of 60 students, each boy contributed rupees equal to the number of girls and each girl contributed rupees equal to the number of boys. If the total money then collected was Rs. 1600, how many boys are there in the class?
View SolutionA motor boat heads upstream a distance of 24km on a river whose current is running at 3km per hours. Assuming that the motor boat maintained a constant speed, what was its speed ?
View SolutionSolve the equations by completing the square.
`x^(2) - 10x + 9 = 0`
View SolutionSolve the equations by completing the square
`x^(2) - 5x + 5 = 0`
View SolutionSolve the equations by completing the square
`x^(2) + 7x - 6 = 0`
View SolutionIf one can induce parthenocarpy through the application of growth substances, which fruits would you select to induce parthenocarpy and why?
View SolutionFind the roots of the equation `5x^(2) - 6x - 2 = 0` by the method of completing the square.
View SolutionFind the roots of `4x^(2) + 3x + 5 = 0` by the method of completing the square.
View SolutionThe two consecutive positive odd integers such that the sum of their squares is 290 are
View SolutionA rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the reatangular park and of altitude 12m. Find its length and breadth.
View SolutionFind the roots of the following quadratic equations, if they exist.
`x^(2)+4x+5=0`
View SolutionFind the roots of the following quadratic equations, if they exist.
`2x^(2)-2sqrt(2)x+1=0`
View SolutionFind the roots of the following equations:
`x + 1/x = 3, x ne 0`
View SolutionFind the roots of the following equations:
`1/x - 1/(x - 2) = 3 , x ne 0, 2`
View SolutionA motor boat whose speed is 18km/h in still water. It takes 1 hour more to go 24km upstream than to return downstream to the same spot. Find the speed of the stream.
View SolutionFind the roots of the following quadratic equations, if they exist.
`2x^(2)+x-4=0`
View SolutionFind the roots of the following quadratic equations, if they exist.
`4x^(2)+4sqrt(3)x+3=0`
View SolutionFind the roots of the following quadratic equations, if they exist.
`5x^(2)-7x-6=0`
View SolutionFind the roots of the following quadratic equations, if they exist.
`x^(2)+5=-6x`
View SolutionFind the roots of the quadratic equation by applying the quadratic formula.
`2x^(2) + x - 4 = 0`
View SolutionFind the roots of the quadratic equation by applying the quadratic formula.
`4x^(2) + 4 sqrt3 x + 3 = 0`
View SolutionFind the roots of the quadratic equation by applying the quadratic formula.
`5x^(2) - 7x - 6 = 0`
View SolutionFind the roots of the quadratic equation by applying the quadratic formula.
`x^(2) + 5 = -6x`
View SolutionFind the roots of the following equations:
`x-(1)/(x)=3, x ne 0`
View SolutionFind the roots of the following equations :
`1/(x + 4) - 1/(x -7) = 11/30 , x ne -4,7`
View SolutionThe sum of the reciprocals of Rehman ages, (in years) 3 years ago and 5 year from now is `1/3` Find his present age.
View SolutionIn a class test, the sum of Moulika’s marks in Mathematics and English is 30. If she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in the two subjects.
View SolutionThe diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more then the shorter side, find the sides of the field.
View SolutionThe difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number.Find the two numbers.
View SolutionA train travels 360 km at a uniform speed. If the speed had been 5 km/h more, if would have taken 1 hour less for the same journey. Find the speed of the train.
View SolutionTwo water taps together can fill a tank in `9 3/8` hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
View SolutionAn express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more then that of the passenger train, find the average speed of the two trains.
View SolutionSum of the areas of two squares is 468 `m^(2)` If the difference of their perimeters is 24m, find the sides of the two squares.
View SolutionSum of the areas of two squares is 468 `m^(2)`. If the difference of their perimeters is 24 m, find the sides of the two squares.
View SolutionA stone is thrown vertically upwards with an initial velocity of `10ms^(-1)` from the top of a cliff of height 40m.How much time it take to reach the ground?
View SolutionIf a polygon of 'n' sides has `1/2 n (n - 3)` diagonals. How many sides will a polygon having 65 diagonals ? Is there a polygon with 50 diagonals?
View SolutionFind the discriminant of the quadratic equation`2x^(2) - 4x + 3 = 0`and hence find the nature of its roots.
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so ? If yes, at what distances from the two gates should the pole be erected ?
View SolutionFind the discriminant of the equation `3x^(2) - 2x + 1/3 = 0` and hence find the nature of roots. Find them, If they are real.
View SolutionExplain the benefits of evaluating the discriminant of a quadratic equation before attempting to solve it. What does its value signifies?
View SolutionWrite three quadratic equations one having two distinct real solutions, one having no real solution and one having exactly one real solution.
View SolutionFind the nature of the roots of the following quadratic equations. If real roots exist, find them.
`2x^(2) - 3x + 5 = 0`
View SolutionFind the nature of the roots of the following quadratic equations. If real roots exist, find them.
`3x^(2) - 4 sqrt 3x + 4 = 0`
View SolutionFind the nature of the roots of the following quadratic equations. If real roots exist, find them.
`2x^(2) - 6x + 3 = 0`
View SolutionFind the values of k for each of the following quadratic equations, so that they have two equal roots. `2x^2+kx+3=0`
View SolutionFind the values of k for each of the quadratic equations, so that they have two equal roots.
`kx(x-2)+6=0 (k ne 0)`
View SolutionIs it possible to desigh a rectangular mango grove whose length is twice its breadth, and the area is 800 `m^(2)` ? If so find its length and breadth.
View SolutionThe sum of the ages of two friends is 20 years. Four years ago,the product of their ages in years was 48. Is the above situation possible ? If so, determine their present ages
View SolutionIs it possible to desigh a rectangular park of perimeter 80m and area `400m^(2)` ? If so, find its length and breadth.
View SolutionSome points are plotted on a plane. Each point is joined with all remaining points by line segments. Find the number of points if the number of line segments are 15.
View SolutionA two digit number is such that the product of its digits, is 8. When 18 is added to the number, they interchange their places. Determine the number.
View SolutionA piece of wire 8m in length is cut into two pieces and each piece is bent into a squares. Where should the cut in the wire be made if the sum of the areas of these squares is to be 2 `m^(2)`?
View SolutionVinay and Praveen working together can paint the exterior of a house in 6 days. vinay by himself can complete the job in 5 days less than Praveen. How long will it take Vinay to complete the job?
View SolutionShow that the sum of roots of a quadratic equation `ax^(2)+bx+c=0 (a ne 0)` is `(-b)/(a)`.
View SolutionShow that the product of the roots of a quadratic equation `ax^(2)+bx+c=0 (a ne 0)` is `(c )/(a)`.
View SolutionThe denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is `2 16/21`, find the fraction.
View SolutionVerify that 1 and `3/2` are the roots of the equation `2x^(2) - 5x + 3 = 0.`
View Solution`If b^(2) - 4ac gt 0 "in" ax^(2) + bx + c = 0,` then what can you say about roots of the equation ? `(a ne 0)`
View SolutionFind the value of k, if 2 is one of the roots of the quadratic equation
`x^(2) - kx + 6 = 0`
View SolutionIn a rectangle ABCD, AB = x + y, BC = x - y, CD = 9 and AD = 3. Find the values of x and y.
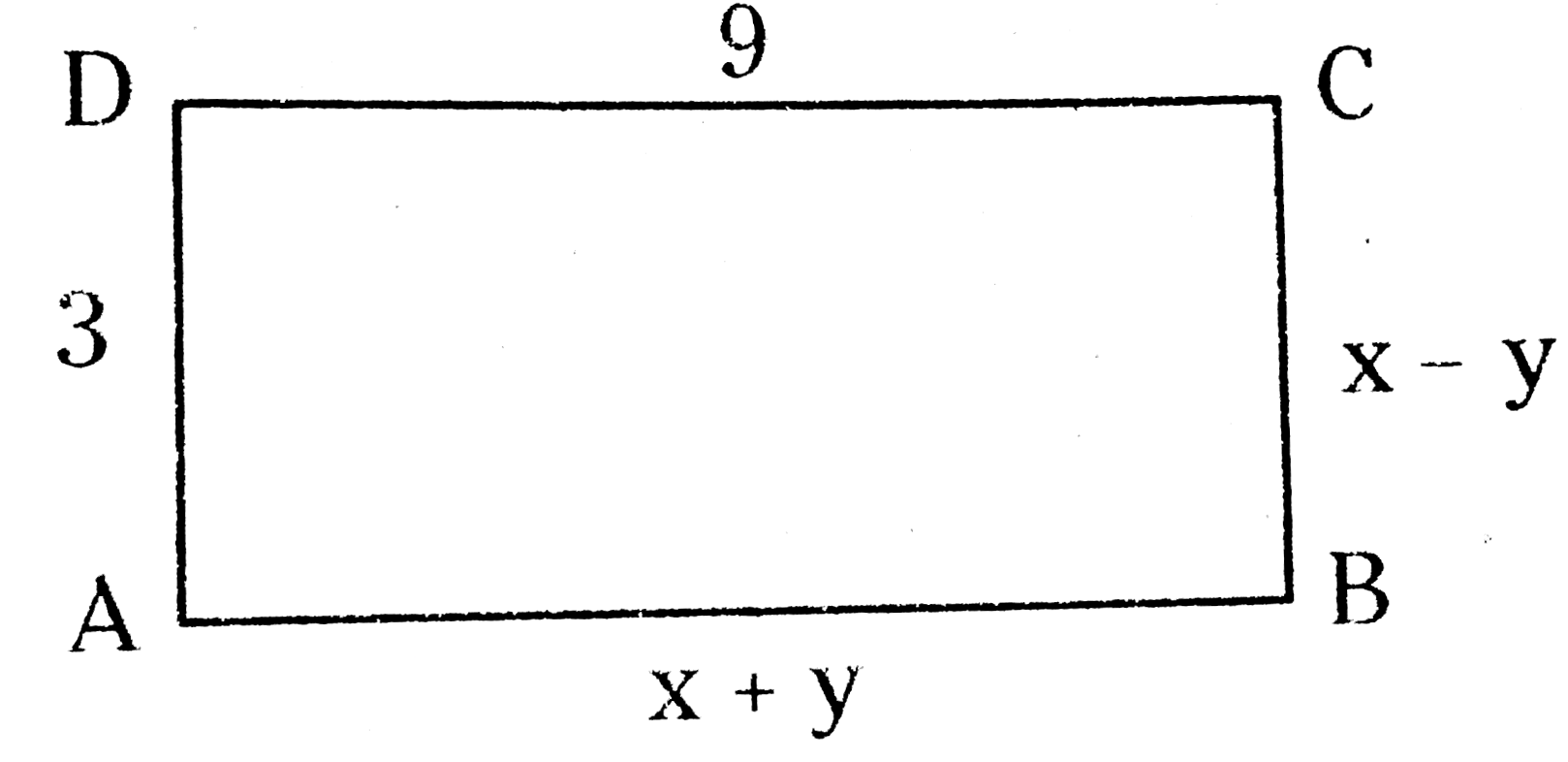
View SolutionWrite the nature of roots of the quadratic equation `2x^(2) - 5x + 6 = 0`
View SolutionWrite the nature of the roots of the quadratic equation`x^(2) - 8x + 16 = 0`
View SolutionFind sum and product of roots of the Quadratic equation
`x^(2) 4 sqrt 3x + 9 = 0`
View SolutionFind the roots of the Quadratic equation `x^2+2x-3=0`.
View Solution
EXERCISE questions and complete solutions for chapter QUADRATIC EQUATIONS of VGS BRILLIANT MATHS (TELUGU ENGLISH) of Class 10