Complete Solutions to ILLUSTRATIVE EXAMPLES of chapter SOME APPLICATIONS OF TRIGONOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | SOME APPLICATIONS OF TRIGONOMETRY |
| ZEN PUBLICATION | ILLUSTRATIVE EXAMPLES |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
A ladder leaning against a wall makes an angle of `60^(@)` with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
View SolutionAn observer 1.7 m tall is `20sqrt(3)` m away from a tower. The angle of elevation from the eye of the observer of the top of the tower is `30^(@)`. Find the height of the tower
View SolutionA flagstaff 7 m long is fixed on the top of a tower standing on the horizontal plane. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 60° and `45^(@)` respectively. Find the height of the tower correct to one decimal place,
View SolutionA bird is sitting on the top of a tree 80 m high. From a point on the ground the angle of elevation of the bird is`45^(@)`. The bird flies horizontally such that it remains at a constant height from the ground. After 2 seconds the angle of elevation of the bird from the same point is `30^(@)`. Find the speed of the flying bird.
View SolutionAs observed from the top of a lighthouse 100 m high abov e sea level, the an g les o f d ep ression o f a ship, sailing directly tow ards it, changes from `30^(@)` to `60^(@)`. Find the distance travelled by the ship during the period of observation.
View SolutionA tower and a pole stand vertically on the same level ground. it is observed that the angles of depression of top and foot of the pole from the top of the tower of height 60m is `30^@` and `60^@` respectively. find the height of the pole.
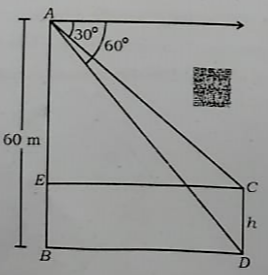
View SolutionA tower and a pole stand vertically on the same level ground. it is observed that the angles of depression of top and foot of the pole from the top of the tower of height 60m is `30^@` and `60^@` respectively. find the height of the pole.

View SolutionFrom the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and p. If the height of the lighthouse is h m etres and the line joining the ships passes through the foot of the lighthouse, show that the distance betw een the ships is
`(h(tan alpha + tan beta))/(tan alpha tan beta)`
View SolutionA vertical tree 15 m high is broken by the wind such that its top just touches the ground and makes an angle of `60^(@)` with the ground. At what height from the ground did the tree break
View SolutionA tower is 50cm high. Its shadow is x mtrs shorter when the suns altitude is `45^(@)` than when it is `30^(@)`. Find the value of x.
View Solution
ILLUSTRATIVE EXAMPLES questions and complete solutions for chapter SOME APPLICATIONS OF TRIGONOMETRY of ZEN MATHS (KANNADA ENGLISH) of Class 10
All Exercises from ZEN PUBLICATION Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY
- ADDITIONAL QUESTIONS ( SHORT ANSWER TYPE-2 QUESTIONS )
- ADDITIONAL QUESTIONS (HOTS (HIGHER ORDER THINKING SKILLS ) QUESTIONS)
- ADDITIONAL QUESTIONS (LONG ANSWER TYPE QUESTIONS )
- ADDITIONAL QUESTIONS (MCQ)
- ADDITIONAL QUESTIONS (SHORT ANSWER TYPE-1 QUESTIONS )
- ADDITIONAL QUESTIONS (VALUE BASED QUESTIONS )
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER TYPE QUESTIONS )
- ILLUSTRATIVE EXAMPLES
- TEXTUAL (EXERCISES 12.1)