Complete Solutions to QUESTION BANK of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| A N EXCEL PUBLICATION | QUESTION BANK |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
If `(x/3+1,y-2/3)=(5/3,1/3)`, find the values
of x and y.
View SolutionIf the set A has 3 elements and the set B = {3,4,5}, then find the number of elements in `(A xx B)`.
View SolutionIf G = {7,8} and H ={5,4,2}, find `Gxx H` and `H xx G`
View SolutionState whether each of the following statetments is true or false. If the statement is false, rewrite the given statement correctly. If P = {m,n} and Q = {n,m}, then `P xx Q` ={(m,n),(n,m)}
View SolutionState whether each of the following statetments is true or false. If the statement is false, rewrite the given statement correctly. If A and B are non -empty sets, then `A xx B` is a non - empty set of ordered pairs (x,y) such that
x `in` A and y `in` B
View SolutionState whether each of the following statetments is true or false. If the statement is false, rewrite the given statement correctly. If A ={1,2}, B = {3,4} then `A xx ( B cap phi) = phi`
View SolutionIf A = { - 1, 1}, find `A xx A xx A`.
View SolutionIf `A xx B`={(a,x), (a,y),(b,x),(b,y)} Find A and B
View SolutionLet `A={1,2}`,`B={1,2,3,4}`,`C={5,6}` and
`D={5,6,7,8}`.Verify that
`Axx(BnnnC)=(AxxB)nnn(AxxC)`
View SolutionLet `A={1,2}`,`B={1,2,3,4}`,`C={5,6}` and
`D={5,6,7,8}`.Verify that
`AxxC` is a subset of `BxxD`
View SolutionLet A = {1,2} and B = {3,4}. Write `A xx B`. How many subsets will `A xx B` have? List them.
View SolutionLet A and B are two sets such that n (A) = 3 and n (B) = 2. If (x,1), (y,2),(z,1) are in `A xx B`, find A and B, where x,y and z are distinct elements.
View SolutionThe Cartesian product `A xx A` has 9 elements among which are found (-1,0) and (0,1). Find the set A and the remaining elements of `A xx A`
View Solution`A={1,2,3,……,14}`. R is a relation from A to A defined by `R={(x,y): 3x-y = 0,x,y in A}`. Write the domain, range,co-domain of ,R.
View SolutionA relation R on set natural numbers is
defined by `R={(x,y):y=x+5`,x is a
natural number less than 4, `x, y in N`}
Write the domain and range of the relation.
View SolutionA = {1,2,3,5} and B = {4,6,9}. Define a relation R from A to B by R = {(x,y): the difference between x and y is odd: ` x in A, y in B}`. Write R in roster from.
View SolutionShows a relationship between the sets P and Q. write this relation in set-builder from

View SolutionShows a relationship between the sets P and Q. write this relation roster from. What is its domain and range ?

View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Write R in roster form.
View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Find the domain of R.
View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Find the range of R.
View SolutionDetermine the domain and range of the
relation R defined by
`R={(x,x+5): x in {0,1,2,3,4,5}}`
View SolutionWrite the relation `R={(x,x^3)`, x is a prime number less than 10}, in roster form.
View SolutionLet A = {x,y,z) and B = {1,2}. Find the number of relations from A to B
View SolutionLet R be the relation on Z defined by R = { ( a,b): a,b `in` Z, a - b is an integer}. Find the domain and range of R
View SolutionWhich of the following relations are functions ? Give reasons. If it is a functions determine its domain and range.{(2,1),(5,1),(8,1),(1,1),(14,1),(17,1)}
View SolutionWhich of the following relations are functions ? Give reasons. If it is a functions determine its domain and range.{(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}
View SolutionWhich of the following relations are functions ? Give reasons. If it is a functions determine its domain and range. {(1,3),(1,5),(2,5)}
View SolutionFind the domain and range of the following functions.
`f(x)=-abs[x]`
View SolutionFind the domain and range of the following functions.
`f(x)=sqrt(9-x^2)`
View SolutionA function f is defined as `f(x)=2x-5`.
Write down the values of `f(0)`,`f(7)`,`f(-3)`.
View SolutionA function f is defined as `f(x)=2x-5`.
Write down the values of `f(0)`,`f(7)`,`f(-3)`.
View SolutionA function f is defined as `f(x)=2x-5`.
Write down the values of `f(0)`,`f(7)`,`f(-3)`.
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t (C ) = (9C)/5 +32`. Find t (0)
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t (C ) = (9C)/5 +32`. Find t (28)
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t (C ) = (9C)/5 +32`. Find t(-10)
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t (C ) = (9C)/5 +32`. Find The value of C, when t (C ) = 212
View SolutionFind the range of the following functions.
`f(x)=2-3x`,`x in R`,`x>0`
View SolutionFind the range of the following functions.
`f(x)=x^2+2`,x is a real number.
View SolutionFind the range of the following functions.
`f(x)=x`,x is a real number.
View SolutionLet R be the set of all real numbers and let `f:R rarr R` be a function defined by `f(x) = x +1` Complete the following table

View SolutionLet R be the set of all real numbers and let `f:R rarr R` be a function defined by `f(x) = x +1` Draw the graph f
View SolutionLet f = {(1,1),(2,8),(3,27),(4,64),} be a function fill in the blanks f(1) = ……, f(2)=……, f(3)=……, f(4)=…….
View SolutionLet f = {(1,1),(2,8),(3,27),(4,64),} be a function write a formula for f (x)
View SolutionGiven the function `f (x) = {-x^2 if xleo`, `5x-4 if 0ltxle1 `, `4x^2-3x if 1ltxlt2`, `3x+4 if xge2` Complete the following table
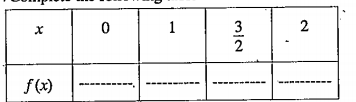
View SolutionIf `(3x, x + y) =( 6,3),` find x and y
View SolutionIf A = {1,2,3}, B = {3,4} and C={4,5,6}, Prove that `A xx (B cap C) =(A xx B) cap (A xx C)`
View SolutionIf A = {1,2,3}, B = {3,4} and C={4,5,6} Prove that `A xx (B cup C) = (A xx B) cup (A xx C)`
View SolutionIf A = {1,2,3}, B = {3,4} and Prove that `A xx B` not= `B xx A`
View SolutionGiven the relations `R_1 = {(x,y) : x,y in N` and `x + y = 6}`
View SolutionGiven the relations `R_2 = {(x,y): x,y in N` and `x^2 + y^2 le 10}`.
View SolutionIf A = {a,b}, write all relation on A
View SolutionFind the domain and range of the relation `R = { (x,y) :y=x^3,x` is a positive prime number` lt 8}`
View SolutionFind the number of relations which can be defined from P = {1,2,3} to Q = {x,y}
View SolutionIf A = {1,2,3} and f is a relation on A defined as follows, then find the given relation is a function or not from A to A ? Explain f = {(1,2),(3,2)}
View SolutionIf A = {1,2,3} and g is relation on A defined as follows, then which of these relations is a function from A to A ? Explain. g = {(1,2),(1,3),(2,3)}
View SolutionIf A = {1,2,3} and h is a relation on A defined as follows, then which of these relations is a function from A to A ? Explain. h = {(1,3),(2,1),(3,2)}
View SolutionLet f : x toY be a function defined by f(x) = `x^2 + 1` for all `x in X` where X = {-1,0,1,2,3} and Y = {1,2,5,10,11}. If A = { -1,0,2} and B = {1,2,3}. Verify that `f (A cap B)= f (A) cap f(B)`
View SolutionLet f : x to Y be a function defined by `f(x) = x^2 + 1` for all `x in X` where X = {-1,0,1,2,3} and Y = {1,2,5,10,11}. If A = { -1,0,2} and B = {1,2,3}. Verify that `f(A cap B) ne f (A) cap f (B)`
View SolutionLet f : x to Y be a function defined by f(x) = `x^2 + 1 for all `x ∈ X` where X = {-1,0,1,2,3} and Y = {1,2,5,10,11}. If A = { -1,0,2} and B = {1,2,3}. verify that f(A-B) =f (A) - f (B)
View SolutionFind the domain and range of the function `f (x) = sqrt( x^2 - 3x +2)`
View SolutionDraw the graph of the function `f(x) = (x^2 - 4)/(x +2)`
View SolutionFind the domain and the range of the functions `f(x) = 1/(2x-1)`
View SolutionFind the domain and the range of the functions `f(x) = x^3`
View SolutionLet `f(x) = x^2 - 2x + 3`. Then find f (f (x) )
View SolutionIf `f (x) =1/(1 - x) `, show that `f(f(f(x))) = x`
View SolutionFind the domain and range of the function `f = {(x, (x^2 -1)/(x - 1)): x in R, x ne 1}`
View SolutionIf `f (x) = x^3 + 1` and `g (x) = x + 1`, find `f + g`,` f - g`, `af (a in R)`,`fg` , `1/f` and `f/g`
View SolutionThe relation f is defined by `f (x) = {(x^2, 0 le x le 3)/(3x, 3 le x le 10)`
The relation g is defined by` g (x) = {(x^2,0 le x le 2)/(3x, 2 le x le 10)`
show that f is a function and g is not a function
View SolutionIf `f(x)=x^2`, find `(f(1.1)-f(1))/((1.1-1))`
View SolutionFind the domain of the following.
`f(x)=(x^2+2x+1)/(x^2-8x+12)`
View SolutionFind the domain and range of the following
functions.
`f(x)=sqrt(x-1)`
View SolutionFind the domain and the range of the real function f defined by `f (x) = abs x - 1`
View SolutionLet `f={(x,x^2/(1+x^2)),x in R}` be a real
function from R to R. Determine the domain
and range of f.
View SolutionLet f,g: R `rarr` R be defined, respectively by `f (x) = x + 1,g (x) = 2x -3`. find `f + g,f - g` and `f/g`
View SolutionLet f = {(1,1), (2,3),(0, -1), (- 1, - 3)} be a function from Z to Z defined by `f (x) = ax + b`, for some integers a,b. determine a,b.
View SolutionLet R be a relation from N to N defined by R = `{(a,b) in N and a = b^2}`. Are the following true? `{(a,a) in R`, for all `a in N`}
View SolutionLet R be a relation from N to N defined by R = `{(a,b) in N and a = b^2}`. Are the following true? `(a,b)in R`, implies `(b,a) in R`
View SolutionLet R be a relation from N to N defined by R = `{(a,b) in N and a = b^2}`. Are the following true? `(a,b) in R, (b,c) in R` implies `(a,c) in R`. Justify your answer .
View SolutionLet `A={1,2,3,4}` `B={1,5,9,11,15,16}` and `f={(1,5),(2,9),(3,1),(4,5),(2,1)}`. State with the reason whether f is a relation or a function.
View SolutionLet A = {1,2,3,4}, B = {1,5,9,11,15,16} and f = {(1,5),(2,9),(3,1),(4,5),(2,11),}. Are the following true? F is a function from A to B. Justify your answer.
View SolutionLet f be the subset of `Z xx Z` defined by `f = {(ab, a + b) : a,b in Z}` is f a function from Z to Z? justify your answer.
View SolutionLet A = {9,10,11,12,13} and let f : A `rarr` N be defined by f (n) = the highest prime factor of n. find the range of f.
View Solution
QUESTION BANK questions and complete solutions for chapter RELATIONS AND FUNCTIONS of A N EXCEL PUBLICATION of Class 11