Complete Solutions to QUESTION BANK of chapter STRAIGHT LINES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | STRAIGHT LINES |
| A N EXCEL PUBLICATION | QUESTION BANK |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Draw a quadrilateral in the cartesian plane whose vertices are `( -4 ,5),(0,7),(5, -5) and (-4, -2)`. also, find its area.
View SolutionThe base of an equilateral triangle with side 2a lies along the `y` - axis such that the midpoint of the base is at the origin. Find vertices of the triangle.
View SolutionFind the distance between `P (x_1,y_1)` and `Q (x_2,y_2)` when PQ is parallel to the y-axis.
View SolutionFind the distance between `P (x_1,y_1)` and `Q (x_2,y_2)` when PQ is parallel to the X-axis.
View SolutionFind a point on the x-axis,which is equidistant from the points (7,6) and (3,4)
View SolutionFind the slope of a line, which passes through the orgin and the mid point of the line segment joining the points P(0,-4) and B (8,0)
View SolutionWithout using the pythagoras theorem show that the points (4,4),(3,5) and (-1, -1) are the vertices of a right angled triangle.
View SolutionFind the slope of the line, which makes' angle of `30^(circ)` with the positive direction of y- axis measured anticlockwise.
View SolutionFind the value of x for which the points (x,-1),(2,1)and(4,5) are collinear.
View SolutionWithout using distance formula, show that (-2, -1),(4,0),(3, 3) and (-3,2) are the vertices of a parallelogram.
View SolutionFind the angle between the positive x-axis and the line joining the points (3,-1) and (4,-2).
View SolutionThe slope of a line is double of the slope of another line. if tangent of the angle between them is `1/3` find the slopes of the lines.
View SolutionA line passes through `(x_1,y_1)` and (h,k). if the slope of the line is m, show that `k - y_1 = m(h-x_1)`
View SolutionIf three points (h,0), (a,b) and (0,k) lie on a line, show that `a/h + b/k =1`
View SolutionConsider the following population and year hraph (sec figure). find the slope of the line AB and using it, find what will be the population in the year 2010?
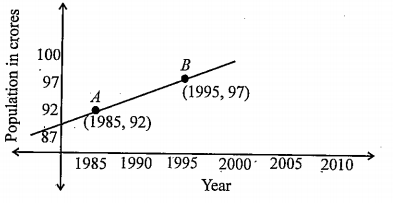
View SolutionFind the slope of the line joining (x,- 1) and (2,1)
View SolutionFind the slope of the line joining (2,1) and (4,5)
View SolutionFind the value of x for which the points (x,-1),(2,1)and(4,5) are collinear.
View SolutionConsider the line passing through the points (3,4) and (x,5) Find the slope of the line
View SolutionConsider the line passing through the points (3,4) and (x,5) if the line makes an angle of `135^@` with positive direction of x-axis, find the value of x.
View SolutionFind the slope of the line through (3,y) and (2,7)
View SolutionFind the slope of the line passing through (-1,4) and (0,6)
View SolutionIf the lines passing through (3,y) and (2,7) are parallel to the line through (– 1, 4) and (0, 6) find the value of y
View SolutionIf the lines passing through (3,y) and (2,7) are perpendicular find the value of y
View SolutionConsider the triangle with vertices A (4,4),B (3,5) and C (-1,-1) Using pythagoras theorem prove that `Delta` ABC is right angled.
View SolutionWithout using the pythagoras theorem show that the points (4,4),(3,5) and (-1, -1) are the vertices of a right angled triangle.
View SolutionConsider a quadrilateral whose vertices are A (- 4,2),B (2,6), C (8,5) and D (9,7) Find the mid point of the sides of the quadrilateral.
View SolutionConsider a quadrilateral whose vertices are A (- 4,2),B (2,6), C (8,5) and D (9,7) Find the mid point of the sides of the quadrilateral.
View SolutionFind the equation of a line that has y-intercept 5 and is perpendicular to the line joining (2, -3) and (4,2)
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points A (2,3) and B (6, -5).
View SolutionIn what ratio is the line joining the points (4, -5) and (2,3) divided by the line passing through the points (6,8) and (-3,-2).
View SolutionFind the equation to the straight line which passes through the point (5,6) and has intercepts on the axes equal in magnitude and both positive.
View SolutionThe `bot r` distance of a line from the origin is 5 cms and its slope is `-1`. find the equation of the line
View SolutionWrite the equation for x- axis and y-axis.
View SolutionFind the equation of the line passing through (-4,3) and with slope `1/2`
View SolutionFind the equation of the line passing through (0,0) with slope m.
View SolutionFind the equation of the line passing through `(2,2 sqrt 3)` and inclined with the x-axis at an angle of `75^@`
View SolutionFind the equation of the line intersecting the x-axis at a distance of 3 units to the left of origin with slope -2.
View SolutionFind the equation of the line intersecting the y-axis at a distance of 2 units above the origin and making an angle of `30^@` with the positive direction of the x-axis.
View SolutionFind the equation of the line passing through (-1,1) and (2, -4)
View SolutionFind the equation the following lines satisfying the given conditions.
perpendicular distance from origin is 5 units and the angle the perpendicular makes with the positive direction of x-axis is `30°`.
View SolutionThe vertices of `Delta` PQR are P (2, 1),Q (-2,3) and R (4,5).find the equation of the median through the vertex R.
View SolutionFind the equation of the line passing through the point (-3,5) and perpendicular to the line through the points (2,5) and (-3,6).
View SolutionA line perpendicular to the line segment joining the points (1,0) and (2,3) divides it in the ratio 1:n. find the equation of the line.
View SolutionFind the equation of the line that cut off
equal intercepts on the coordinate axis and
passes through the point (2,3)
View SolutionFind the equation of the line passing through the point (2,2) and cutting off intercepts on the axis whose sum is 9.
View SolutionFind the equation of the line through the point (0,2) making an angle `(2pi)/3` with the positive x-axis,also find the equation of the line parallel to it and crossing the y-axis at a distance 2 units below the origin.
View SolutionThe perpendicular from the origin to a line meets it at the point (-2,9),find the equation
of the line.
View SolutionThe length L (in cms) of a copper rod is a linear function of its celsius temperature C. in an experiment, if L = 124.942 when C = 20 and L =125.134 when C = 110 express L interms of C.
View SolutionThe owner of a milk store finds that he can sell 980 litres of milk each week at Rs. 14/litre and 1220 litres of milk each week at Rs. 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs.17/litre.
View SolutionP(a,b) is the mid-point of a line segment between axis. Show that equation of the line is `x/a+y/b=2`
View SolutionPoint R (h,k) divides the line segment between the axes in the ratio 1:2. find the equation of the line.
View SolutionBy using the concept of equation of a line, prove that the three points (3,0),(-2,-2) and (8,2) are collinear.
View SolutionLook at the following figures. By observing the figures write down their cartesian equations
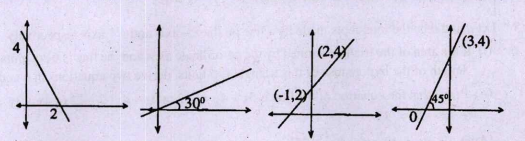
View SolutionWhat is the geometric property possessed by the straight lines of each system given by `y = mx + 8`
View SolutionWhat is the geometric property possessed by the straight lines of each system given by `y = 6x + 8`
View SolutionWhat is the geometric property possessed by the straight lines of each system given by `9x + 6y = k`
View SolutionWhat is the geometric property possessed by the straight lines of each system given by `y +4 = m (x - 5)`
View SolutionWhat is the geometric property possessed by the straight lines of each system given by `1 = x/a + y/3`
View SolutionWhat is the geometric property possessed by the straight lines of each system given by `(4x + 3y + 2) + k (3x + 7y) = 0`
View SolutionFind the slope of the line joining the points `(a cos theta , b sin theta)` and `(a cos phi, b sin phi)`
View SolutionIf the line joining the points `(a cos theta , b sin theta)` and `(a cos phi, b sin phi)`.Prove that the equation of this lines is `x/a "cos" (theta + phi)/2 + y/b"sin" (theta + phi)/2 = "cos" (theta -phi)/2`
View SolutionFind the equation of the line joining the points (2,3) and (4,1)
View SolutionFind the co-ordinates of the point which divides the line joining the points (-3,4) and (-1,-2) in the ratio l : m
View SolutionFind the ratio of division in the point of division lies on the line in
View SolutionConsider the points A (2,3) and B (6,5) Find the co-ordinates of the mid point of the segment joining A and B
View SolutionConsider the points A (2,3) and B (6,5) find the slope of AB
View SolutionConsider the points A (2,3) and B (6,5) What is the slope of a line perpendicular to AB?
View SolutionConsider the points A (2,3) and B (6,5) Find the equation of the perpendicular bisector of the line segment AB
View SolutionLet a and b be the intercepts made by a line on the x-axes and y-axes respectively If the area of the triangle formed by the co-ordinate axes and the line is 6 sq. units and the lenght of the hypotenuse of this triangle is 5 units, derive two equations in a and b
View SolutionLet a and b be the intercepts made by a line on the x-axes and y-axes respectively.If the area of the triangle formed by the coordinate axis and the line is 6 square units and length of the hypotenuse is 5 units. Prove that the equation of the line is 3x + 4y = 12 or 3x + 4y = -12 or 4x + 3y = 12 or - 4x - 3y = 12
View SolutionSuppose that two opposite vertices of a square are (1,2) and (5,8) Find the co-ordinates of its other two vertices
View SolutionSuppose that two opposite vertices of a square are (1,2) and (5,8) Find the equations of the sides of the square
View SolutionConsider the points P (2,4) and Q (-2,5) Find the slope of PQ
View SolutionConsider the points P (2,4) and Q (-2,5) Find the mid point of PQ Hence, find the equation of the perpendicular bisector of PQ
View SolutionSuppose D (2,1), E (-5,7),F(-5,-5) are the mid points of the sides AB,BC and CA of the triangle ABC Find the slope of DF,DE and EF
View SolutionSuppose D (2,1), E(-5,7),F (-5,-5) are the mid points of the sides AB,BC and CA of the triangle ABC Find the equation of the sides AB, BC and CA
View SolutionReduce the equation `sqrt 3 x + y + 2 `= 0 to : slope - intercept from and find slope and y - intercept ,
View SolutionReduce the equation `sqrt 3 x + y + 2 = 0 `to : intercept form and find intercepts on the axes:
View SolutionReduce the equation `sqrt 3 x + y + 2 = 0 `to : the normal from and find p and `alpha`
View SolutionIf p be the measure of the perpendicular segment from the origin on the line whose intercepts on the axis are a and b show that `1/p^2= 1/a^2 + 1/b^2`
View SolutionFind the distance of the point (- 2,3) from the line x - y = 5.
View SolutionFind the distance of the point (4,2) from the line joining (4,1) and (2,3).
View SolutionReduce the following equations into slope intercept form and find their slopes and the y-intercepts.
i) `x+7 y=0`
ii) `6 x+3 y-5=0`
(iii) `y=0`
View SolutionReduce the equation `6x+3y-5=0` into slope intercept form and hence find it slope and y-intercept
View SolutionReduce the following equation into slope intercept form and find their slopes and the y-intercepts `x+7y = 0`
View SolutionFind the x and y intercepts of the line `3x+4y-12=0`
View SolutionFind the slope,x-intercept and y-intercept of the following lines.
`4x-3y=6`
View SolutionReduce the following equation into slope intercept from and find their intercepts on the axes. `3y + 2 = 0`
View SolutionReduce of the following equation into normal from. Find their perpendicular distance from the origin and angle between perpendicular and the positive x-axis.`x- sqrt 3y + 8 = 0`
View SolutionReduce the following equation into normal from. Find their perpendicular distance from the origin and angle between perpendicular and the positive x-axis.`y - 2 = 0`
View SolutionReduce the following equation into normal form. Find their perpendicular distance from the origin and angle between perpendicular and the positive x-axis.`x - y = 4`
View SolutionFind the distance of the point (-1,1) from the line 12(x + 6) = 5 (y - 2)
View SolutionFind the points on the x-axis, whose distance from the line `x/3 + y/4 ` = 1 are 4 units.
View SolutionFind the distance between the parallel lines 15x + 8y - 34 = 0 and 15x + 8y + 31 = 0
View SolutionFind the distance between the parallel lines l (x + y) +p = 0 and l (x + y) - r = 0
View SolutionFind the equation of the line parallel to the line `3x-4y+2=0` and passing through
the point (-2,3).
View SolutionFind the equation of the line perpendicular
to the line `x-7y+5=0` and having x-intercept 3.
View SolutionFind angles between the lines `sqrt 3 x + y = 1` and `x + sqrt 3 y = 1`
View SolutionThe line through the points (h,3) and (4,1) intersects the line 7x - 9y - 19 = 0 at right angle. find the value of h.
View Solution
QUESTION BANK questions and complete solutions for chapter STRAIGHT LINES of A N EXCEL PUBLICATION of Class 11