Complete Solutions to Chapter Test of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| A2Z | Chapter Test |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
The magnitude of vector `vec(A),vec(B)` and `vec(C )` are respectively 12,5 and 13 unit and `vec(A)+vec(B)= vec(C )` then the angle between `vec(A)` and `vec(B)` is
View SolutionThe angle between the two vector `vec(A)= 5hat(i)+5hat(j)` and `vec(B)= 5hat(i)-5hat(j)` will be
View SolutionAngle between the vectors `(hat(i)+hat(j))`and `(hat(j)-hat(k))` is
View SolutionIf the resultant of `n` forces of different magnitudes acting at a point is zero, then the minimum value of `n` is
View SolutionFind the resultant of the three vectors `vec(OA), vec(OB)` and `vec(OC)` shown in figure. Radius of the circle is R.

View SolutionA person goes `10 km` north and `20 km` east. What will be displacement from initial point ?
View SolutionLet `vec(C )= vec(A)+vec(B)` then
View SolutionIn figure, `vec(E )` equals
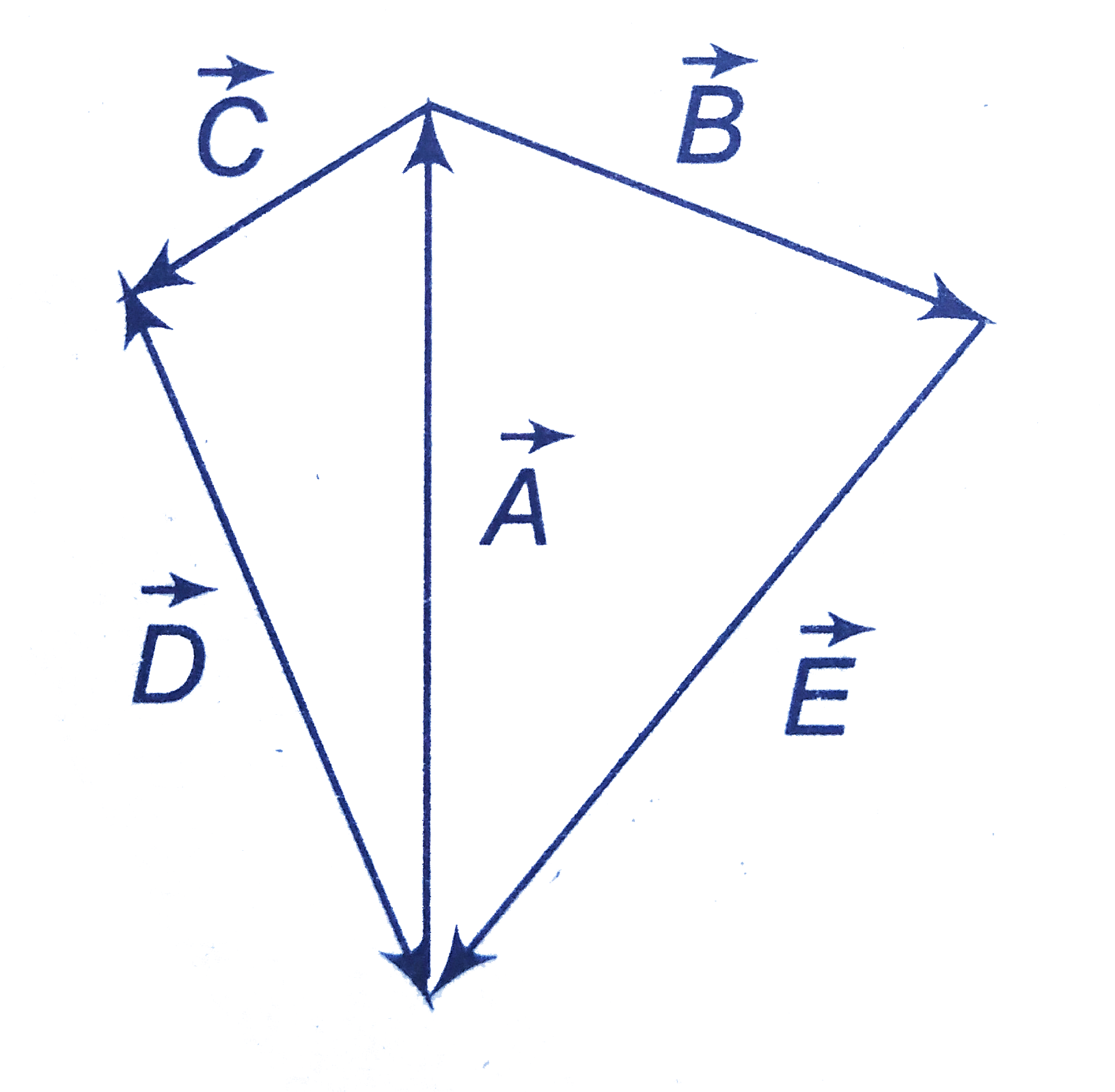
View SolutionA scooter going due east at `10 ms^(-1)` turns right through an angle of `90^(@)`. If the speed of the scooter remain unchanged in taking turn, the change is the velocity the scooter is
View SolutionGiven that `vec(A)+vec(B)=vec(C )` and that `vec(C )` is perpendicular to `vec(A)` Further if `|vec(A)|=|vec(C )|`, then what is the angle between `vec(A)` and `vec(B)`
View SolutionThe component of a vector `r` along X-axis will have maximum value if
View SolutionA particle moves so that its position vector varies with time as `vec(r )= A cos omegathat(i)+A sin omega t hai(j)`. The initial velocity of the particel the particle is
View Solution`hat(e )_(r)` is unit Vector along radius of a circle shown in figure `hat(e )_(r)` can be represented as `
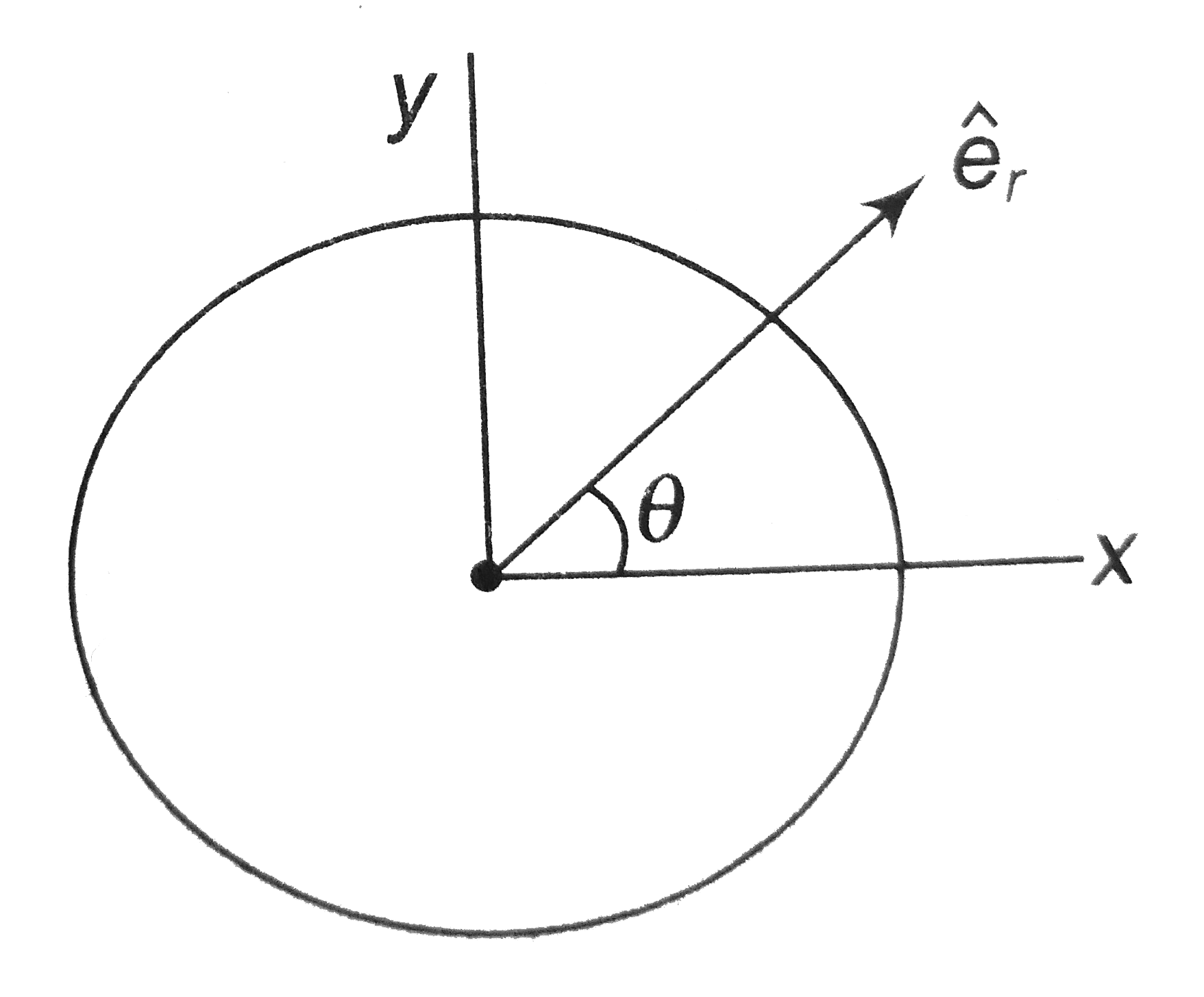
View SolutionA vector of magnitude `10 N` acting in X-Y-plane has componets `8 N` and `6 N` along positive X-axis and positive Y-axis, repectively.The coordinate system is rotated about Z-axis through angle `90^(@)` in anti-clockwise direction. Find x-components and y-component in new coordinate system.
View SolutionA particle P is acted by three coplanar forces as shown in the figure

Find the force needed to prevent the particle P from moving.(taking, sqrt(3)=1.7)`
View SolutionA person moves `30 m` north, then `30 m`, then `20 m` towards east and finally `30sqrt(2) m` in south-west direction. The displacement of the person from the origin will be
View SolutionA particle moves from position `3hat(i)+2hat(j)-6hat(k)` to `14hat(i)+13hat(j)+9hat(k)` due to a uniform force of `4hat(i)+hat(j)+3hat(k)N`. If the displacement is in meters, then find the work done by the force.
View SolutionNormal reaction `N` is a force exerted by the surface on the block perpendicular to the surface to contact. A block of mass `1 kg` is placed on inclined plane of inclintation `37^(@)` as shown in the figure
Find the component of normal reaction `N= 8 N` on the block x-axis and y-axis
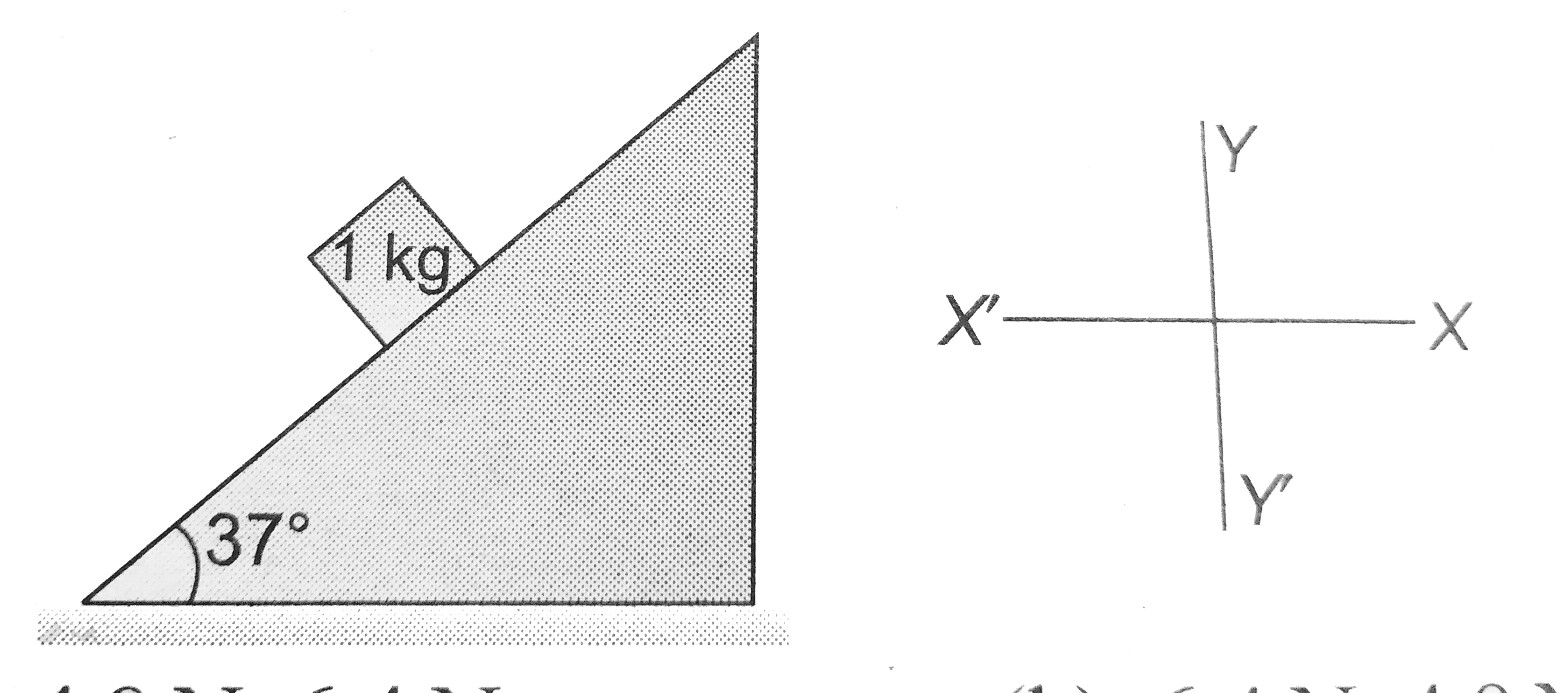
View SolutionWeight mg of a block is a force acting downward toward centre of the earth. A block of mass `1 kg` is placed on an inclined plane as shown in figure. Find the x-component and y-component of weight of the block are

View SolutionThree forces are acting on a particle as shown in the figure. To have the resultant force only along the Y-direction, the magnitude of the maximum additional force needed is
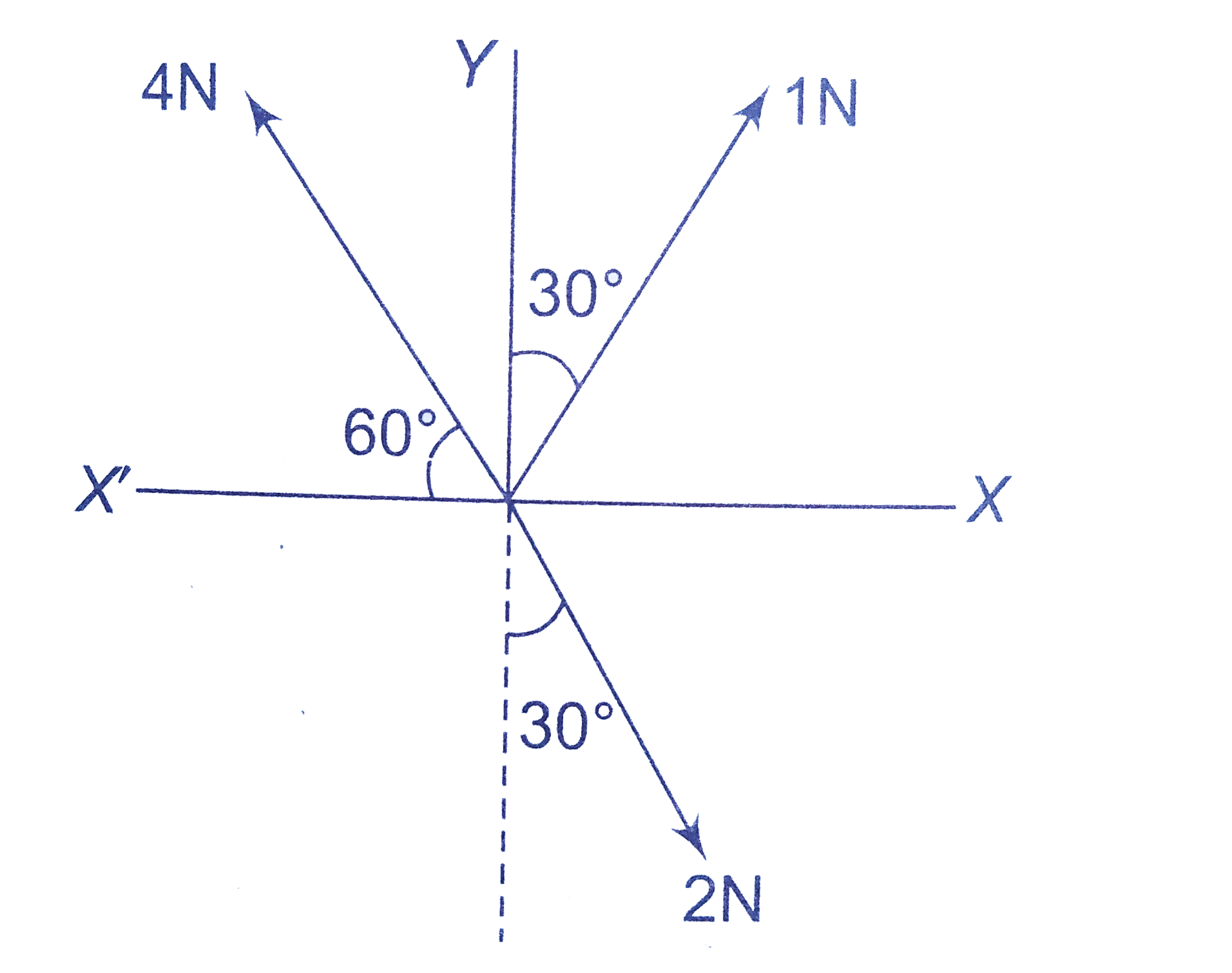
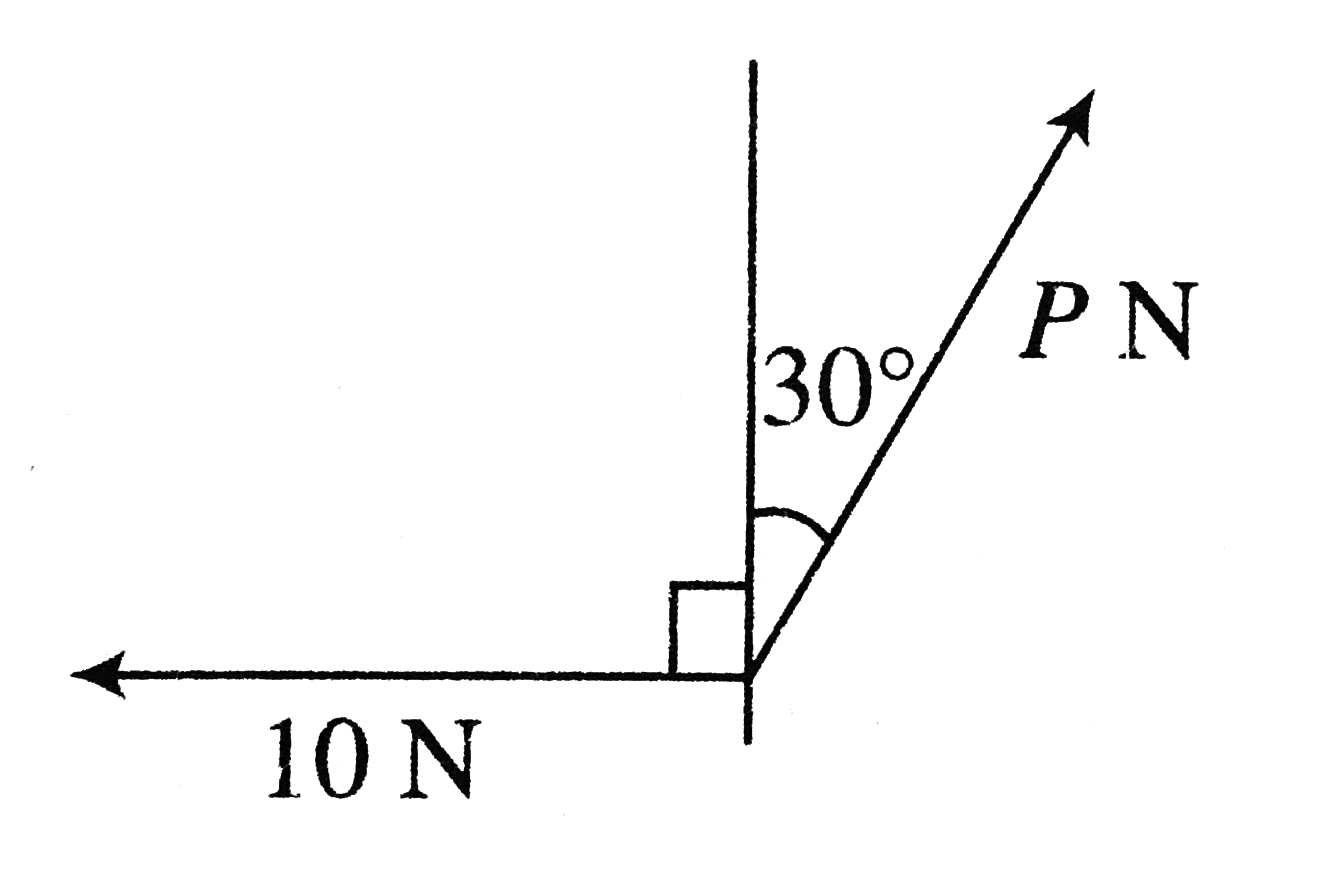
View SolutionTwo horizontal forces of magnitudes of `10N` and `P N` act on a particle. The force of magnitude `10N` acts due west and the force of magnitude `P N` acts on a bearing of `30^(@)` east of north as shown in figure. The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionP, Q and R are three coplanar forces acting at a point and are in equilibrium. Given `P= 1.9318 kg-wt, sin theta_(1)= 0.9659`, the value of R is `(in kg-wt)`
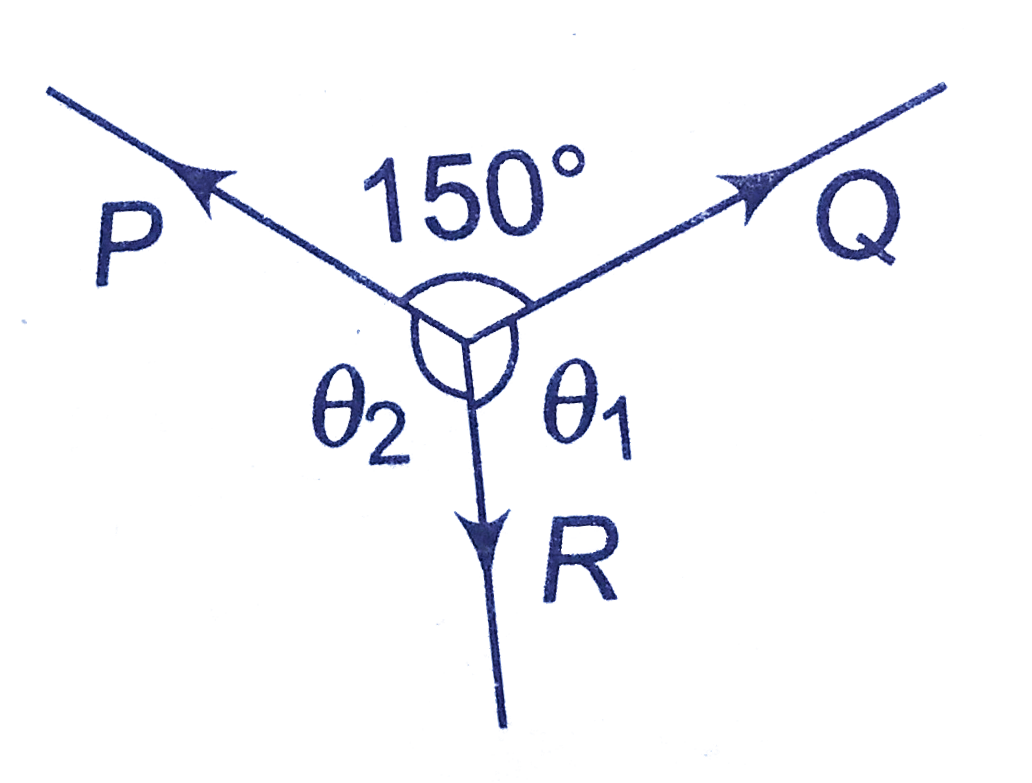
View SolutionFive forces `2 N, sqrt(3)N, 5 N, sqrt(3) and 2 N` respectively act at a particel `P` as shown in figure.
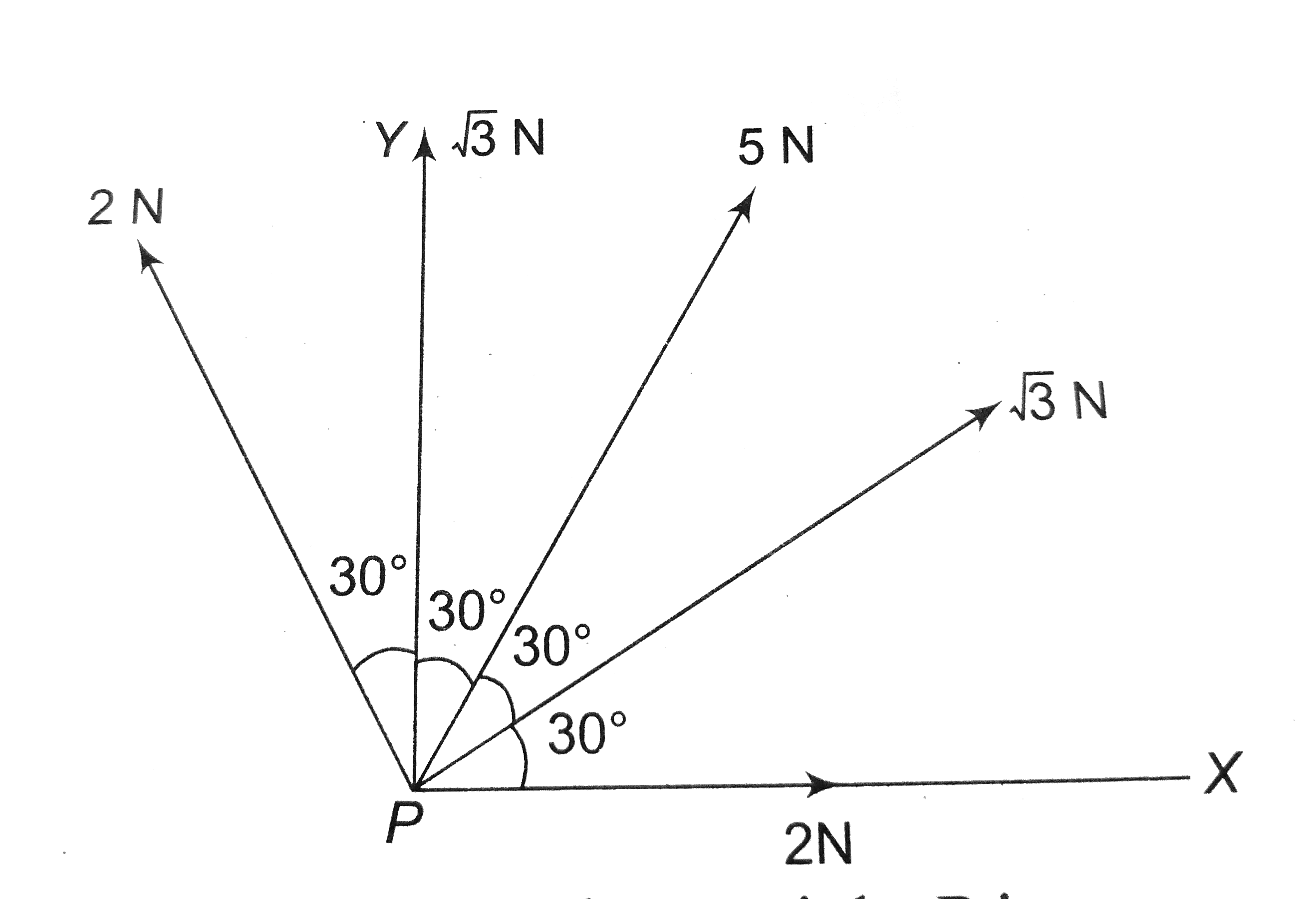
The resultant force on the particle `P` is
View SolutionConsider two Vectors `vec(F)_(1)= 2hat(i)+5hat(k)` and `vec(F)_(2)= 3hat(j)+4hat(k)`. The magnitude of the scalar product of these Vector is
View SolutionA particle moves with a velocity `6hat(i)-4hat(j)+3hat(k)m//s` under the influence of a constant force `vec(F)= 20hat(i)+15hat(j)-5hat(k)N`.
The instantaneous power applied to the particle is
View SolutionThe length of second's hand in watch is `1 cm`. The change in Velocity of its tip in 15 seconds is
View SolutionAsserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.
View SolutionAssertion: Multiplying any vector by an scalar is meaningful operatons.
Reason: In uniform motion spedd remains constant.
View SolutionAssertion: If `hat(i)` and `hat(j)` are unit Vectors along x-axis and y-axis respectively, the magnitude of Vector `hat(i)+hat(j)` will be `sqrt(2)`
Reason: Unit vectors are used to indicate a direction only.
View Solution
Chapter Test questions and complete solutions for chapter VECTORS of A2Z PHYSICS (HINGLISH) of Class 11