Complete Solutions to Problems Based On Basic Concept Of Projectile Motion of chapter MOTION IN TWO DIMENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN TWO DIMENSION |
| A2Z | Problems Based On Basic Concept Of Projectile Motion |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
Which of the following quantities remain constant during projectile motion?
02:31View SolutionIn case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?
01:17View SolutionIf air resistance is not considered in projectiles, the horizontal motion takes place with:
01:15View SolutionWhen a projectile is fired at an angle `theta` w.r.t horizontal with velocity u, then its vertical component:
02:25View SolutionTwo bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit the ground first?
02:17View SolutionIn a projectile motion the velocity
02:47View SolutionWhich out of these does not affect the maximum height of a projectile?
00:47View SolutionThree particles A, B and C are projected from the same point with the same initial speeds making angles `30^(@), 45^(@) and 60^(@)` respectively with the horizontal. Which of the following statement is correct?
02:31View SolutionA particle reaches its highest point when it has covered exactly one half of its horizontal range. The corresponding point on the displacement -time graph is charecterized by :
04:25View SolutionWhen air resistance is taken into account while dealing with the motion of the projectile which of the following properties of the projectile, shows an increases?
05:39View SolutionWhich of the following sets of factors will affect the horizontal distance covered by an converted by an athlete in a long- jump event?
02:08View SolutionA particle projected with velocity u at angle `theta` with horizontal at t=0. What is the magnitude of change in the velocity of the particle when it is at maximum height?
03:13View SolutionTwo projectiles are fired from the same point with the same speed at angles of projection `60^(@) and 30^(@)` respectively. Which one of the following is true?
07:41View SolutionFor angles of projection of a projectile at angle `(45^(@) - theta) and (45^(@)+ theta)`, the horizontal ranges described by the projectile are in the ratio of :
02:16View SolutionFour bodies A,B,C and D are projected with equal velocities having angles of projection `15^(@),30^(@),45^(@) and 60^(@)` with the horizontal respectively. The body having the shortest range is
02:06View SolutionTwo stones are projected with the same speed but making different angles with the horizontal. Their ranges are equal. If the angles of projection of one is `pi//3` and its maximum height is `h_(1)` then the maximum height of the other will be:
03:02View SolutionA gun is firing bullets with velocity `v_0` by rotating it through `360^@` in the horizontal plane. The maximum area covered by the bullets is
04:47View SolutionA particle is projected with a velocity u making an angle `theta` with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
03:11View SolutionThe range of a projectile launched at an angle of `15^(@)` with horizontal is `1.5km`. The range of projectile when launched at an angle of `45^(@)` to the horizontal is
02:30View SolutionA gun fires two bullets at `60^(@) and 30^(@)` with the horizontal. The bullets strike at some horizontal distance. The ratio of maximum height for the two bullet is
02:44View SolutionA shell fired from the ground is just able to cross in a horizontal direction the top of a wall 90m away and 45m high. The direction of projection of the shell will be:
03:04View SolutionIn the previous problem, the velocity of the shell will be
03:59View SolutionIf R is the maximum horizontal range of a particle, then the greatest height attained by it is :
02:51View SolutionA particle is projected with a velocity v, so that its range on a horizontal plane is twice the greatest height attained. If g is acceleration due to gravity, then its range is :
06:17View SolutionDuring a projectile motion if the maximum height equal the horizontal range, then the angle of projection with the horizontal is :
01:26View SolutionThe point from where a ball is projected is taken as the origin of the coordinate axes. The x and y components of its displacement are given by `x=6t and y=7t-5t^(2)`. What is the velocity of projection?
02:21View SolutionIn the previous problem, What is the angle of projection ?
02:37View SolutionA body is projected at an angle of `30^(@)` with the horizontal and with a speed of `30ms^(-1)`. What is the angle with the horizontal after 1.5 second? `(g=10ms^(-2))`
03:44View SolutionA body of mass `2 kg` has an initial velocity of `3 m s^-1` along `OE` and it is subjected to a force of `4 N` in `O F` direction perpendicular to `O E`. Find the distance of the body from `O` after `4 s`.
 .03:39View Solution
.03:39View SolutionA body has an initial velocity of `3m//s` and has an acceleration of `1m//sec^(2)` normal to the direction of the initial velocity. Then its velocity 4 seconds after the start is
03:29View SolutionA person can throw a stone to a maximum distance of `h` meter. The greatest height to which he can throw the stone is:
02:28View SolutionA person can throw a stone to a maximum height of h meter. The maximum distance to which he can throw the stone is:
02:07View SolutionA projectile can have the same range 'R' for two angles of projection . If `'T_(1)'` and `'T_(2)'` to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .
03:16View SolutionThe equation of motion of a projectile is `y = 12 x - (3)/(4) x^2`. The horizontal component of velocity is `3 ms^-1`. What is the range of the projectile ?
03:01View SolutionThe trajectory of a projectile in a vertical plane is `y=ax-bx^(2)`, where a and b are constants and x and y are respectively horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projection form the horizontal are:
04:48View SolutionA projectile is given an initial velocity of ` ( hat(i) + 2 hat (j) ) m//s`, where ` hat(i)` is along the ground and `hat (j)` is along the vertical . If ` g = 10 m//s^(2) `, the equation of its trajectory is :
02:30View SolutionTwo particles are projected obliquely from ground with same speed such that their range `'R'` are same but they attain different maximum heights `h_(1)` and `h_(2)` then relation between `R, h_(1)` and `h_(2)` is:
03:51View SolutionA stone is thrown at an angle `theta` to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
04:04View SolutionA cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
02:43View SolutionThe speed of a projectile at its maximum height is `sqrt3//2` times its initial speed. If the range of the projectile is n times the maximum height attained by it, n is equal to :
03:46View SolutionA body is projected at an angle of `60^(@)` with ground. It covers a horizontal distance of 100m. If the same body is projected at `60^(@)` with vertical with same velocity, the new range is
03:09View SolutionTwo paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: `(g=10ms^(-2))`
04:22View SolutionThe ceiling of a hall is 40m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of `56ms^(-1)` without the ceiling of the hall is
View SolutionIn the previous problem, the maximum horizontal distance will be
02:44View SolutionTwo bodies are thrown with the same initial velocity at angles ` theta ` and `(90^@ - theta)` respectively with the horizontal, then their maximum height are in the ratio
01:05View SolutionIf R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
02:07View SolutionIf a ston s to at a point which is at a distance d away and at a height h avove the point from where the stone starts, then what is the value of initial speed u if the stone is lauched at angle `theta`?
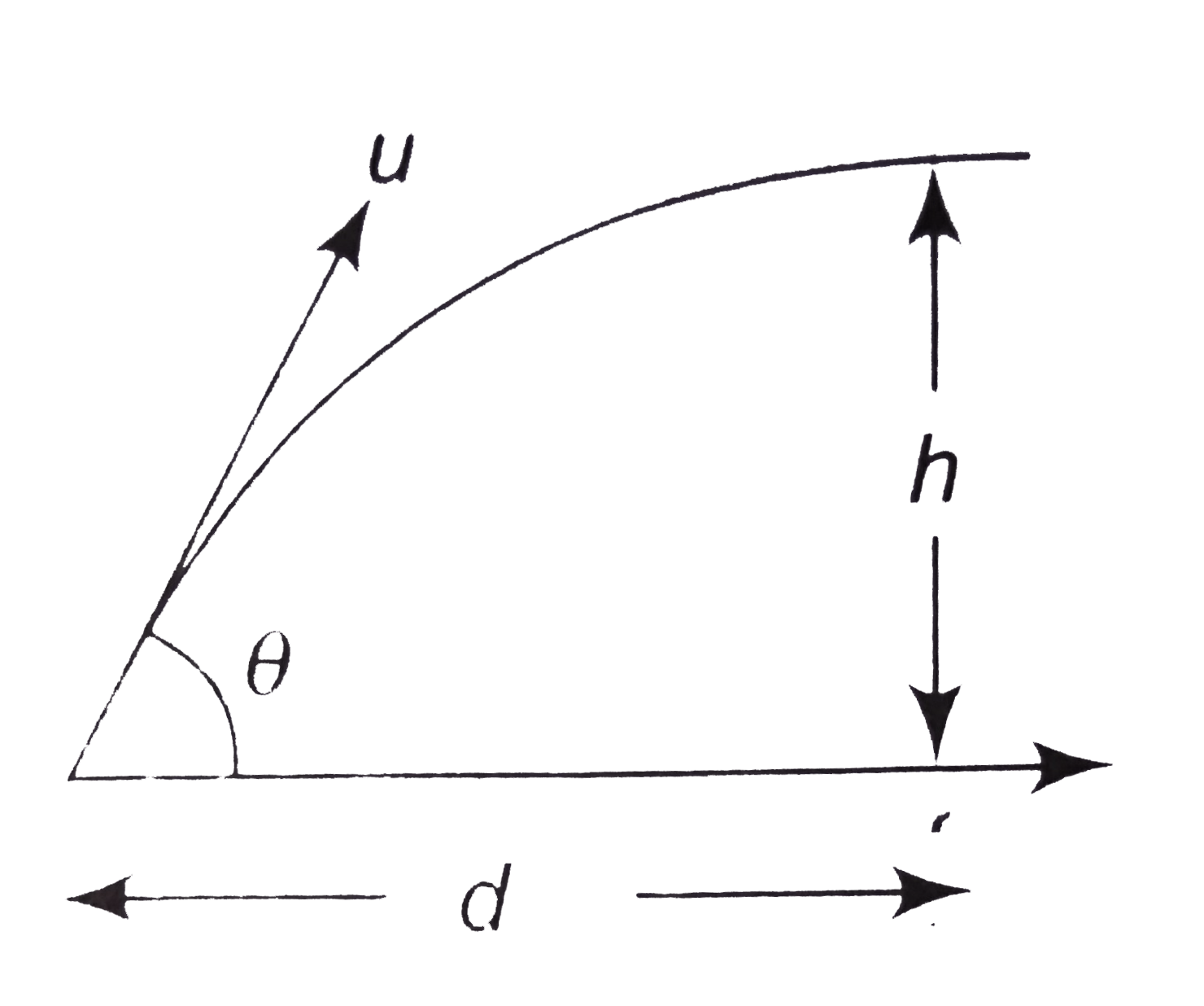 06:25View Solution
06:25View SolutionA particle is projected from the ground with an initial speed of v at an angle `theta` with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
06:27View SolutionTwo particls are projected in air with speed u at angles `theta_(1) and theta_(2)` (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then which one of the following is correct? where `T_(1) and T_(2)` are the time of flight.
03:37View Solution
Problems Based On Basic Concept Of Projectile Motion questions and complete solutions for chapter MOTION IN TWO DIMENSION of A2Z PHYSICS (HINGLISH) of Class 11
