Complete Solutions to Kinetic Theory Of Gases of chapter KINETIC THEORY OF GASES AND THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES AND THERMODYNAMICS |
| A2Z | Kinetic Theory Of Gases |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
Four molecules of a gas are having speeds of `1, 4, 8` and `16 ms^(-1)`. The root mean square velocity of the gas molecules is
View SolutionAn ideal gas is heated at constant volume until its pressure doubles. Which one of the following statements is correct?
View SolutionIf the volume of a gas is doubled at constant pressure, the average translational kinetic energy of its molecules will
View SolutionThe average translational kinetic energy of the molecules of a gas will be doubled if at constant
View SolutionThe ratio of the number of moles of a monoatomic to a polyatomic gas in a mixture of the two, behaving as an diatomic gas is : (vibrational modes of freedom is to be ignored)
View SolutionIf masses of all molecules of a gas are halved and the speed doubled. Then the ratio of initial and final pressure is :
View SolutionThe average kinetic energy of `H_(2)` molecules at `300 K` is `E` at the same temperature the average kinetic energy of `O_(2)` molecules is :
View SolutionMolecular hydrogen at one atmosphere and helium at two atmosphere occupy volume `V` each at the same temperature. The rms velocity of hydrogen molecules is `x` times the rms velocity of helium molecules. What is the value of `x`?
View SolutionWhat is the ratio of the total energy of all the molecules of one mole of `O_(2)` to the total energy of all the molecules of two moles of helium at the same temperature?
View SolutionOn the basis of kinetic theory of gases, the mean `K.E.` of `1 mole per degree` of freedom is
View SolutionAt a certain temperature, the rms velocity for `O_(2)` is `400 ms^(-1)`. At the same temperature, the rms velocity for `H_(2)` molecules will be
View SolutionA gas in a vessel is at the pressure `P_(0)`. If the masses of all the molecules be made half and their speeds be made double, then find the resultant pressure.
View SolutionThe energy density `u/V` of an ideal gas is related to its pressure P as
View SolutionThe molecular weighs of oxygen and hydrogen are 32 and 2 respectively. The root mean square velocities of oxygen and hydrogen at `NTP` are in the ratio
View SolutionA sample of oxygen is compressed to half of its original volume at constant temperature. If the rms velocity of gas molecules was originally C, their new rms velocity is
View SolutionAt what temperature is the `K.E`. Of a gas molecules half that of its value at `27^(@)C`
View SolutionOxygen and hydrogen in two enclosures have same mass, volume and pressure. The ratio of the temperatures of the two gases is
View Solution`250 litre` of an ideal gas is heated at constant pressure from `27^(@)C` such that its volume becomes `500 litre`. The final temperature is
View SolutionThe rms velocity of hydrogen gas molecules at `NTP` is `V rms^(-1)`. The gas is heated at constant volume till the pressure becomes four times. The final rms velocity is
View SolutionThe rms speed of oxygen molecules at a certain temperature `T` is `v`. If the temperature is doubled and oxygen gas dissociates into atomic oxygen, then the rms speed
View SolutionThe ratio of the vapour densities of two gases at the same temperature is `8:9`. The ratio of the rms velocities of their molecules is
View SolutionTwo perfect gases at absolute temperature `T_(1) and T_(2)` are mixed. There is no loss of energy. The masses of the molecules are `m_(1) and m_(2)`. The number of molecules in the gases are `n_(1) and n_(2)`. The temperature of the mixture is
View SolutionAt what temperature, rms velocity of `O_(2)` molecules will be `1//3` of `H_(2)` molecules at `-3^(@)C`
View SolutionWhen the temperature of a gas is raised from `27^(@)C` to `90^(@)C`, the percentage increase in the rms velocity of the molecules will be
View SolutionAn assembly of smoke particle in air at `NTP` is under consideration. If the mass of each particles is `5 xx 10^(-17) kg`. Then the rms speed is
(Given: `k = 1.38 xx 19^(-23) J K^(-1)`)
View SolutionFour molecules of a gas have speed `1, 2, 3 and 4 km s^(-1)` respectively. The value of rms speed of the molecules is (in `km s^(-1)`)
View SolutionAt a pressure of `24 xx 10^(5) dynecm^(-2)`. The volume of `O_(2)` is `10 litre` and mass is `20 g`. The rms velocity will be
View SolutionThe temperature at which the root mean square velocity of the gas molecules would become twice of its value at `0^(@)C` is
View SolutionThe adjoining graph shows the distribution of kinetic energies `E_(k)` among the consultant molecules of a gas at a uniform temperature. `N` is the number of molecules each having energy in a small energy band around `E-(k)`. Which of the following statements is true?
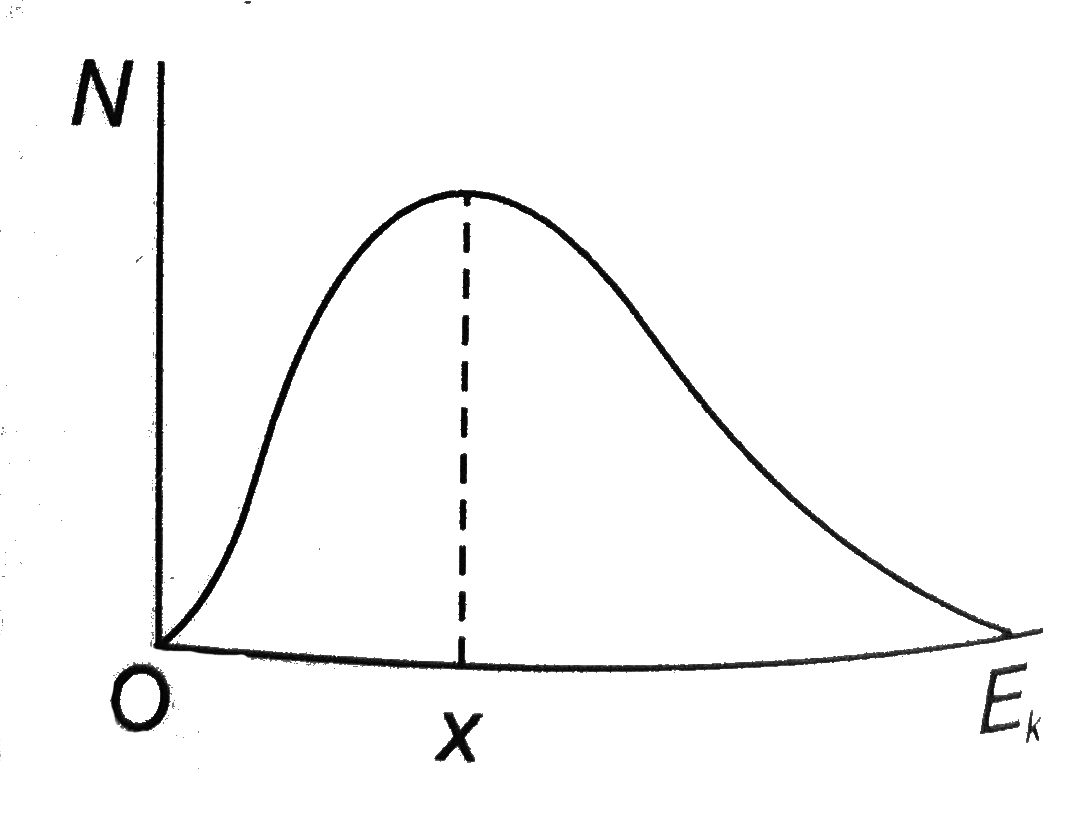
View SolutionAt identical temperatures, the rms speed of hydrogen molecules is `4` times that for oxygen molecules. In a mixture of these in mass ratio `H_(2) : O_(2) = 1 : 8`, the rms speed of all molecules in n times the rms speed for `O_(2)` molecules, where n is
View SolutionThe temperature at which rms velocity of helium molecules is equal to the rms velocity of hydrogen molecules at `NTP` is
View SolutionIf `P = 106 kT`, then the number of molecules per unit volume of the gas is [the letters have usual meanings.]
View SolutionN molecules , each of mass m, of gas A and 2 N molecules , each of mass 2m, of gas B are contained in the same vessel which is maintained at a temperature T. The mean square volcity of molecules of B type is denoted by ` V_(2)` and the mean square velocity of A type is denoted by `V_(1)` then `(V_(1))/(V_(2))` is
View SolutionThe pressure P, Volume V and temperature T of a gas in the jar A and the other gas in the jar B at pressure `2P`, volume `V//4` and temperature `2 T`, then the ratio of the number of molecules in the jar A and B will be
View SolutionAt what temperature is the root mean square velocity of gaseous hydrogen molecules is equal to that of oxygen molecules at `47^(@)C`?
View SolutionGas at a pressure `P_(0)` in contained as a vessel. If the masses of all the molecules are halved and their speeds are doubles. The resulting pressure P will be equal to
View SolutionThe root mean square speed of the molecules of a diatomic gas is v. When the temperature is doubled, the molecules dissociates into two atoms. The new root mean square speed of the atom is
View SolutionThe molecules of a given mass of gas have a rms velocity of `200 m//sec` at `27^(@)C` and `1.0 xx 10^(5) N//m^(2)` pressure. When the temperature is `127^(@)C` and pressure is `0.5 xx 10^(5) N//m^(2)` , the rms velocity in `m//sec` will be
View SolutionWhich of the following statement is true?
View SolutionAt which of the following temperatures would the molecules of a gas have twice the average kinetic energy they have at `20^(@)C`?
View SolutionA vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300K. The ratio of the average rorational kinetic energy per `O_2` molecules to that per `N_2` molecules is
View SolutionThree closed vessels `A, B` and `C` are at the same temperature T and contain gases which obey the Maxwellian distribution of velocities. Vessel A contains only `O_(2), B` only `N_(2)` and `C` a mixture of equal quantities of `O_(2)` and `N_(2)`. If the average speed of the `O_(2)` molecules in vessel `A` is `V_(1)`, that of the `N_(2)` molecules in vessel `B` is `V_(2)`, the average speed of the `O_(2)` molecules in vessel `C` is (where `M` is the mass of an oxygen molecules)
View SolutionIn a period of `1.00 s, 5 xx 10^(23)` nitrogen molecules strike a wall with an area of `8.00 cm^(2)`. Assume the molecules move with a speed of `300 m//s` and strike the wall head-on in elastic collisions. What is the pressure exerted on the wait?
Note : The mass of one `N_(2)` molecules is `4.65 xx 10^(-26) kg`
View SolutionTwo molecules of gas have speeds of `9 xx 10^(6) ms^(-1)` and `1 xx 10^(6) ms^(-1)` respectively. What is the root mean square speed of these molecules?
View SolutionThe molecules of a given mass of gas have root mean square speeds of `100 ms^(-1)` at `27^(@)C` and `1.00` atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at `127^(@)C` and `2.0` atmospheric pressure?
View SolutionTwo vessels A and B contain ideal gases with the temperature of B double that of A. Both gases are heated, so that they attain the same temperature. It is found that the fractional increase in the most probable speed of gas in vessel A is double that of the mean speed of gas in B. The ratio of the final to the initial temperature of gas in vessel A is
View SolutionThe rms speed of particle of mass `5 xx 10^(-17) kg`. In their random motion in air at NTP will be (Boltzmann's constant) `K = 1.38 xx 10^(-23) J//K`
View SolutionA light container having a diatomic gas enclosed with in is moving with velocity v. Mass of the gas is M and number of moles is n. The kinetic energy of gas w.r.t ground is
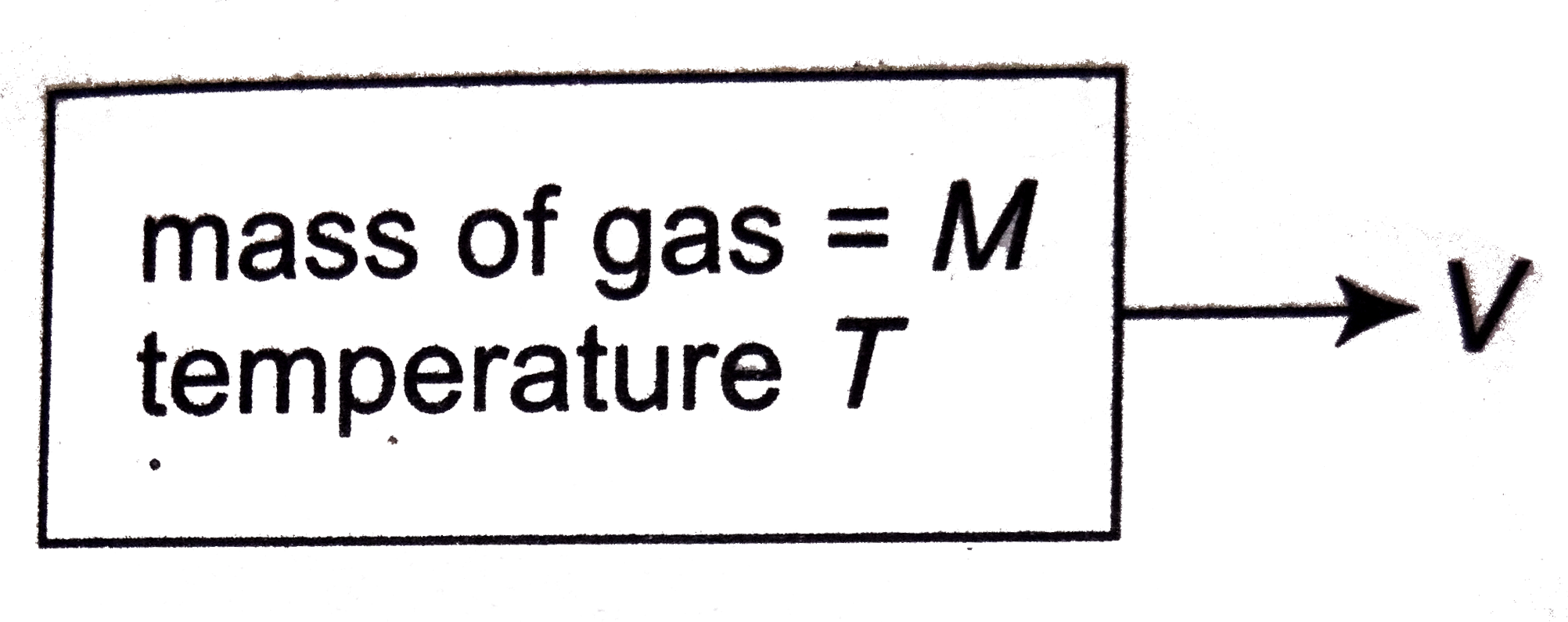
View SolutionA cylinder contains a mixture of helium and argon gas in equilibrium at `150^(@)C`. What is the average kinetic energy for each type of gas molecules?
View SolutionIn the previous equation, what is the rms speed of each type of molecules?
View SolutionCalculate the ratio of the mean free paths of the molecules of two gases having molecular diameters `1 Å` and `2 Å`. The gases may be considered under identical conditions of temperature, pressure and volume.
View SolutionAn insulated container containing monoatomic gas of molar mass s is moving with a velocity `v_0`. If the container is suddenly stopped, find the change in temperature.
View SolutionA spherical balloon of volume V contains helium at a pressure P. How many moles of helium are in the balloon if the average kinetic energy of the helium atoms is `vec(K)`?
View SolutionA spherical balloon of volume `4.00 xx 10^(3) cm^(3)` contains helium at a pressure of `1.20 xx 10^(5) Pa`. How many moles of helium are in the balloon if the average kinetic energy of the helium atoms is `3.60 xx 10^(-22) J`?
View Solution
Kinetic Theory Of Gases questions and complete solutions for chapter KINETIC THEORY OF GASES AND THERMODYNAMICS of A2Z PHYSICS (HINGLISH) of Class 11