Complete Solutions to Practice exercise of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| BITSAT GUIDE | Practice exercise |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
Calculate the gravitational force of attraction between two spherical bodies, each of mass 1kg placed at 10m apart `(G = 6.67 xx 10^(-11)Nm^(2)//kg^(2))`.
View SolutionIf the distance between two masses is doubled, then the gravitational attraction between them will be
View SolutionHow the gravitational constant will change if a brass plate is introduced between two bodies ?
View SolutionSix particles each of mass`m` are placed at the corners of a regular hexagon of edge length `a`. If a point mass `m_0` is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View SolutionTwo particles each of mass 'm' are placed at `A` and `C` are such `AB=BC=L`. The gravitational force on the third particle placed at `D` at a distance `L` on the perpendicular bisector of the line `AC` is
View SolutionIn a hypothetical concept, electron of mass `m_(e)` revolves around nucleus due to gravitational force of attraction between electron and proton of mass `m_(p)`. If the radius of circular path of electron is r, then the speed of electron is
View SolutionThree point masses each of mass `m` rotate in a circle of radius `r` with constant angular velocity `omega` due to their mutual gravitational attraction. If at any instant, the masses are on the vertices of an equilateral triangle of side `a`, then the value of `omega` is
View SolutionA gravitational field is present in a region. A point mass is shifted from `A` to `B`, along different paths shown in the figure. If `W_1, W_2` and `W_3` represent the work done by gravitational force for respective paths, then
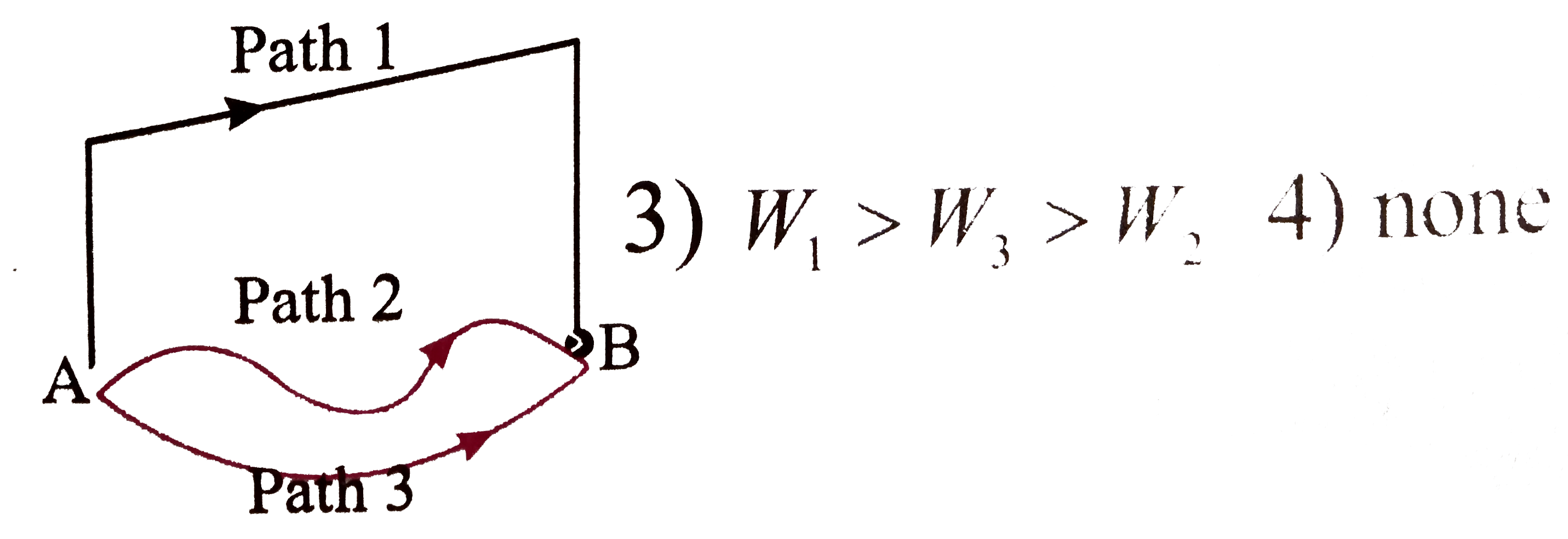
View SolutionA point mass `m_(0)` is placed at distance `R//3` from the centre of spherical shell of mass m and radius R. the gravitational force on the point mass `m_(0)` is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of `d = sqrt(3)R` from the centre of the sphere. The gravitational attraction between the sphere and the ring is
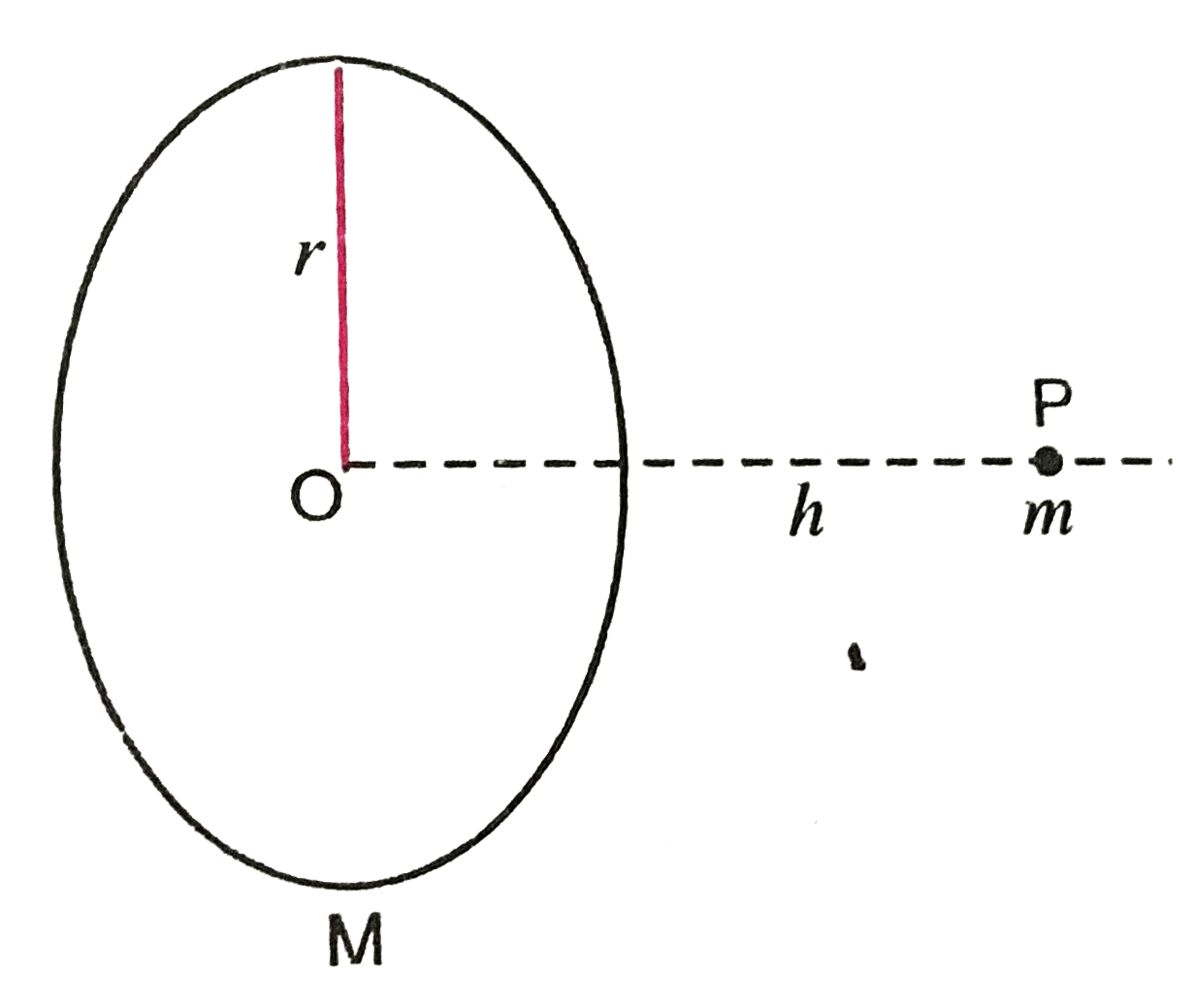
View SolutionA mass `m` is placed at `P` a distance `h` along the normal through the centre `O` of a thin circular ring of mass `M` and radius `r` Fig.
If the mass is removed futher away such that `OP` becomes `2h`, by what factor the force of gravitational will decrease, if `h = r` ?
View SolutionA point mass of 10 kg is placed at the centre of earth. The weight of the point mass is
View SolutionHow will you weight the sun, i.e. estimate its mass ? You will need to know the period of one of its planets and the radius of the planetary orbit. The mean orbit radius of the earth around the sun is `1.5 xx 10^(8)km`, then the mass of the sun would be calculated as
View SolutionA particle hanging from a massless spring stretches it by `2 cm` at the earth's surface. How much will the same particle stretch the spring at a height Of `2624Km` from the surface of the earth? (Radius of the earth`=6400 km`)
View SolutionThere is a mine of deoth 2km. The conditions as compared to those at the surface of the earth are
View SolutionIn order to make the weight of a 5kg body to zero at the equator. The angular speed of the earth would must be (take, `g = 10m//s^(2)` and radius of the earh, `R = 6400 km)`
View SolutionAt what height, the weight of the body is same as that at same depth from the earth's surface (take, earth's radius = R)
View SolutionAt the surface of a certain planet acceleration due to gravity is one - quarter of that on earth If a brass ball is transported to this planet , then which one of the following statements is not correct ? .
View SolutionIf both the mass and radius of the earth, each decreases by 50%, the acceleration due to gravity would
View SolutionA body is suspended on a spring balance in a ship sailing along the equator with a speed v'. If `omega` is the angular speed of the earth and `omega_(0)` is the scale reading when the ship is at rest, the scale reading when the ship is sailing is
View SolutionThe maximum vertical distance through which a full dressed astronaut can jump on the earth is 0.5m. Estimate the maximum vertical distance through which he can jump on the motion, which has a mean density 2/3 rd that of the earth and radius one-quarter that of the earth.
View SolutionTwo stallites A and B revolve round the same planet in coplanar circular orbits lying in the same plane. Their periods of revolutions are 1h and 8h, respectively. The radius of the orbit of A is `10^(4)`km. The speed of B relative to A when they are closed in `kmh^(-1)` is
View SolutionA satellite is moving on a circular path of radius r around earth has a time period T. if its radius slightly increases by `Deltar`, determine the change in its time period.
View SolutionThe gravitational field in a region is `10N//kg (hati - hatj)`. Find the work done by gravitational force to shift slowly a particle of mass 1kg from point (1m, 1m) to a point (2m,-2m).
View SolutionIn previous problem, find the work done by external agent.
View SolutionThe gravitational force in a region is given by, `vec(F)=mayhati+maxhatj` The work done by gravitational force to shift a point mass `m` from `(0,0,0)` is `(x_(0),y_(0),z_(0))` is
View SolutionThe work done by an external agent to shift a point mass from infinity to the centre of the earth is `W`. Then choose the correct relation.
View SolutionThe work done liftting a particle of mass 'm' from the centre of the earth to the surface of the earth is
View SolutionThe change in the gravitational potential energy when a body of a mass `m` is raised to a height `nR` above the surface of the earth is (here `R` is the radius of the earth)
View SolutionSuppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
View SolutionThe time period of a simple pendulum at the centre of the earth is
View SolutionIf a rocket is fired with a velocity, `V=2sqrt(gR)` near the earth's surface and goes upwards, its speed in the inter-stellar space is
View SolutionIf the satellite is stopped suddenly in its orbit which is at a distnace = radius of earth from earth’s surface and allowed to fall freely into the earth, the speed with which it hits the surface of earth will be -
View SolutionA projectile is fired vertically upwards from the surface of the earth with a velocity `Kv_(e)`, where `v_(e)` is the escape velocity and `Klt1`.If `R` is the radius of the earth, the maximum height to which it will rise measured from the centre of the earth will be (neglect air resistance)
View SolutionA satellite of mass M revolving in a circular orbit of radius `r_(s)` around the earth of mass M has a total energy E. then, its angular momentum will be
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

View SolutionTwo bodies each of mass 1kg are at a distance of 1m. The escape velocity of a body of mass 1 kg which is midway between them is
View SolutionThe artifical satellite is moving in a circular around the earth with a speed equal to half the magnitude of escape velocity from the earth. (i) Determine the height of the satellite above the earth's surface, (ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely on to the earth , find the speed with which it hits surface of the earth. Take`g=9.8ms^(-2)`, radius of the earth =6400km.
View SolutionA particle of mass m is projected from the surface of earth with a speed `V_(0)(V_(0) lt` escape velocity). Find the speed of particle at height `h = R` (radius of earth). (Take, `R = 6400 km` and `g = 9.8 m//s^(2))`
View SolutionThe binding energy of earth-sun system is (neglecting the other planets)
View SolutionOne of the satellite of jupiter, has an orbital period of `1.769` days and the radius of the orbit is `4.22 xx 10^(8) m`. Show that mass of jupiter is about one thousandth times that of the mass of the sun. (Take `1` year `= 365.15` mean solar day).
View SolutionA satellite is orbiting closely to earth and having kinetic energy K. the kinetic energy required by it to just overcome the gravitational pull of the earth, is
View Solution
Practice exercise questions and complete solutions for chapter GRAVITATION of BITSAT GUIDE PHYSICS (HINGLISH) of Class 11