Complete Solutions to Practice Exercise of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| BITSAT GUIDE | Practice Exercise |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
A particle executing simple harmonic motion has amplitude of `1 m` and time period `2 s` at `t = 0`, net force on the particle is zero. Find the equation of displacement of the particle.
View SolutionIn the previous question, find maximum velocity and maximum acceleration.
View SolutionA particle executes simple harmonic motion. The amplitude of vibration of particle is 2 cm. The displacement of particle in one time period is
View SolutionThe distance travelled by the particle is
View SolutionA particle move along y-axis according to equation `y =3+4 cos omega t`. The motion of the particle is
View SolutionIn the amplitude of vibration is
View SolutionIf s=a `sinomegat hati+b cos omegat hatj`, the equation of path of particle is
View SolutionIn previous question, the amplitude of vibration is
View SolutionThe motion of a particle varies with time according to the relation `y=a (sinomegat + cos omegat)` ,then
View SolutionA particle executes SHM along a straight line so that its period is 12 s. The time it takes in traversing a distance equal to half its amplitude from its equilibrium position is
View SolutionA particle executes `SHM` with an amplitude of `10cm` and frequency `2 Hz`. At `t = 0`, the particle is at a point where potential energy and kinetic energy are same. The equation for its displacement is
View SolutionA particle executes simple harmonic motion with a frequency f. The frequency with which the potential. Energy oscillates is
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is `V(x) = k|x|^3` where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle free to move along the (x - axis) hsd potential energy given by `U(x)= k[1 - exp(-x^2)] for -o o le x le + o o`, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA simple harmonic oscillator has amplitude A, angular velocity `omega`, and mass m . Then, average energy in one time period will be
View SolutionA point mass x = 20 kg, is suspended by a massless spring of constant 2000 N/m. The point mass is released when elongation in the spring is 15 cm. The equation of displacement of particle as function of time is (take, g =`10m//s^(2)`)

View SolutionA spring of spring constant `200N//m` has a block of mass `1kg` hanging at its one end and other end of spring is attached to ceiling of an elevator. The elevator is rising upwards with an acceleration `g//3`. What should be the angular frequency and elongation during the time when the elevator is accelerating?
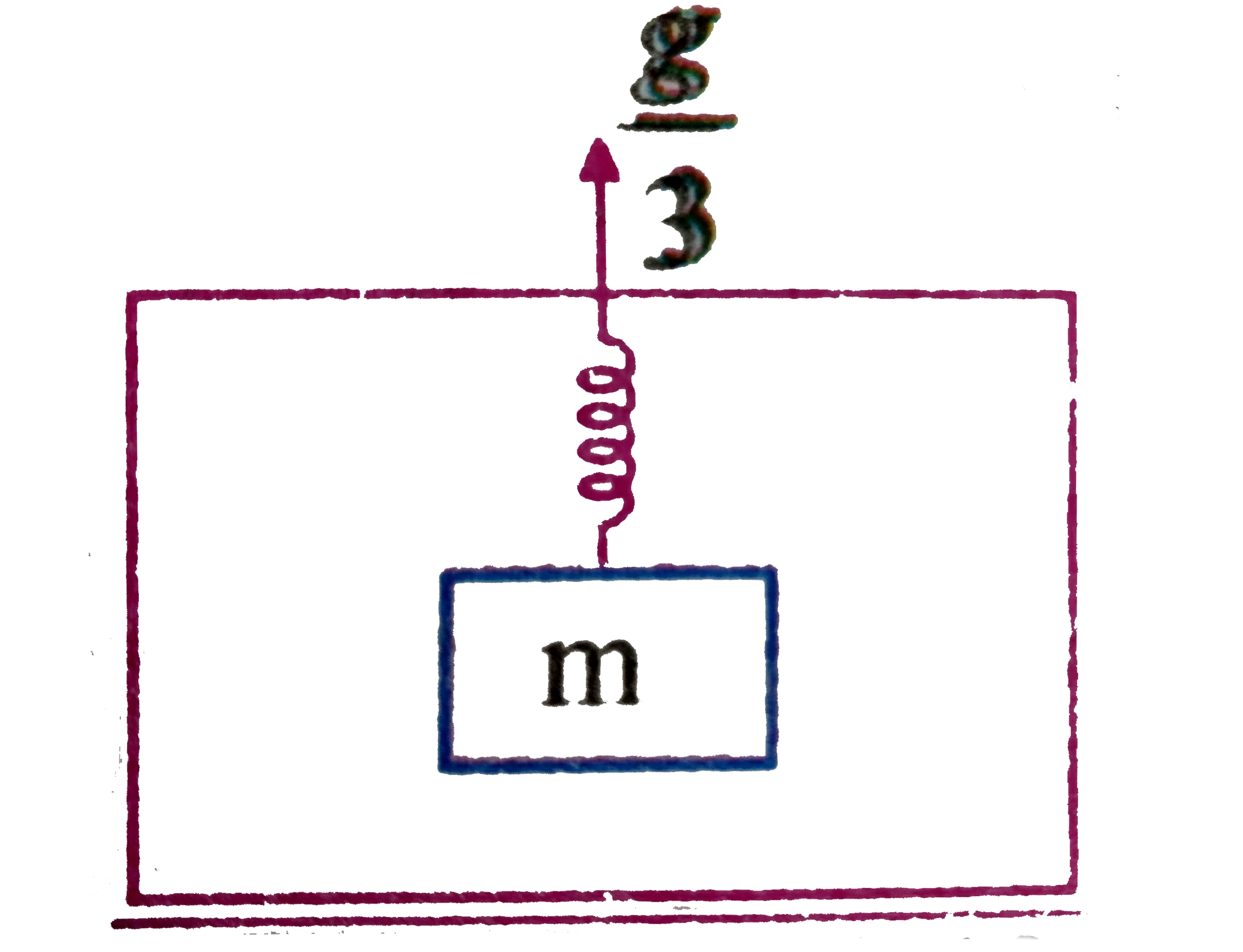
View SolutionA spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then the long piece will have a force constant of
View SolutionA solid copper sphere is suspended from a massless spring. The time period of oscillation of the system is 4 s. The sphere is now completely immersed in a liquid whose density is 1/8the that of brass. The sphere remains in liquid during oscillation. Now, the time period is
View SolutionA load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is

View Solutionfind the amplitude of vibration.
View SolutionTwo point masses of `3.0kg` and `1.0kg` are attached to opposite ends of a horizontal spring whose spring constant is `3Nm^(-1)` as shown in figure . The natural frequency of vibration so this system is `n//piHz`. Find the integral value of `n`.

View Solution
Two blocks connected by a spring rest on a smooth horizontal plane as shown in Fig. A constant force `F` start acting on block `m_2` as shown in the figure. Which of the following statements are not correct?
View SolutionThere is a spring with netural length `L_(0)`. Two masses `m_(1)` and `m_(2)` are connected to both of its ends as shown in figure. The whole system is held at rest. At any time `t =0, m_(2)` is released and system starts free fall. Initial stretched length of spring before fall is `L.` what is the displacement of centre of mass as function of time?
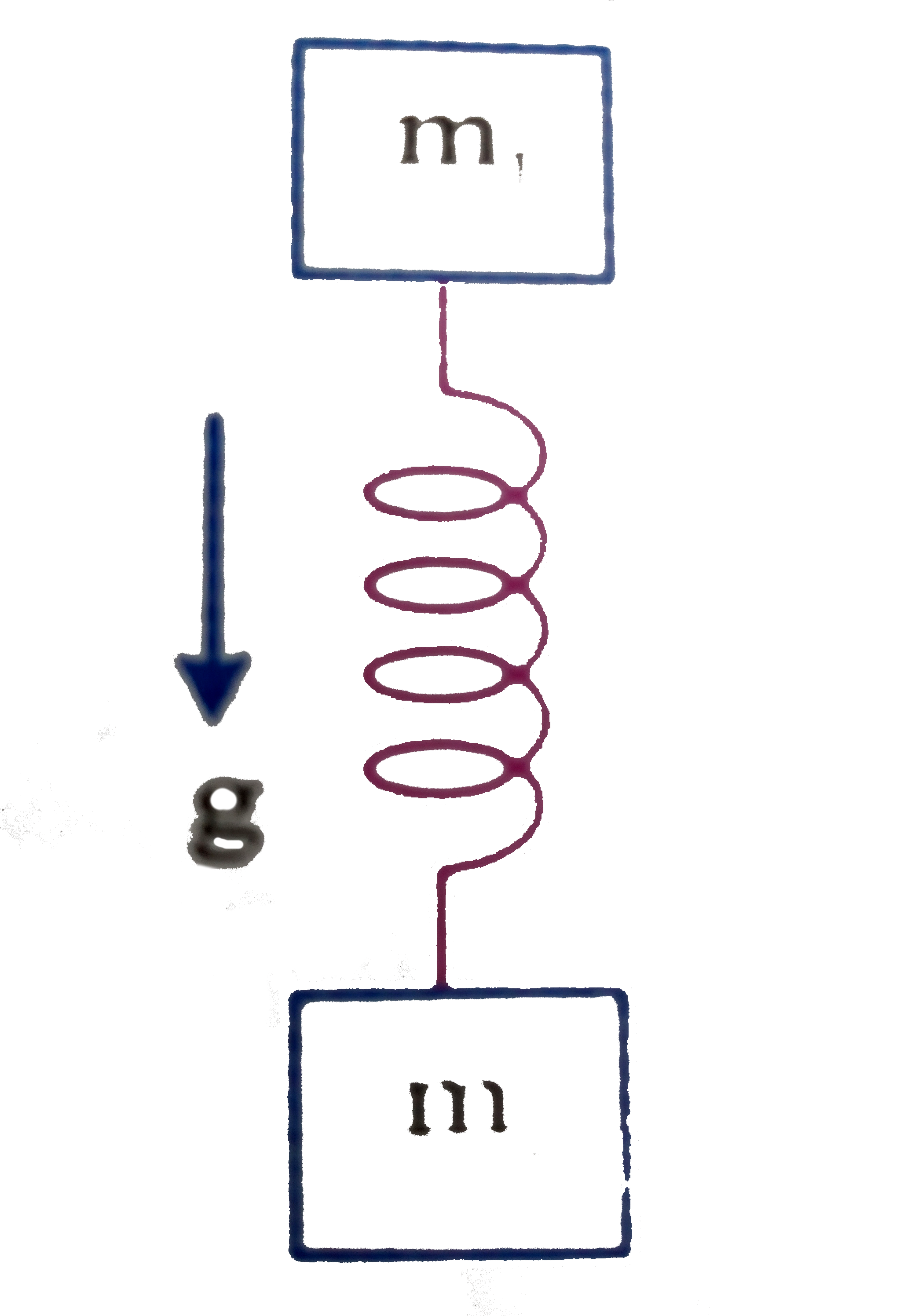
View SolutionThe time period of a second’s pendulum is 2 sec. The spherical bob which is empty from inside has a mass of 50 gm. This is now replaced by another solid bob of same radius but having different mass of 100 gm. The new time period will be
View SolutionA clock pendulum is adjusted for giving corrent time in Patna. This clock pendulum also givens correct time in
View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit `-phi` and `+phi`. For an angular displacement `theta(|theta|ltphi)`, the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
View SolutionFrom the ceiling of a train, a pendulum of length 'l' is suspended. The train is moving with an acceleration `a_(0)` on horizontal surface. What must be the period of oscillation of pendulum?
View SolutionA clock with an iron pendulum keeps correct time at `20^(@)C`. How much time will it lose or gain in a day if the temperature changes to `40^(@)C`. Thermal coefficient of liner expansion `alpha = 0.000012 per^(@)C`.
View SolutionThere are two pendulums of length `l_(1)` and `l_(2)` start vibrating. At some instant, the two are in mean position in the same phase. Calculate after how many vibrations of shorter pendulum, the two wll be in phase in the mean position?
`[(l_(1)gtl_(2)),l_(1)=121cm, l_(2)=100cm]`
View SolutionA clock is performing SHM along a vertical line with amplitude of 40 cm on a horizontal plank. The block just lose the contact with plank when plank is momentarily at rest. Then, (Take, `g=10m//s^(2)`)
View SolutionThere is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
View SolutionThere is a rod of length `l` and mass `m`. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA particle of mass `m` is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton `x^(2) =4ay`. The angular frequency of small oscillation is given by
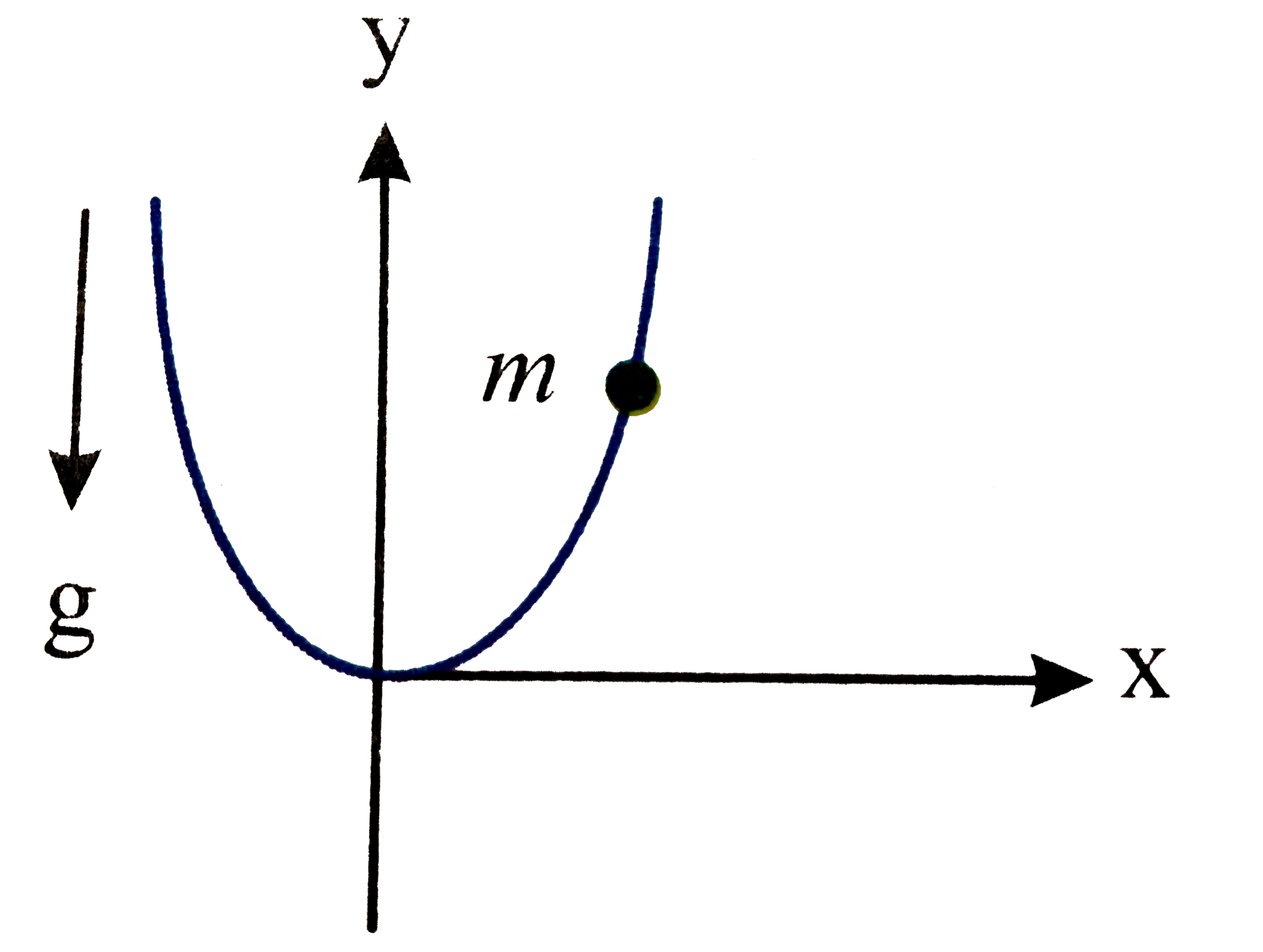
View SolutionA highly rigid cubical block `A` of small mass `M` and side `L` is fixed rigidly on the other cubical block of same dimensions and of modulus of rigidity `eta` such that the lower face of `A` completely covers the upper face of `B`. The lower face of `B` is rigidly held on a horizontal surface . `A` small force `F` is applied perpendicular to one of the side faces of `A`. After the force is withdrawn , block `A` executes faces of `A`. After the force is withdrawn , block `A` exceutes small oscillations , the time period of which is given by
View SolutionA cylinder piston of mass `M` sides smoothlly inside a long cylinder closed at and enclesing a cartin mass of gas The cylinder is kept with its axis horizantal if the pistan is distanced from its equations positions it oscillation simple harmoniically .THe period of oscillation will be

View Solution
Practice Exercise questions and complete solutions for chapter SIMPLE HARMONIC MOTION of BITSAT GUIDE PHYSICS (HINGLISH) of Class 11