Complete Solutions to Practice Exercise of chapter MAGNETOSTATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MAGNETOSTATICS |
| BITSAT GUIDE | Practice Exercise |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Calculate the force acting between two small magnets, placed in end on position `0.1 m` apart from their centres. (Given, magnetic moment of each magnet is `5 Am^(2)`).
View SolutionTwo similar equal magnetic poles when separated by a distance of `1 m`,
View SolutionThree similar magnetic south poles each of streright `10 Am` are placed at the corners of an equallateral triangle of side `20 cm`. Find the magnetic force on one of the pole.
View SolutionSix s imilar magnetic poles are placed on six corners of a regular hexagon of side `10 cm`. A south pole of strength `10 Am` is placed at the centre of hexagon. Find the magnetic force on the south pole.
View SolutionA magnetic wire of dipole moment `4pi Am^(2)` is bent in the form of semicircle. The new magnetic moment is
View SolutionA current I flows in a conducting wire of lenth L. If we bent it in a circular form, then calculate its magnetic dipole moment.
View SolutionThe magnetic induction inside a solenoid is `6.5xx10^(-4)T`. When it is filled with iron medium, then the induction becomes `1.4 T`. The relative permeability of iron will be
View SolutionIf a magnetising field of `1600 A//m` produces a magnetic flux of `14xx10^(-5) Wb` in an iron bar of cross-sectional area `0.2 cm^(2)`. Then,
View SolutionTwo dissimilar poles of strength `x mWb` and `2 mWb` are sparated by a distance `12 cm`. If the null point is at a distance of a `4 cm` fro `2 mWb`, then calculate `x`.
View SolutionTwo small magnets of each of magnetic moment `M_(0)` is placed parallel to each other (show in figure). The magnetic field at point `O` is

View SolutionTwo short magnets of magnetic moment `2 Am^(2)` and `5 Am^(2)` are placed along two lines drawn at right angle to each other on the sheet of paper as shown in the figure. What is the magnetic field at the point of intersection of their axis?

View SolutionCalculate the magnetic induction at P, for the arrangement shown in figure, when two similar short magnets of magnetic moment M are joined at the middle. So that they are mutually perpendicular -
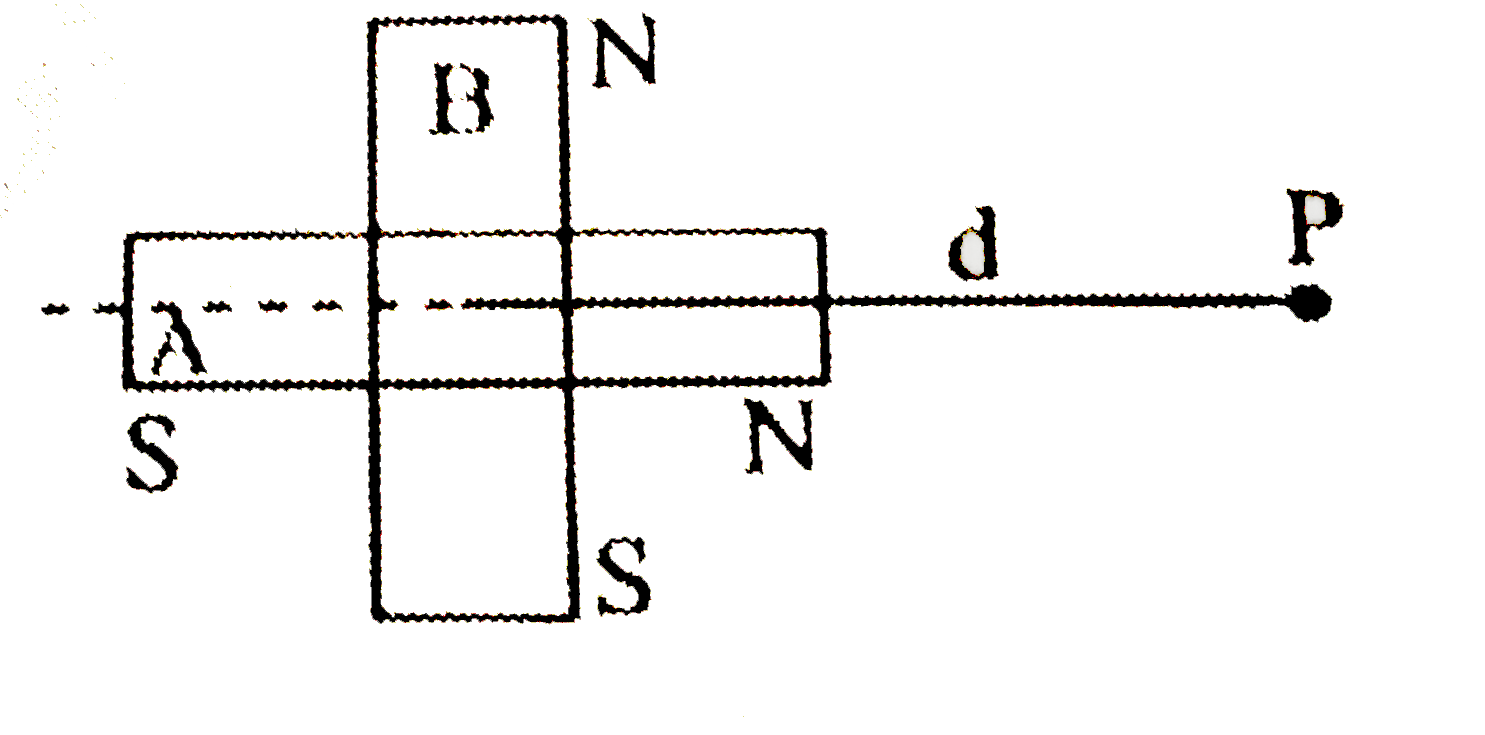
View SolutionA small magnet of dipole moment `M` is kept on the arm of a deflection magentometer set in tan `A` position at a distance of `0.2 m`. If the deflection is `60^(@)`, find the value of `P (B_(H)=0.4xx10^(-4)T)`.
View SolutionA short bar magnet of moment `0*32JT^-1` is placed in a uniform external magnetic field of `0*15T`, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
View SolutionA magnet of dipole moment `2Am^(2)` is deflected through `30^(@)` from magnetic meridian. The required deflecting torque is `(B_(H)=0.4xx10^(-4)T)`
View SolutionIf the areas under the `I-H` hysteresis loop and `B_H` hysteresis loop are denoted by `A_(1)` and `A_(2)`, then
View SolutionConsider the plane S formed by the dipole axis and the axis of earth. Let P be point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators Obtain the declination and dip angles at P and Q.
View SolutionA magnet of length `14 cm` and magnetic moment `mu` is broken into two parts of length 6 cm and 8 cm. They are put at right angles to each other with the opposite poles togather. The magnetic dipole moment of the combination is:
View SolutionA uniform magnetic needle of strength of each pole is `98.1 amp, cm`, is suspended from its centre by a thread. When a mass of `50 mg` is loaded to its upper end, the needle becomes horizontal, then the vertical component of earth's magnetic induction is `(g=981 cm//s^(2))`
View SolutionTwo short bar magnets of dipole moments M and `Msqrt(3)` are joined at right angles to form a cross as depicted in the figure . The value of `theta` for which the system remains in equilibrium in a uniform external magnetic field B, is
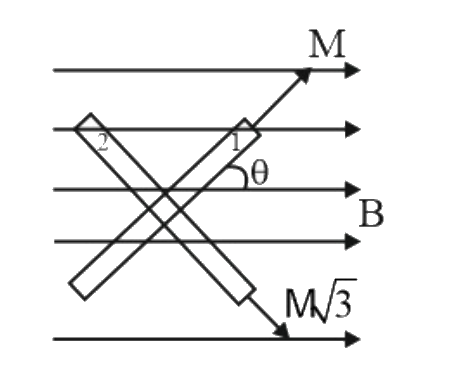
View SolutionThe couple acting on a magnet of length 10cm and pole strength 15A-m, kept in a field of `B=2xx10^(-5)`, at an anlge of `30^(@)` is
View SolutionA bar magnet has a magnetic moment `2.5JT^(-1)` and is placed in a magnetic field of `0.2 T`. Calculate the work done in turning the magnet from parallel to antiparallel position relative to field direction.
View SolutionTwo like poles of strengths `m_(1)` and `m_(2)` are at far distance apart. The energy repuired to bring them `r_(0)` distance apart is
View SolutionCalculate the work done in deflecting a small magnet of magnetic moment `10Am^(2)` through `180^(@)` from a uniform magnetic field of strength `0.4 xx 10^(-4)T`.
View SolutionAt a place the value of `B_(H)` and `B_(V)` are `0.4xx10^(-4)T` and `0.3xx10^(-4)T` respectively. The resultant earth's magnetic field is
View SolutionIn previous problem, the angle of dip is
View SolutionThe real angle of dip, if a magnet is suspended at an angle of `30^(@)` to the magnetic meridian and the dip needle makes an angle of `45^(@)` with horizontal, is:
View SolutionA magnet is cut in three equal parts by cutting it perpendicular to its length. The time period of original magnet is `T_0` in a uniform magnetic field B. Then, the time period of each part in the same magnetic field is
View SolutionA magnet is cut in three equal parts by cutting it perpendicular to its length. The time period of original magnet is `T_0` in a uniform magnetic field B. Then, the time period of each part in the same magnetic field is
View SolutionThe current on the winding of a toroid is 2 A. It has 400 turns and mean circumferential length is 40 cm. With the help of search coil and charge measuring instrument the magnetic field is found to be 1 T. The susceptibility is
View SolutionThe magnetic needle of a tangent galvanometer is deflected at an angle `30^(@)` due to a magnet. The hoeizontal component of earth's magnetic field `0.34xx10^(-4)T` is along the plane of the coil. The magnetic intensity is
View SolutionCalculate the angle of dip, if a dip needle oscillating in a vertical plane makes 40 oscillations per minute in a magnetic meridian and 30 oscillations per minute in a vertical plane at right angle to the magnetic meridian.
View SolutionInside a long solenoid wounded with 300 turns/m, an iron rod is placed. An iron rod is 0.2 m long, 10 mm in diameter and of permeability `10^(3)`. Calculate the magnetic moment of the rod, if 0.5 A of current is passed through the rod.
View SolutionAn iron rod is subjected to cycles of magnetisation at the rate of `50Hz`. Given the density of the rod is `8xx10^(3)kg//m^(3)` and specific heat is `0.11xx10^(-3)calxxkg^(@)C`. The rise in temperature per minute, if the area enclosed by the `B-H` loop corresponds to energy of `10^(-2)J` is (Assume there is no radiation losses)
View Solution
Practice Exercise questions and complete solutions for chapter MAGNETOSTATICS of BITSAT GUIDE PHYSICS (HINGLISH) of Class 11