Complete Solutions to Exercises (Linked Comprehensive) of chapter STATES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | STATES OF MATTER |
| CENGAGE CHEMISTRY | Exercises (Linked Comprehensive) |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
The figure given below shows three glass chambers that are connected by valves of negligible volume. At the outset of an experiment, the valves are closed and the chambers contain the gases as detailed in the diagram. All the chambers are at the temperature of `300 K` and external pressure of `1.0 atm`.
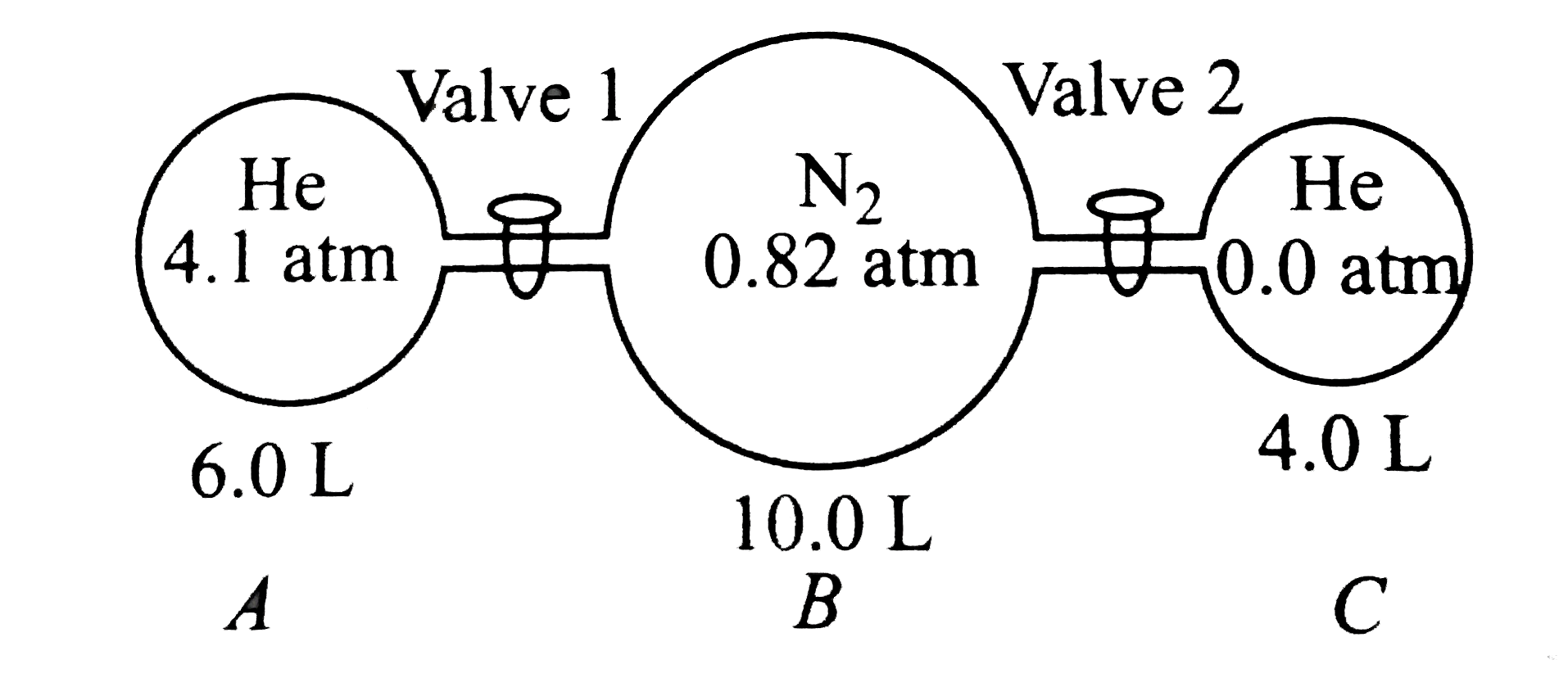
What will be the work done by `N_(2)` gas when valve `2` is opened and value `1` remains closed?
View SolutionThe figure given below shows three glass chambers that are connected by valves of negligible volume. At the outset of an experiment, the valves are closed and the chambers contain the gases as detailed in the diagram. All the chambers are at the temperature of `300 K` and external pressure of `1.0 atm`.

Which of the following represents the total kinetic energy of all the gas molecules after both valves are opened?
(`R=0.082 atm L K^(-1) mol^(-1)=8.314 JK^(_1)mol^(-1)`)
View SolutionThe figure given below shows three glass chambers that are connected by valves of negligible volume. At the outset of an experiment, the valves are closed and the chambers contain the gases as detailed in the diagram. All the chambers are at the temperature of `300 K` and external pressure of `1.0 atm`.
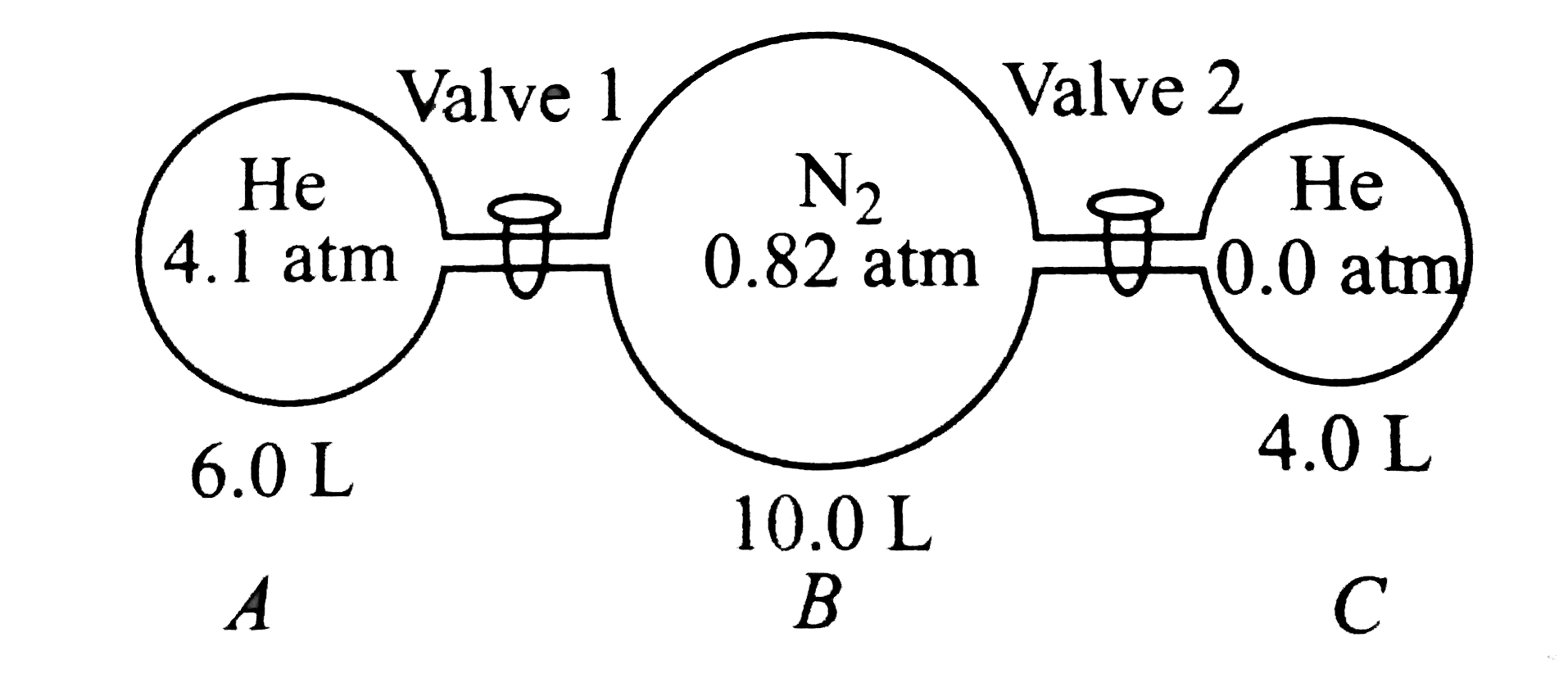
What is the total pressure in chamber `B` after valve `1` is opened?
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature `T` is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
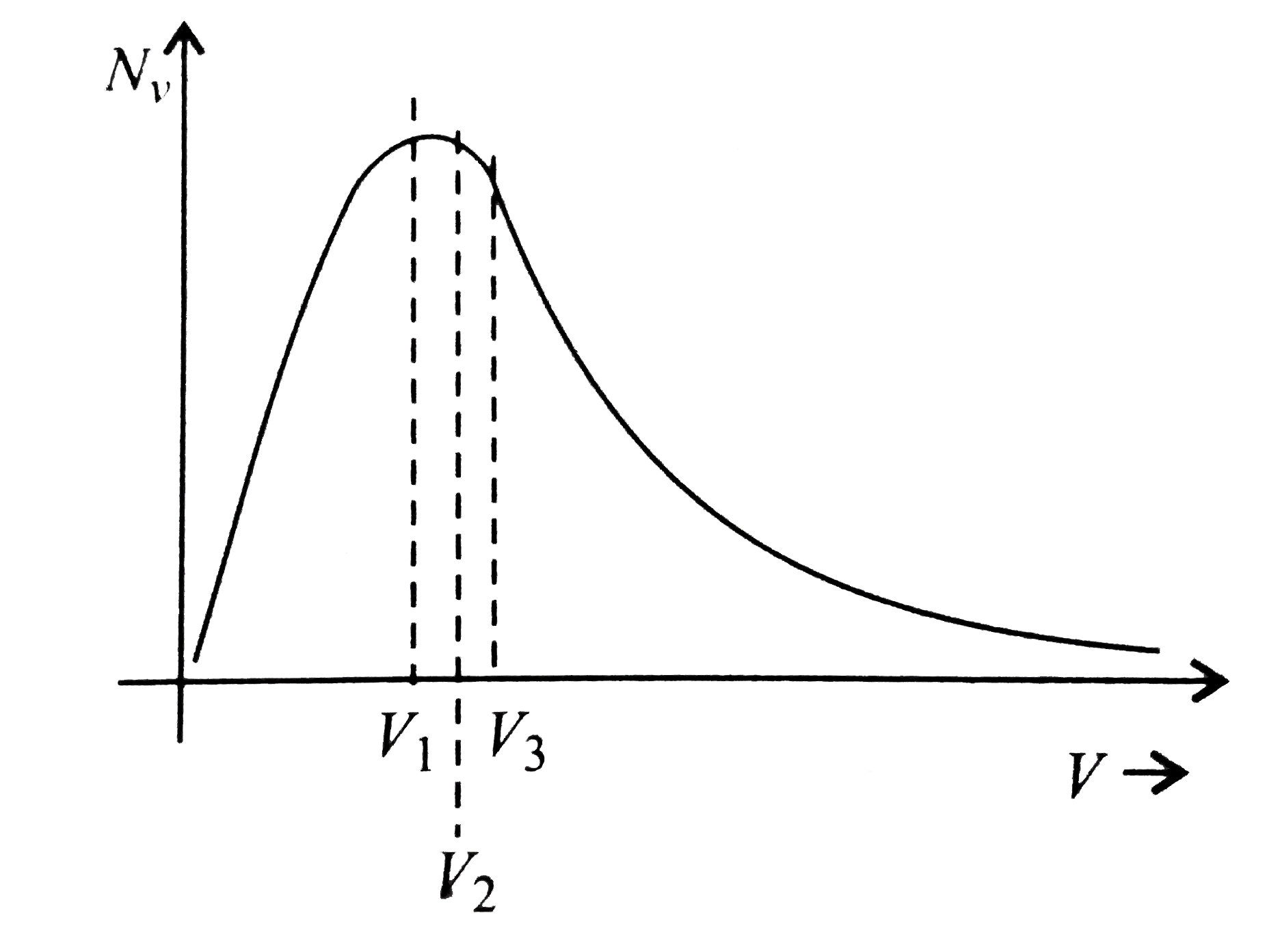
where
`v` is molecular velocity
`n` is number of molecules having velocity `v`
Let us define `Delta N_(v)`, which is equal to the number of molecules between the velocity range `v` and `v+ Delta v`, given by
`Delta N_(v)=4piNa^(3)e^(-bv^(2))v^(2)Deltav`
where
`N` is total number of molecules
`a=sqrt((M_(0))/(2piRT))` and `b=(M_(0))/(2RT)`
`R` is universal gas constant
`T` is temperature of the gas
`M_(0)` is molecular weight of the gas
Answer the following question:
`SI` units of `a` are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature `T` is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
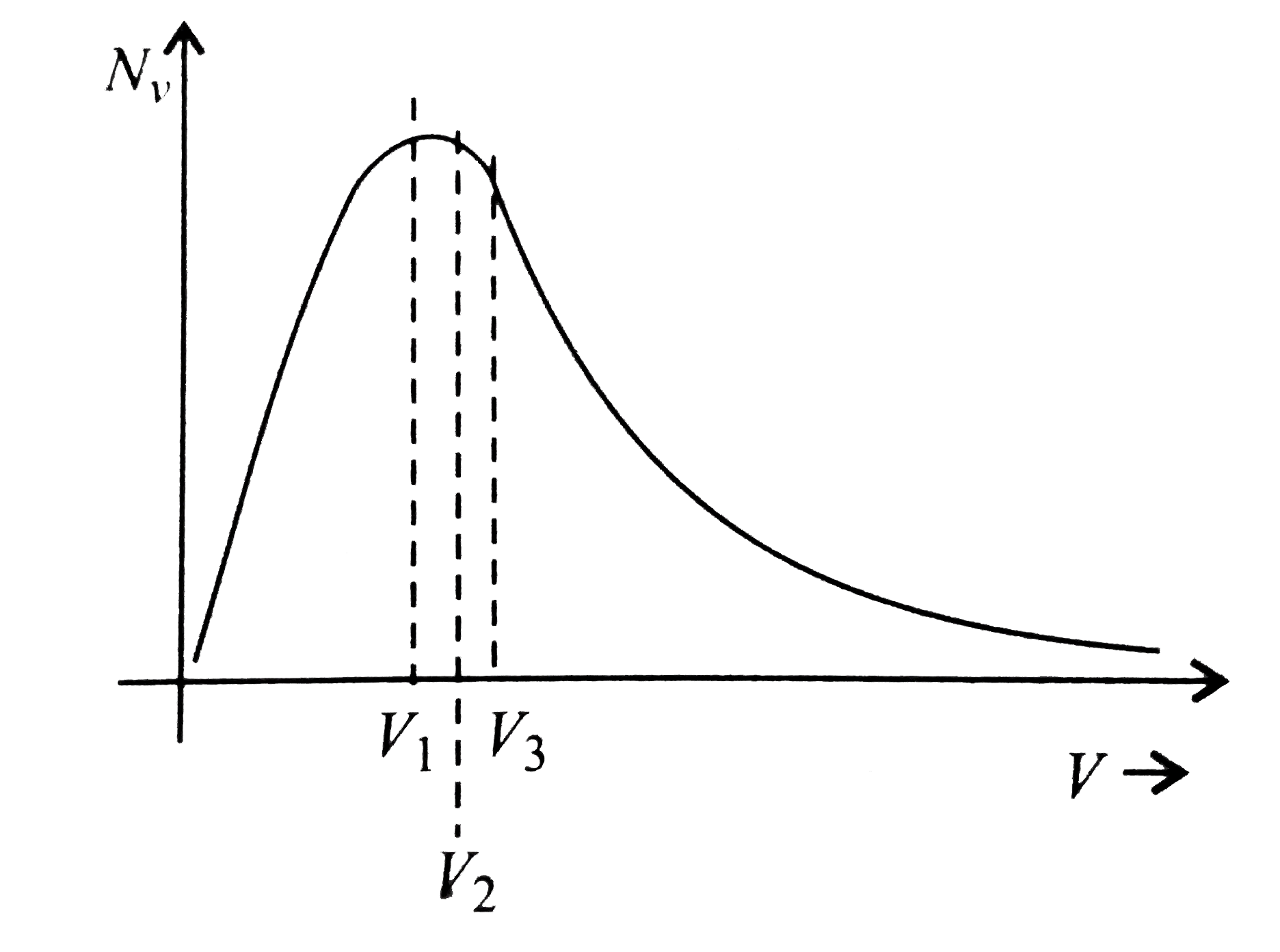
where
`v` is molecular velocity
`n` is number of molecules having velocity `v`
Let us define `Delta N_(v)`, which is equal to the number of molecules between the velocity range `v` and `v+ Delta v`, given by
`Delta N_(v)=4piNa^(3)e^(-bv^(2))v^(2)Deltav`
where
`N` is total number of molecules
`a=sqrt((M_(0))/(2piRT))` and `b=(M_(0))/(2RT)`
`R` is universal gas constant
`T` is temperature of the gas
`M_(0)` is molecular weight of the gas
Answer the following question:
`SI` units of `b` are
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature `T` is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
`v` is molecular velocity
`n` is number of molecules having velocity `v`
Let us define `Delta N_(v)`, which is equal to the number of molecules between the velocity range `v` and `v+ Delta v`, given by
`Delta N_(v)=4piNa^(3)e^(-bv^(2))v^(2)Deltav`
where
`N` is total number of molecules
`a=sqrt((M_(0))/(2piRT))` and `b=(M_(0))/(2RT)`
`R` is universal gas constant
`T` is temperature of the gas
`M_(0)` is molecular weight of the gas
Answer the following question:
If `(P)/(P_(c))=P_(r)`, `(T)/(T_(c))=T_(r)`, and `(V_(m))/(V_(m,c))=V_(r)` where
View SolutionTwo flasks `A` and `B` have equal volume. `A` is maintained at `300 K` and `B` at `600 K`. While `A` contains `H_(2)` gas, `B` has an equal mass of `CH_(4)` gas. Assuming ideal behaviours for both the gases, answer the following:
Flask containing greater number of molecules
View SolutionTwo flasks `A` and `B` have equal volume. `A` is maintained at `300 K` and `B` at `600 K`. While `A` contains `H_(2)` gas, `B` has an equal mass of `CH_(4)` gas. Assuming ideal behaviours for both the gases, answer the following:
Flask in which pressure is higher
View SolutionTwo flasks `A` and `B` have equal volume. `A` is maintained at `300 K` and `B` at `600 K`. While `A` contains `H_(2)` gas, `B` has an equal mass of `CH_(4)` gas. Assuming ideal behaviours for both the gases, answer the following:
Flask in which the compressibility factor is greater
View SolutionTwo flasks `A` and `B` have equal volume. `A` is maintained at `300 K` and `B` at `600 K`. While `A` contains `H_(2)` gas, `B` has an equal mass of `CH_(4)` gas. Assuming ideal behaviours for both the gases, answer the following:
Flask in which the total kinetic energy is greater
View SolutionTwo flasks `A` and `B` have equal volume. `A` is maintained at `300 K` and `B` at `600 K`. While `A` contains `H_(2)` gas, `B` has an equal mass of `CH_(4)` gas. Assuming ideal behaviours for both the gases, answer the following:
Flask with greater molar kinetic energy
View SolutionTwo flasks `A` and `B` have equal volume. `A` is maintained at `300 K` and `B` at `600 K`. While `A` contains `H_(2)` gas, `B` has an equal mass of `CH_(4)` gas. Assuming ideal behaviours for both the gases, answer the following:
Flask in which molecules are moving faster
View SolutionThe van der Waals constant for gases `A`, `B`, and `C` are as follows

Answer the following:
Which gas has the highest critical temperature?
View SolutionThe van der Waals constant for gases `A`, `B`, and `C` are as follows

Answer the following:
Which gas has the largest molecular volume?
View SolutionThe van der Waals constant for gases `A`, `B`, and `C` are as follows

Answer the following:
Which gas has the most ideal behaviour around `STP`?
View SolutionFor the given ideal gas equation `PV=nRT`, answer the following questions:
In the above equation, the value of universal gas constant depends only upon
View SolutionFor the given ideal gas equation `PV=nRT`, answer the following questions:
At constant temperature, in a given mass of an ideal gas
View SolutionFor the given ideal gas equation `PV=nRT`, answer the following questions:
Which of the following does not represent ideal gas equation?
View SolutionFor the given ideal gas equation `PV=nRT`, answer the following questions:
An ideal gas will have maximum density when
View SolutionFor the given ideal gas equation `PV=nRT`, answer the following questions:
which of the following is incorrect according to the ideal gas equation?
View SolutionUsing van der Waals equation `(P+(a)/(V^(2)))(V-b)=RT`, answer the following questions:
The van der Waals equation explains the behaviour of
View SolutionUsing van der Waals equation `(P+(a)/(V^(2)))(V-b)=RT`, answer the following questions:
The term that accounts for intermolecular forces in the van der Waals equation for non-ideal gas is
View SolutionUsing van der Waals equation `(P+(a)/(V^(2)))(V-b)=RT`, answer the following questions:
The term that accounts for effective volume in the van der Waals equation for non-ideal gas is
View SolutionUsing van der Waals equation `(P+(a)/(V^(2)))(V-b)=RT`, answer the following questions:
At high pressure, the van der Waals equation gets reduced to
View SolutionCompressibility factor `Z=(PV)/(RT)`. Considering ideal gas, real gas, and gases at critical state, answer the following questions:
The cpmpressibility factor of an ideal gas is
View SolutionCompressibility factor `Z=(PV)/(RT)`. Considering ideal gas, real gas, and gases at critical state, answer the following questions:
The compressibility factor of a real gas is
View SolutionCompressibility factor `Z=(PV)/(RT)`. Considering ideal gas, real gas, and gases at critical state, answer the following questions:
The cpmpressibility factor of a gas is less than unity at `STP`, therefore
View SolutionCompressibility factor `Z=(PV)/(RT)`. Considering ideal gas, real gas, and gases at critical state, answer the following questions:
`Z_(c)` at `T_(c)`, `P_(c)`, and `V_(c)` is
View SolutionTwo gaseous molecules `A` and `B` are traveling towards each other. Let the mean free path of the molecule be `sigma` and `Z` be the collision number with other molecules at pressure `1 atm`. Answer the following questions
The free path of gas molecule is the distance
View SolutionTwo gaseous molecules `A` and `B` are traveling towards each other. Let the mean free path of the molecule be `sigma` and `Z` be the collision number with other molecules at pressure `1 atm`. Answer the following questions
If the mean free path is `sigma` at `1 atm` pressure, then its value at `5 atm` pressure is
View SolutionTwo gaseous molecules `A` and `B` are traveling towards each other. Let the mean free path of the molecule be `sigma` and `Z` be the collision number with other molecules at pressure `1 atm`. Answer the following questions
If `Z` is the total number of collisions which a gas molecule registers with others per unit time under particular conditions, then the collision frequency of the gas containing `N` molecules per unit volume is
View SolutionTwo gaseous molecules `A` and `B` are traveling towards each other. Let the mean free path of the molecule be `sigma` and `Z` be the collision number with other molecules at pressure `1 atm`. Answer the following questions
If the collision frequency of a gas at `1 atm` pressure is `Z`, then its collision frequency at `0.5 atm` is
View SolutionThe constant motion and high velocities of gas particles lead to some important practical consquences. One such consquences is that gases mix rapidly when they come in contact. Take the stopper off a bottle of perfume, for instance, and the odour will spread rapidly through the room as perfume molecules mix with the molecules in the air. This mixing of different gases by random molecular motion and with frequent collision is called diffusion. A similar process in which gas molecules escape without collision through a tiny hole into a vacuum is called effusion. Both the processes follow Graham's law which is mathematically put as `r prop sqrt(1//d)`. The average distance travelled by molecules between successive collisions is called mean free path.
Answer the following questions on the basis of the above information:
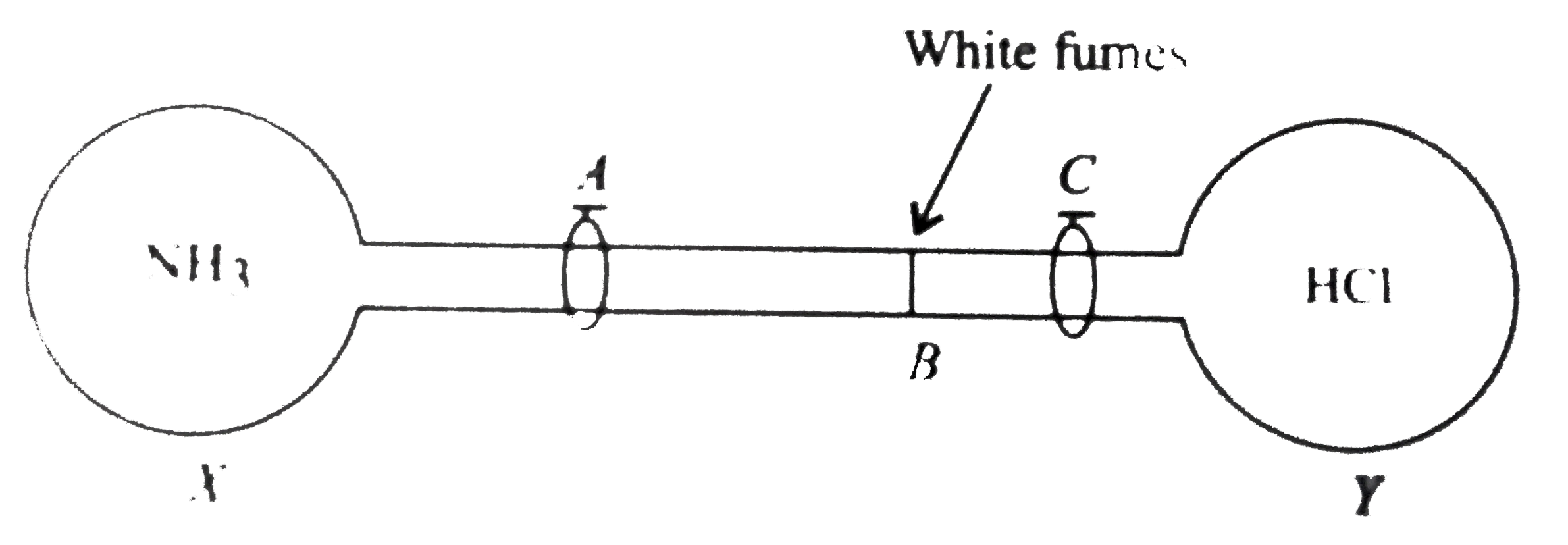
The stop cocks of the bulbs `X` (containing `NH_(3)`) and `Y` (containing `HCl`), both under indentical conditions, are opened simultaneously. White fumes of `NH_(4)Cl`, are formed at point `B`. If `AB=36.5 cm`, then `BC` is approximately
View SolutionThe constant motion and high velocities of gas particles lead to some important practical consquences. One such consquences is that gases mix rapidly when they come in contact. Take the stopper off a bottle of perfume, for instance, and the odour will spread rapidly through the room as perfume molecules mix with the molecules in the air. This mixing of different gases by random molecular motion and with frequent collision is called diffusion. A similar process in which gas molecules escape without collision through a tiny hole into a vacuum is called effusion. Both the processes follow Graham's law which is mathematically put as `r prop sqrt(1//d)`. The average distance travelled by molecules between successive collisions is called mean free path.
Answer the following questions on the basis of the above information:
Select the incorrect statement(s).
View SolutionThe constant motion and high velocities of gas particles lead to some important practical consquences. One such consquences is that gases mix rapidly when they come in contact. Take the stopper off a bottle of perfume, for instance, and the odour will spread rapidly through the room as perfume molecules mix with the molecules in the air. This mixing of different gases by random molecular motion and with frequent collision is called diffusion. A similar process in which gas molecules escape without collision through a tiny hole into a vacuum is called effusion. Both the processes follow Graham's law which is mathematically put as `r prop sqrt(1//d)`. The average distance travelled by molecules between successive collisions is called mean free path.
Answer the following questions on the basis of the above information:
Select the correct statement(s).
View SolutionThe constant motion and high velocities of gas particles lead to some important practical consquences. One such consquences is that gases mix rapidly when they come in contact. Take the stopper off a bottle of perfume, for instance, and the odour will spread rapidly through the room as perfume molecules mix with the molecules in the air. This mixing of different gases by random molecular motion and with frequent collision is called diffusion. A similar process in which gas molecules escape without collision through a tiny hole into a vacuum is called effusion. Both the processes follow Graham's law which is mathematically put as `r prop sqrt(1//d)`. The average distance travelled by molecules between successive collisions is called mean free path.
Answer the following questions on the basis of the above information:
`X mL H_(2)` effuses through a hole in a container in `5 s`. The time taken for the effusion of the same volume of the gas specified below under identical conditions is
View SolutionThe constant motion and high velocities of gas particles lead to some important practical consquences. One such consquences is that gases mix rapidly when they come in contact. Take the stopper off a bottle of perfume, for instance, and the odour will spread rapidly through the room as perfume molecules mix with the molecules in the air. This mixing of different gases by random molecular motion and with frequent collision is called diffusion. A similar process in which gas molecules escape without collision through a tiny hole into a vacuum is called effusion. Both the processes follow Graham's law which is mathematically put as `r prop sqrt(1//d)`. The average distance travelled by molecules between successive collisions is called mean free path.
Answer the following questions on the basis of the above information:
When `CO_(2)` under high pressure is released from a fire extinguisher, particles of solid `CO_(2)` are formed, despite the low sublimation temperature `(-77^(@)C)` at `1 atm` because
View SolutionThe behaviour of ideal gas is goverened by various gas laws which are described by mathematical statements as given below:
(`i`) `PV=k` (constant) at constant `n` and `T`
(`ii`) `V//T=k_(2)` (constant) at constant `n` and `P`
(`iii`) `V//n=k_(3)` (constant) at constant `T` and `P`
(`iv`) `PV=nRT`
(`v`) `P//T=k_(4) (constant) at constant `n` and `V`
Answer the following
The value of `k_(2)` is
View SolutionThe behaviour of ideal gas is goverened by various gas laws which are described by mathematical statements as given below:
(`i`) `PV=k` (constant) at constant `n` and `T`
(`ii`) `V//T=k_(2)` (constant) at constant `n` and `P`
(`iii`) `V//n=k_(3)` (constant) at constant `T` and `P`
(`iv`) `PV=nRT`
(`v`) `P//T=k_(4) (constant) at constant `n` and `V`
Answer the following
Avogadro's law is represented by the expression
View SolutionThe behaviour of ideal gas is goverened by various gas laws which are described by mathematical statements as given below:
(`i`) `PV=k` (constant) at constant `n` and `T`
(`ii`) `V//T=k_(2)` (constant) at constant `n` and `P`
(`iii`) `V//n=k_(3)` (constant) at constant `T` and `P`
(`iv`) `PV=nRT`
(`v`) `P//T=k_(4)` (constant) at constant `n` and `V`
Answer the following
A cylinder of `10 L` capacity at `300 K` containing the gas is used to fill balloons till finally the cylinder recorded a pressure of `10 m` bar. The number of `He` atoms still present in the cylinder is
View SolutionThe behaviour of ideal gas is goverened by various gas laws which are described by mathematical statements as given below:
(`i`) `PV=k` (constant) at constant `n` and `T`
(`ii`) `V//T=k_(2)` (constant) at constant `n` and `P`
(`iii`) `V//n=k_(3)` (constant) at constant `T` and `P`
(`iv`) `PV=nRT`
(`v`) `P//T=k_(4)` (constant) at constant `n` and `V`
Answer the following
The expression (`ii`) represents
View SolutionThe behaviour of ideal gas is goverened by various gas laws which are described by mathematical statements as given below:
(`i`) `PV=k` (constant) at constant `n` and `T`
(`ii`) `V//T=k_(2)` (constant) at constant `n` and `P`
(`iii`) `V//n=k_(3)` (constant) at constant `T` and `P`
(`iv`) `PV=nRT`
(`v`) `P//T=k_(4)` (constant) at constant `n` and `V`
Answer the following
If we plot a graph between volume (`L`) and temperature (`^(@)C`) by studying their variation for `2.0 g` of certain ideal gas at `1 bar` pressure, the graph obtained is a straight line which is
View SolutionConsider the adjacent diagram. Initially, flask `A` contained oxygen gas at `27^(@)C` and `950 mm` of `Hg`, and flask `B` contained neon gas at `27^(@)C` and `900 mm`. Finally, two flask were joined by means of a narrow tube of negligible volume equipped with a stopcock and gases were allowed to mixup freely. The final pressure in the combined system was found to be `910 mm` of `Hg`.

Which of the following statements concerning oxygen and neon gas is true in the begining, when the stopcock was just opened?
View SolutionConsider the adjacent diagram. Initially, flask `A` contained oxygen gas at `27^(@)C` and `950 mm` of `Hg`, and flask `B` contained neon gas at `27^(@)C` and `900 mm`. Finally, two flask were joined by means of a narrow tube of negligible volume equipped with a stopcock and gases were allowed to mixup freely. The final pressure in the combined system was found to be `910 mm` of `Hg`.

What is the correct relationship between volumes of the two flasks?
View SolutionConsider the adjacent diagram. Initially, flask `A` contained oxygen gas at `27^(@)C` and `950 mm` of `Hg`, and flask `B` contained neon gas at `27^(@)C` and `900 mm`. Finally, two flask were joined by means of a narrow tube of negligible volume equipped with a stopcock and gases were allowed to mixup freely. The final pressure in the combined system was found to be `910 mm` of `Hg`.

If flask `B` were heated to `127^(@)C`, maintaining flask `A` at constant temperature of `27^(@)C`, final pressure (in `mm Hg`) in the combined system would have been
View SolutionThe system shown in the figure is in equilibrium, where `A` and `B` are isomeric liquids and form an ideal solution at `TK`. Standard vapour pressures of `A` and `B` are `P_(A)^(0)` and `P_(B)^(0)`, respectively, at `TK`. We collect the vapour of `A` and `B` in two containers of volume `V`, first container is maintained at `2 T K` and second container is maintained at `3T//2`. At the temperature greater than `T K`, both `A` and `B` exist in only gaseous form.
We assume than collected gases behave ideally at `2 T K` and there may take place an isomerisation reaction in which `A` gets converted into `B` by first-order kinetics reaction given as:
`Aoverset(k)rarrB`, where `k` is a rate constant.
In container (`II`) at the given temperature `3T//2`, `A` and `B` are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

`r=K.(P)/(sqrt(M_(0)))`
where `P=` pressure differences between system and surrounding
`K=` positive constant
`M_(0)=` molecular weight of the gas
If partial vapour pressure of `A` is twice that of partial vapour pressure of `B` and total vapour pressure `2` atm at `T K`, where `T=50 K` and `V=8.21 L`, then the number of moles of `A` and `B` in vapour phase is:
View SolutionThe system shown in the figure is in equilibrium, where `A` and `B` are isomeric liquids and form an ideal solution at `TK`. Standard vapour pressures of `A` and `B` are `P_(A)^(0)` and `P_(B)^(0)`, respectively, at `TK`. We collect the vapour of `A` and `B` in two containers of volume `V`, first container is maintained at `2 T K` and second container is maintained at `3T//2`. At the temperature greater than `T K`, both `A` and `B` exist in only gaseous form.
We assume than collected gases behave ideally at `2 T K` and there may take place an isomerisation reaction in which `A` gets converted into `B` by first-order kinetics reaction given as:
`Aoverset(k)rarrB`, where `k` is a rate constant.
In container (`II`) at the given temperature `3T//2`, `A` and `B` are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

`r=K.(P)/(sqrt(M_(0)))`
where `P=` pressure differences between system and surrounding
`K=` positive constant
`M_(0)=` molecular weight of the gas
Vapours of `A` and `B` are passed into a container of volume `8.21 L`, maintained at `2T K`, where `T=50 K` and after `5 min`, moles of `B=8//3`. The pressure developed into the cotainer after two half lives is
View SolutionThe system shown in the figure is in equilibrium, where `A` and `B` are isomeric liquids and form an ideal solution at `TK`. Standard vapour pressures of `A` and `B` are `P_(A)^(0)` and `P_(B)^(0)`, respectively, at `TK`. We collect the vapour of `A` and `B` in two containers of volume `V`, first container is maintained at `2 T K` and second container is maintained at `3T//2`. At the temperature greater than `T K`, both `A` and `B` exist in only gaseous form.
We assume than collected gases behave ideally at `2 T K` and there may take place an isomerisation reaction in which `A` gets converted into `B` by first-order kinetics reaction given as:
`Aoverset(k)rarrB`, where `k` is a rate constant.
In container (`II`) at the given temperature `3T//2`, `A` and `B` are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

`r=K.(P)/(sqrt(M_(0)))`
where `P=` pressure differences between system and surrounding
`K=` positive constant
`M_(0)=` molecular weight of the gas
If vapours are collected in a container of volume `8.21 L` maintained at `3 T//2K`, where `T=50 K`, then the ratio of initial rate of effusion of gases `A` and `B` is given as
View Solution
Exercises (Linked Comprehensive) questions and complete solutions for chapter STATES OF MATTER of CENGAGE CHEMISTRY (HINGLISH) of Class 11
All Exercises from CENGAGE CHEMISTRY Class 11 CHEMISTRY STATES OF MATTER
- Archives ( Assertion-Reasoning)
- Archives (Integer)
- Archives (Multiple Correct)
- Archives (Single Correct)
- Archives (Subjective)
- Ex 5.1
- Ex 5.2
- Ex 5.3
- Ex 5.4
- Exercises
- Exercises (Assertion-Reasoning)
- Exercises (Fill In The Blanks)
- Exercises (Integer)
- Exercises (Linked Comprehensive)
- Exercises (Multiple Correcttype)
- Exercises (Single Correct)
- Exercises (Ture False)
- Solved Example