Complete Solutions to Exercises (Linked Comprehension) of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| CENGAGE CHEMISTRY | Exercises (Linked Comprehension) |
| Number Of Questions | 74 |
| Academic Year | 2023-24 |
Gibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
`(DeltaG)_(PT) = DeltaH - T DeltaS`
The magnitude of `DeltaH` does not change much with the change in temperature but the enrgy factor `T DeltaS` changes appreciably. Thus, spontaneity of a process depends very much on temperature.
When `CaCO_(3)` is heated to a high temperature, it undergoes decomposition into `CaO` and `CO_(2)` whereas it is quite stable at room temperature. The most likely explanation of its is
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
`(DeltaG)_(PT) = DeltaH - T DeltaS`
The magnitude of `DeltaH` does not change much with the change in temperature but the enrgy factor `T DeltaS` changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For the reaction at `25^(2)C, X_(2)O_(4)(l) rarr 2XO_(2)`
`DeltaH = 2.0 kcal `and `DeltaS = 20 cal K^(-1)`. the reaction would be
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
`(DeltaG)_(PT) = DeltaH - T DeltaS`
The magnitude of `DeltaH` does not change much with the change in temperature but the enrgy factor `T DeltaS` changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For the reaction at `298K, 2A +B rarr C`
`Deltah = 100 kcal` and `DeltaS = 0.020 kcla K^(-1)`. If `DeltaH` and `DeltaS` are assumed to be constant over the temperature range, at what temperature will the reaction become spontaneous?
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
`(DeltaG)_(PT) = DeltaH - T DeltaS`
The magnitude of `DeltaH` does not change much with the change in temperature but the enrgy factor `T DeltaS` changes appreciably. Thus, spontaneity of a process depends very much on temperature.
A reaction has value of `DeltaH - 20 kcal` at `200K` , the reaction is spontaneous, below this temperature, it is not. the values `DeltaG` and `DeltaS` at `400K` are, respectively
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
`(DeltaG)_(PT) = DeltaH - T DeltaS`
The magnitude of `DeltaH` does not change much with the change in temperature but the enrgy factor `T DeltaS` changes appreciably. Thus, spontaneity of a process depends very much on temperature.
The enthalpy change for a certain reaction at `300K` is `-15.0 kcal mol^(-1)`. The entropy change under these conditions is `-7.2 cal K^(-) mol^(-1)`. The free enegry change for the reaction and its spontaneous//nonspontaneous character will be
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
`(DeltaG)_(PT) = DeltaH - T DeltaS`
The magnitude of `DeltaH` does not change much with the change in temperature but the enrgy factor `T DeltaS` changes appreciably. Thus, spontaneity of a process depends very much on temperature.
The dissolution of `CaCI_(2).6H_(2)O` in a large volume of water is endothermic to the extent of `3.5 kcal mol^(-1)`. For the reaction. `CaCI_(2)(s) +6H_(2)O(l) rarrCaCI_(2).6H_(2)O(s) DeltaH is -23.2 kcal`. The heat of solution of anhydrous `CaCI_(2)` in large quantity of water will be
View SolutionGiven that `,`
`A(s) rarr A(l)DeltaH=x`
`A(l) rarr A(g), DeltaH=y`
The heat of sublimation of `A` will be `:`
View SolutionThe enthalpy change for chemical reaction is denoted aas `DeltaH^(Theta)` and `DeltaH^(Theta) = H_(P)^(Theta) - H_(R)^(Theta)`. The relation between enthalpy and internal enegry is expressed by equation:
`DeltaH = DeltaU +DeltanRT`
where `DeltaU =` change in internal enegry `Deltan =` change in number of moles, `R =` gas constant.
`H_(2)(g) +((1)/(2))O_(2)(g) = H_(2)O(l), DeltaH_(298K) = - 68.00kcal`
Heat of voporisation of water at `1` atm and `25^(@)C` is `10.00 kcal`. The standard heat of formation (in kcal) of `1` amol vapour a `25^(@)C` is
View SolutionThe enthalpy change for chemical reaction is denoted as `DeltaH^(Theta)` and `DeltaH^(Theta) = H_(P)^(Theta) - H_(R)^(Theta)`. The relation between enthalpy and internal enegry is expressed by equation:
`DeltaH = DeltaU +DeltanRT`
where `DeltaU =` change in internal enegry `Deltan =` change in number of moles, `R =` gas constant.
For the change, `C_("diamond") rarr C_("graphite"), DeltaH =- 1.89 kJ`, if `6g` of diamond and `6g` of graphite are seperately burnt to yield `CO_(2)` the heat liberated in first case is
View SolutionThe enthalpy change for chemical reaction is denoted aas `DeltaH^(Theta)` and `DeltaH^(Theta) = H_(P)^(Theta) - H_(R)^(Theta)`. The relation between enthalpy and internal enegry is expressed by equation:
`DeltaH = DeltaU +DeltanRT`
where `DeltaU =` change in internal enegry `Deltan =` change in number of moles, `R =` gas constant.
Which of the following equations corresponds to the definition of enthalpy of formation at `298K`?
View SolutionThe enthalpy change for chemical reaction is denoted aas `DeltaH^(Theta)` and `DeltaH^(Theta) = H_(P)^(Theta) - H_(R)^(Theta)`. The relation between enthalpy and internal enegry is expressed by equation:
`DeltaH = DeltaU +DeltanRT`
where `DeltaU =` change in internal enegry `Deltan =` change in number of moles, `R =` gas constant.
Enthalpy of the system is given as
View SolutionThe enthalpy change for chemical reaction is denoted aas `DeltaH^(Theta)` and `DeltaH^(Theta) = H_(P)^(Theta) - H_(R)^(Theta)`. The relation between enthalpy and internal enegry is expressed by equation:
`DeltaH = DeltaU +DeltanRT`
where `DeltaU =` change in internal enegry `Deltan =` change in number of moles, `R =` gas constant.
For a reaction, `2X(s) +2Y(s) rarr 2C(l) +D(g), DeltaH` at `27^(@)C` is `-28 kcal mol^(-1). DeltaU` is .....`kcal mol^(-1)`
View SolutionFor an ideal gas, an illustratio of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.
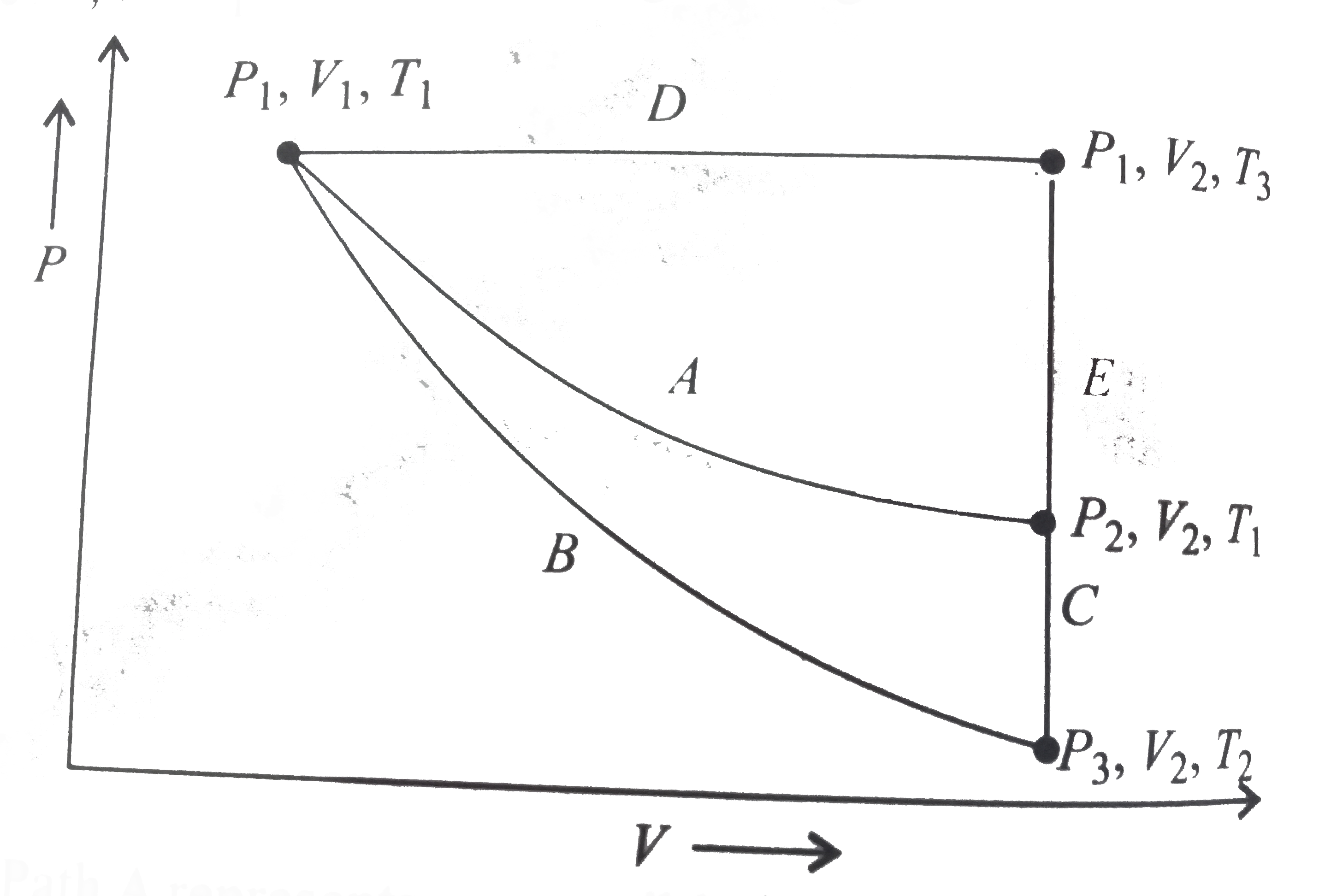
Path `A`represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `q_(rev)`, for path `(A)`?
View SolutionFor an ideal gas, an illustratio of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.

Path `A`represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `q_(rev)`, for path `(B +C)`?
View SolutionFor an ideal gas, an illustratio of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.

Path `A`represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `DeltaS` for path `A`?
View SolutionFor an ideal gas, an illustratio of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.
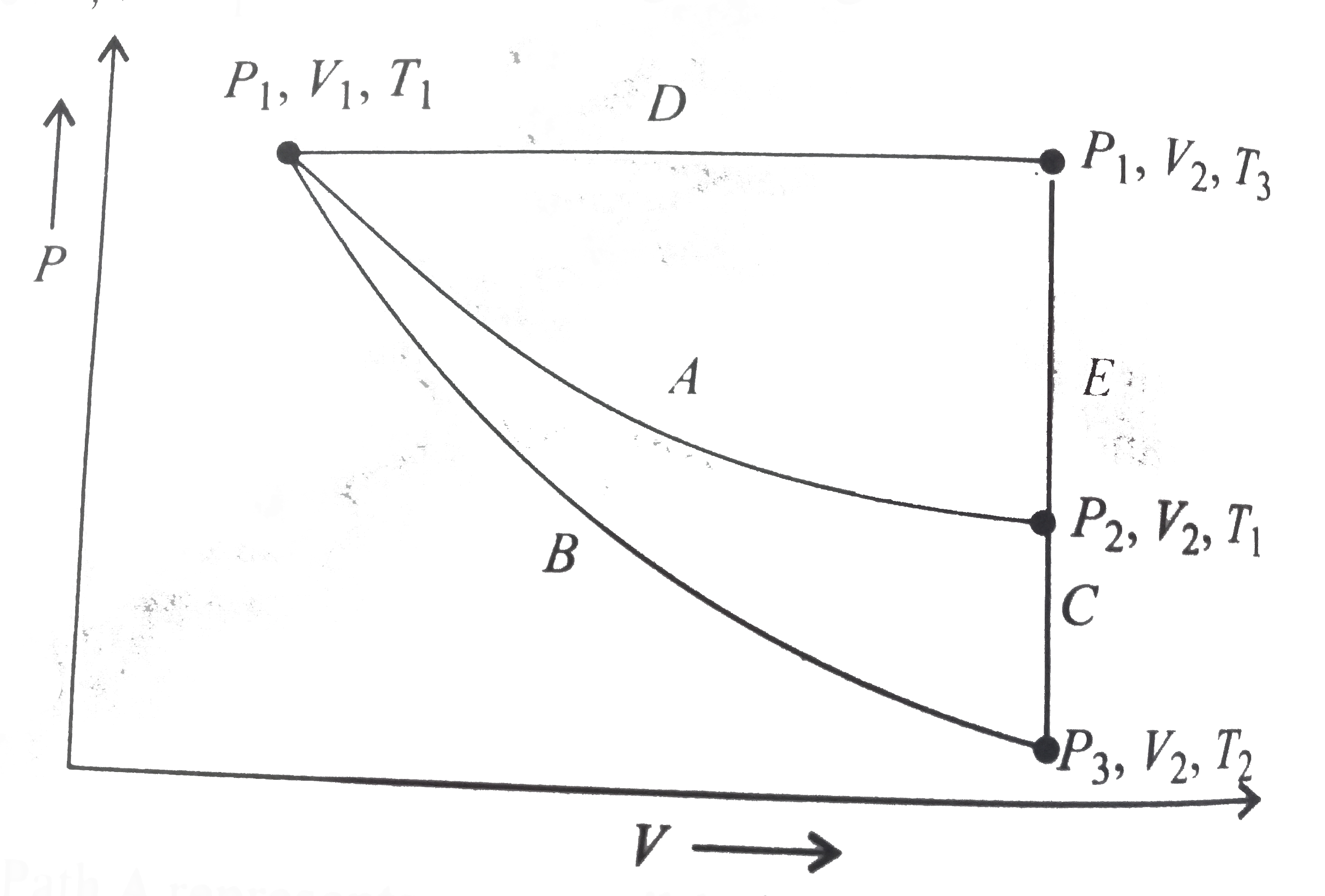
Path `A`represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `q_(rev)`, for path `(D+E)`?
View SolutionFor an ideal gas, an illustratio of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.
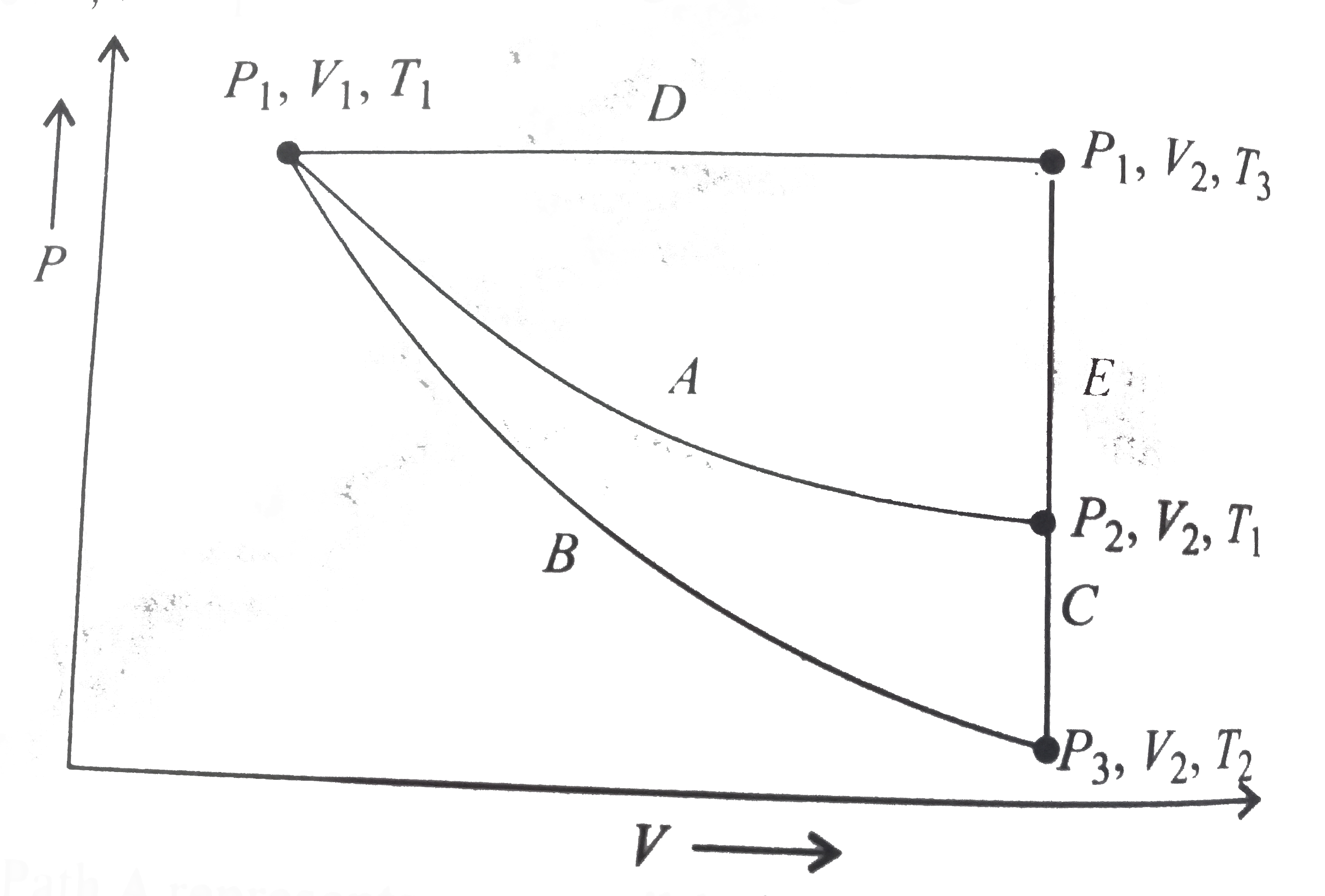
Path `A`represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `DeltaS` for path `(D +E)`?
View SolutionConcrete is produced form a mixture of cement, water and small stones. Small amount of gypsum, `CaSO_(4).2H_(2)O` is added in coment production to impove the subsequent hardening of concrete. The elevated temperature during the production of cement may lead to the formation of unwanted hemihydrate `CaSO_(4)(1)/(2)H_(2)O` according to reaction.
`CaSO_(4)2H_(2)O(s) rarr CaSO_(4)(1)/(2)H_(2)O(s)+(3)/(2)H_(2)O(g)`
The `Delta_(f)H^(Theta) of CaSO_(2).2H_(2)O(s),CaSO_(4)(1)/(2)H_(2)O(s),H_(2)O(g)`
are `-2021.0 kJ mol^(-1), -1575.0 kJ mol^(-1)` and `-241.8 kJ mol^(-1)`, respectively. The respective values of their standard entropies are `194.0, 130.0` and `188.0 J K^(-1)mol^(-1)`. The values of `R = 8.314JK^(-1)mol^(-1) = 0.0831L` bar `mol^(-1)K^(-1)`.
Answer the following questions on the basis of above information.
Heat change occuring during conservation of `1kg` of `CaSO_(4).2H_(2)O(s)` (molar mass `172g mol^(-1))` of `CaSO_(4)(1)/(2)H_(2)O(s)` is equal to
View SolutionConcrete is produced form a mixture of cement, water and small stones. Small amount of gypsum, `CaSO_(4).2H_(2)O` is added in coment production to impove the subsequent hardening of concrete. The elevated temperature during the production of cement may lead to the formation of unwanted hemihydrate `CaSO_(4)(1)/(2)H_(2)O` according to reaction.
`CaSO_(4)2H_(2)O(s) rarr CaSO_(4)(1)/(2)H_(2)O(s)+(3)/(2)H_(2)O(g)`
The `Delta_(f)H^(Theta) of CaSO_(2).2H_(2)O(s),CaSO_(4)(1)/(2)H_(2)O(s),H_(2)O(g)`
are `-2021.0 kJ mol^(-1), -1575.0 kJ mol^(-1)` and `-241.8 kJ mol^(-1)`, respectively. The respective values of their standard entropies are `194.0, 130.0` and `188.0 J K^(-1)mol^(-1)`. The values of `R = 8.314JK^(-1)mol^(-1) = 0.0831L` bar `mol^(-1)K^(-1)`.
Answer the following questions on the basis of above information.
The value of `DeltaG^(Theta)` for the reaction at `298K` is
View SolutionConcrete is produced form a mixture of cement, water and small stones. Small amount of gypsum, `CaSO_(4).2H_(2)O` is added in coment production to impove the subsequent hardening of concrete. The elevated temperature during the production of cement may lead to the formation of unwanted hemihydrate `CaSO_(4)(1)/(2)H_(2)O` according to reaction.
`CaSO_(4)2H_(2)O(s) rarr CaSO_(4)(1)/(2)H_(2)O(s)+(3)/(2)H_(2)O(g)`
The `Delta_(f)H^(Theta) of CaSO_(2).2H_(2)O(s),CaSO_(4)(1)/(2)H_(2)O(s),H_(2)O(g)`
are `-2021.0 kJ mol^(-1), -1575.0 kJ mol^(-1)` and `-241.8 kJ mol^(-1)`, respectively. The respective values of their standard entropies are `194.0, 130.0` and `188.0 J K^(-1)mol^(-1)`. The values of `R = 8.314JK^(-1)mol^(-1) = 0.0831L` bar`mol^(-1)K^(-1)`.
Answer the following questions on the basis of above information.
The value of equilibrium for reaction is
View SolutionConcrete is produced form a mixture of cement, water and small stones. Small amount of gypsum, `CaSO_(4).2H_(2)O` is added in coment production to impove the subsequent hardening of concrete. The elevated temperature during the production of cement may lead to the formation of unwanted hemihydrate `CaSO_(4)(1)/(2)H_(2)O` according to reaction.
`CaSO_(4)2H_(2)O(s) rarr CaSO_(4)(1)/(2)H_(2)O(s)+(3)/(2)H_(2)O(g)`
The `Delta_(f)H^(Theta) of CaSO_(2).2H_(2)O(s),CaSO_(4)(1)/(2)H_(2)O(s),H_(2)O(g)`
are `-2021.0 kJ mol^(-1), -1575.0 kJ mol^(-1)` and `-241.8 kJ mol^(-1)`, respectively. The respective values of their standard entropies are `194.0, 130.0` and `188.0 J K^(-1)mol^(-1)`. The values of `R = 8.314JK^(-1)mol^(-1) = 0.0831L` bar `mol^(-1)K^(-1)`.
Answer the following questions on the basis of above information.
The equilibrium pressure of water vapour in closed vessel containing `CaSO_(4)2H_(2)O(s),CaSO_(4)(1)/(2)H_(2)O(s)` and `H_(2)O(g)` at `298K` (Antilog `-3.14 = 7.24 xx 10^(-4))` is
View SolutionConcrete is produced form a mixture of cement, water and small stones. Small amount of gypsum, `CaSO_(4).2H_(2)O` is added in coment production to impove the subsequent hardening of concrete. The elevated temperature during the production of cement may lead to the formation of unwanted hemihydrate `CaSO_(4)(1)/(2)H_(2)O` according to reaction.
`CaSO_(4)2H_(2)O(s) rarr CaSO_(4)(1)/(2)H_(2)O(s)+(3)/(2)H_(2)O(g)`
The `Delta_(f)H^(Theta) of CaSO_(2).2H_(2)O(s),CaSO_(4)(1)/(2)H_(2)O(s),H_(2)O(g)`
are `-2021.0 kJ mol^(-1), -1575.0 kJ mol^(-1)` and `-241.8 kJ mol^(-1)`, respectively. The respective values of their standard entropies are `194.0, 130.0` and `188.0 J K^(-1)mol^(-1)`. The values of `R = 8.314JK^(-1)mol^(-1) = 0.0831L` bar `mol^(-1)K^(-1)`.
Answer the following questions on the basis of above information.
The formation of `CaSO_(4)(1)/(2)H_(2)O`at `298K` is
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume `V_(1)` to volume `V_(2)`. The initial pressure is `P_(1)` and the final pressure is `P_(2)`. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume `V_(1) to V_(2)`. The initial pressure being same but final pressure is `P_(2)`.
The work of expansion in adiabatic process `(w_(adi))` is related to work of expansion in isothermal process `(w_(iso))` is
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume `V_(1)` to volume `V_(2)`. The initial pressure is `P_(1)` and the final pressure is `P_(2)`. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume `V_(1) to V_(2)`. The initial pressure being same but final pressure is `P_(2)`.
Which of the following is correct?
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume `V_(1)` to volume `V_(2)`. The initial pressure is `P_(1)` and the final pressure is `P_(2)`. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume `V_(1) to V_(2)`. The initial pressure being same but final pressure is `P_(2)`.
Which graphic representation is correct
a.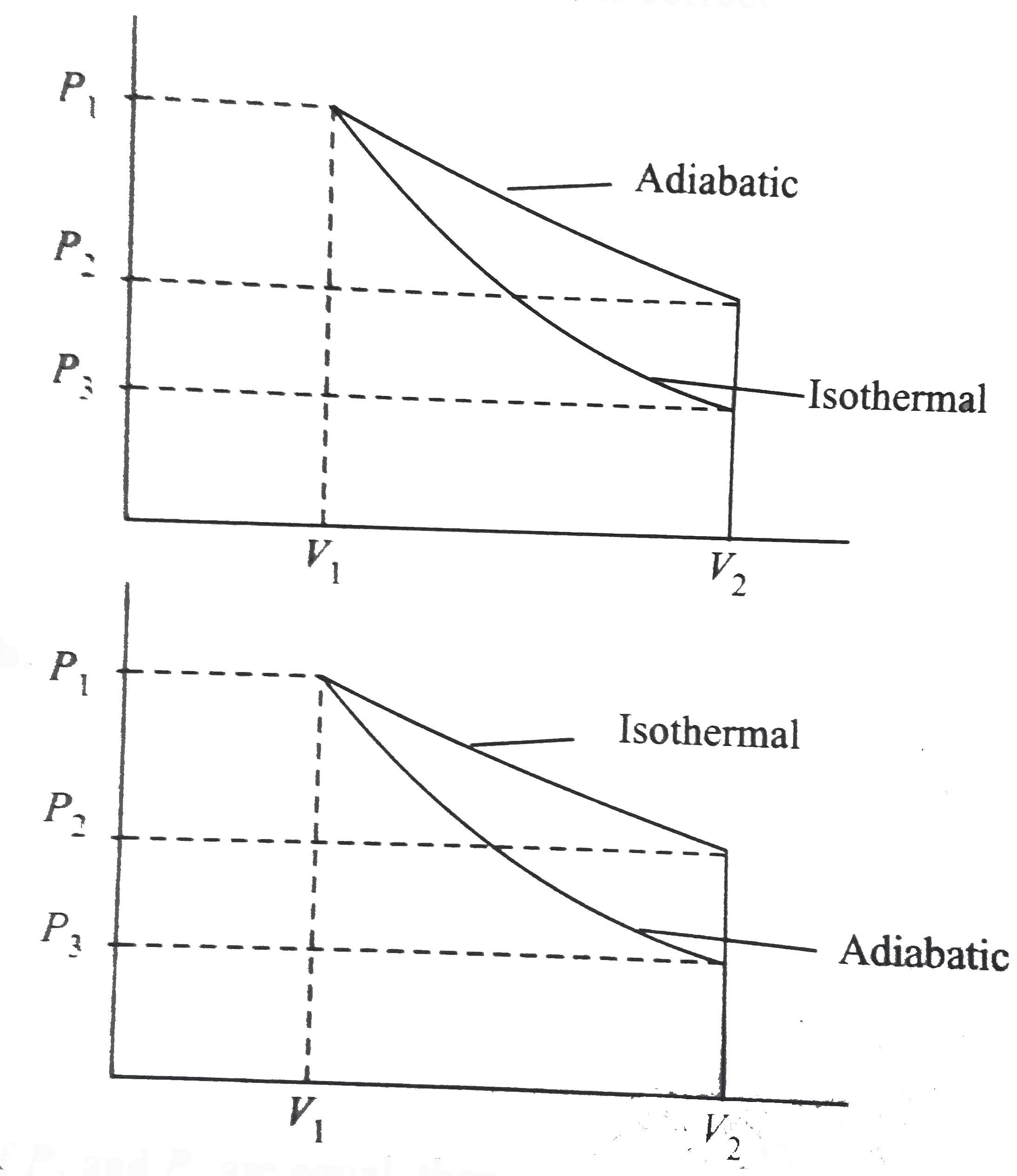
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume `V_(1)` to volume `V_(2)`. The initial pressure is `P_(1)` and the final pressure is `P_(2)`. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume `V_(1) to V_(2)`. The initial pressure being same but final pressure is `P_(2)`.
If `P_(3)` and `P_(2)` are equal, then
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume `V_(1)` to volume `V_(2)`. The initial pressure is `P_(1)` and the final pressure is `P_(2)`. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume `V_(1) to V_(2)`. The initial pressure being same but final pressure is `P_(2)`.
Which relation is correct `(gamma = (C_(P))/(C_(V)))`?
View SolutionFree enegry , `G = H - TS`, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of `TS` as the part of the system's enegry that is disordered already, then `(H -TS)` is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, `DeltaG = DeltaH - T DeltaS` From the second law of thermodynamics, a reaction is spontaneous if `Delta_("total")S` is positive, non-spontaneous if `Delta_("total")S` is negative, and at equilibrium if `Delta_('total")S` is zero.
Since, `-T DeltaS = DeltaG` and since `DeltaG` and `DeltaS` have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF `DeltaG lt 0`, the reaction is spontaneous.
If `DeltaG gt 0`, the reaction is non-spontaneous.
If `DeltaG = 0`, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
For the spontaneity of a reaction, which statement is true?
View SolutionFree enegry , `G = H - TS`, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of `TS` as the part of the system's enegry that is disordered already, then `(H -TS)` is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, `DeltaG = DeltaH - T DeltaS` From the second law of thermodynamics, a reaction is spontaneous if `Delta_("total")S` is positive, non-spontaneous if `Delta_("total")S` is negative, and at equilibrium if `Delta_('total")S` is zero.
Since, `-T DeltaS = DeltaG` and since `DeltaG` and `DeltaS` have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF `DeltaG lt 0`, the reaction is spontaneous.
If `DeltaG gt 0`, the reaction is non-spontaneous.
If `DeltaG = 0`, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
A particular reaction has a negative value for the free energy change. Then at ordinary temperature
View SolutionFree enegry , `G = H - TS`, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of `TS` as the part of the system's enegry that is disordered already, then `(H -TS)` is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, `DeltaG = DeltaH - T DeltaS` From the second law of thermodynamics, a reaction is spontaneous if `Delta_("total")S` is positive, non-spontaneous if `Delta_("total")S` is negative, and at equilibrium if `Delta_('total")S` is zero.
Since, `-T DeltaS = DeltaG` and since `DeltaG` and `DeltaS` have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF `DeltaG lt 0`, the reaction is spontaneous.
If `DeltaG gt 0`, the reaction is non-spontaneous.
If `DeltaG = 0`, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
Which of the following is true for the reaction?
`H_(2)O(l) hArr H_(2)O(g) at 100^(@)C` and `1` atmosphere
View SolutionFree enegry , `G = H - TS`, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of `TS` as the part of the system's enegry that is disordered already, then `(H -TS)` is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, `DeltaG = DeltaH - T DeltaS` From the second law of thermodynamics, a reaction is spontaneous if `Delta_("total")S` is positive, non-spontaneous if `Delta_("total")S` is negative, and at equilibrium if `Delta_('total")S` is zero.
Since, `-T DeltaS = DeltaG` and since `DeltaG` and `DeltaS` have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF `DeltaG lt 0`, the reaction is spontaneous.
If `DeltaG gt 0`, the reaction is non-spontaneous.
If `DeltaG = 0`, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
If an endothermic reaction is non-spontaneous at freezing point of water and becomes feasible at its boiling point, then
View SolutionFree enegry , `G = H - TS`, is state function that indicates whther a reaction is spontaneous or non-spontaneous. If you think of `TS` as the part of the system's enegry that is disordered already, then `(H -TS)` is the part of the system's energy that is still ordered and therefore free to cause spontaneous change by becoming disordered.
Also, `DeltaG = DeltaH - T DeltaS` From the second law of thermodynamics, a reaction is spontaneous if `Delta_("total")S` is positive, non-spontaneous if `Delta_("total")S` is negative, and at equilibrium if `Delta_('total")S` is zero.
Since, `-T DeltaS = DeltaG` and since `DeltaG` and `DeltaS` have opposite sings, we can restate the thermodynamic criterion for the spontaneity of a reaction carried out a constant temperature and pressure.
IF `DeltaG lt 0`, the reaction is spontaneous.
If `DeltaG gt 0`, the reaction is non-spontaneous.
If `DeltaG = 0`, the reaction is at equilibrium.
Read the above paragraph carefully and answer the following questions based on the above comprehension.
One mole of ice si converted to liquid at `273 K, H_(2)O(s)` and `H_(2)O(l)` have entropies `38.20` and `60.03 J mol^(-1) dg^(-1)`. Enthalpy change in the conversion will be
View SolutionThe state of a mole of an ideal gas changed from state `A` at pressure `2P` and volume `V` follows four different processes and finally returns to initial state `A` reversibly as shown below in the graph. By interpreting the graph, answer the following questions.

Which is the kind of process followed from state `A` to state, `B`?
View SolutionThe state of a mole of an ideal gas changed from state `A` at pressure `2P` and volume `V` follows four different processes and finally returns to initial state `A` reversibly as shown below in the graph. By interpreting the graph, answer the following questions.

In state `D` to state `A`, what kind of process is followed?
View SolutionThe state of a mole of an ideal gas changed from state `A` at pressure `2P` and volume `V` follows four different processes and finally returns to initial state `A` reversibly as shown below in the graph. By interpreting the graph, answer the following questions.
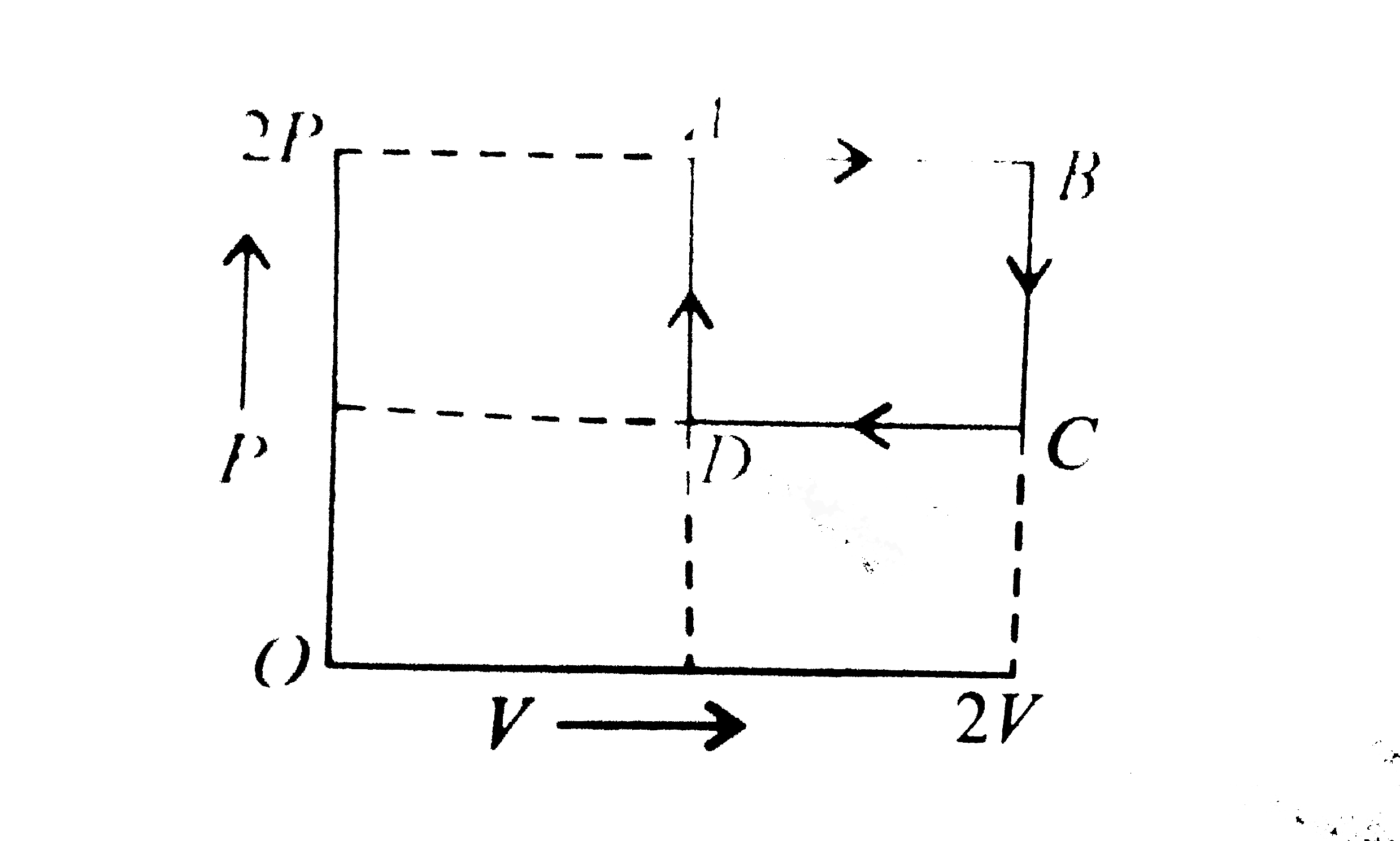
what would the be total done by the gas?
View SolutionThe state of a mole of an ideal gas changed from state `A` at pressure `2P` and volume `V` follows four different processes and finally returns to initial state `A` reversibly as shown below in the graph. By interpreting the graph, answer the following questions.
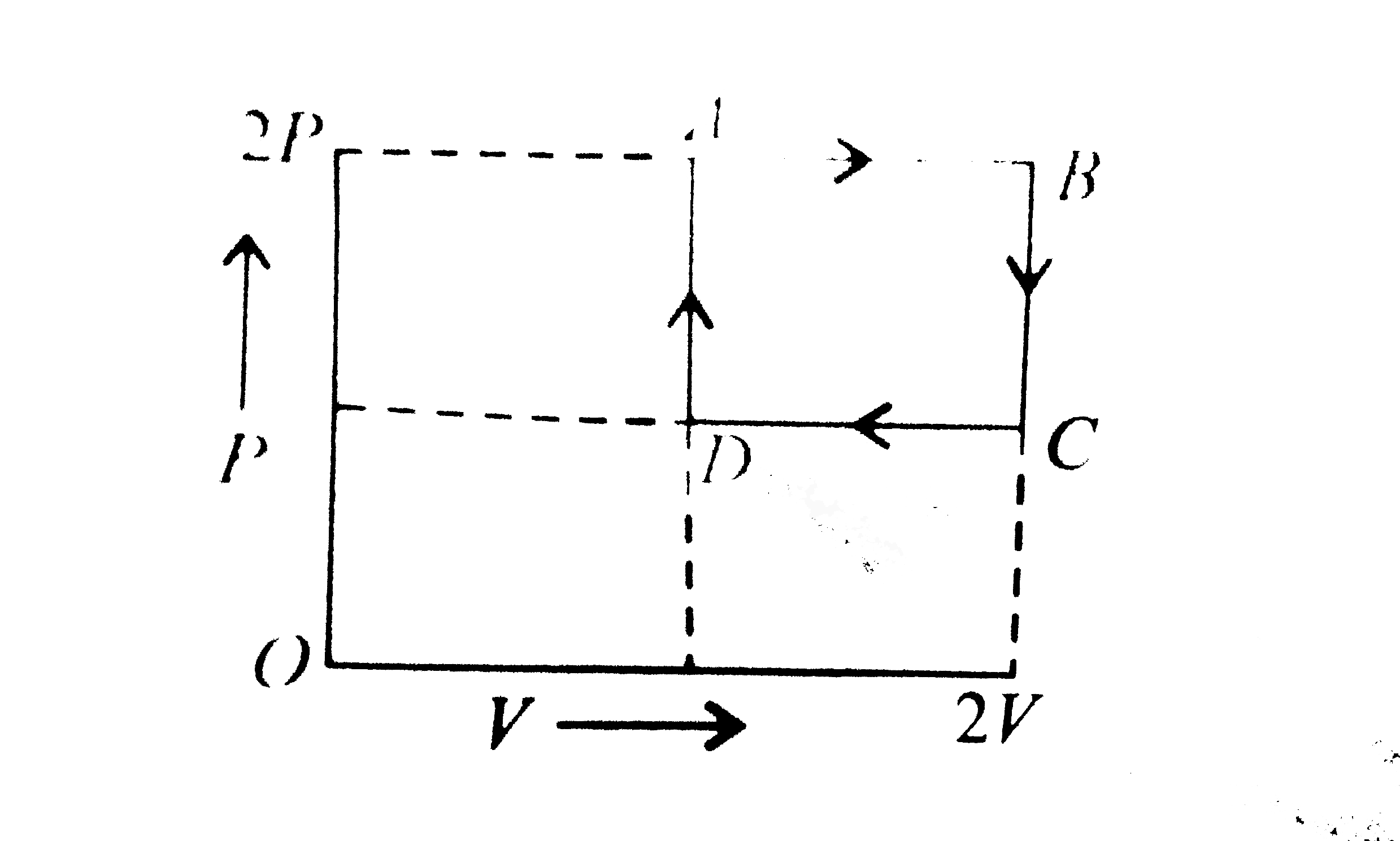
What would be the work done in state `B to C`?
View SolutionThe state of a mole of an ideal gas changed from state `A` at pressure `2P` and volume `V` follows four different processes and finally returns to initial state `A` reversibly as shown below in the graph. By interpreting the graph, answer the following questions.
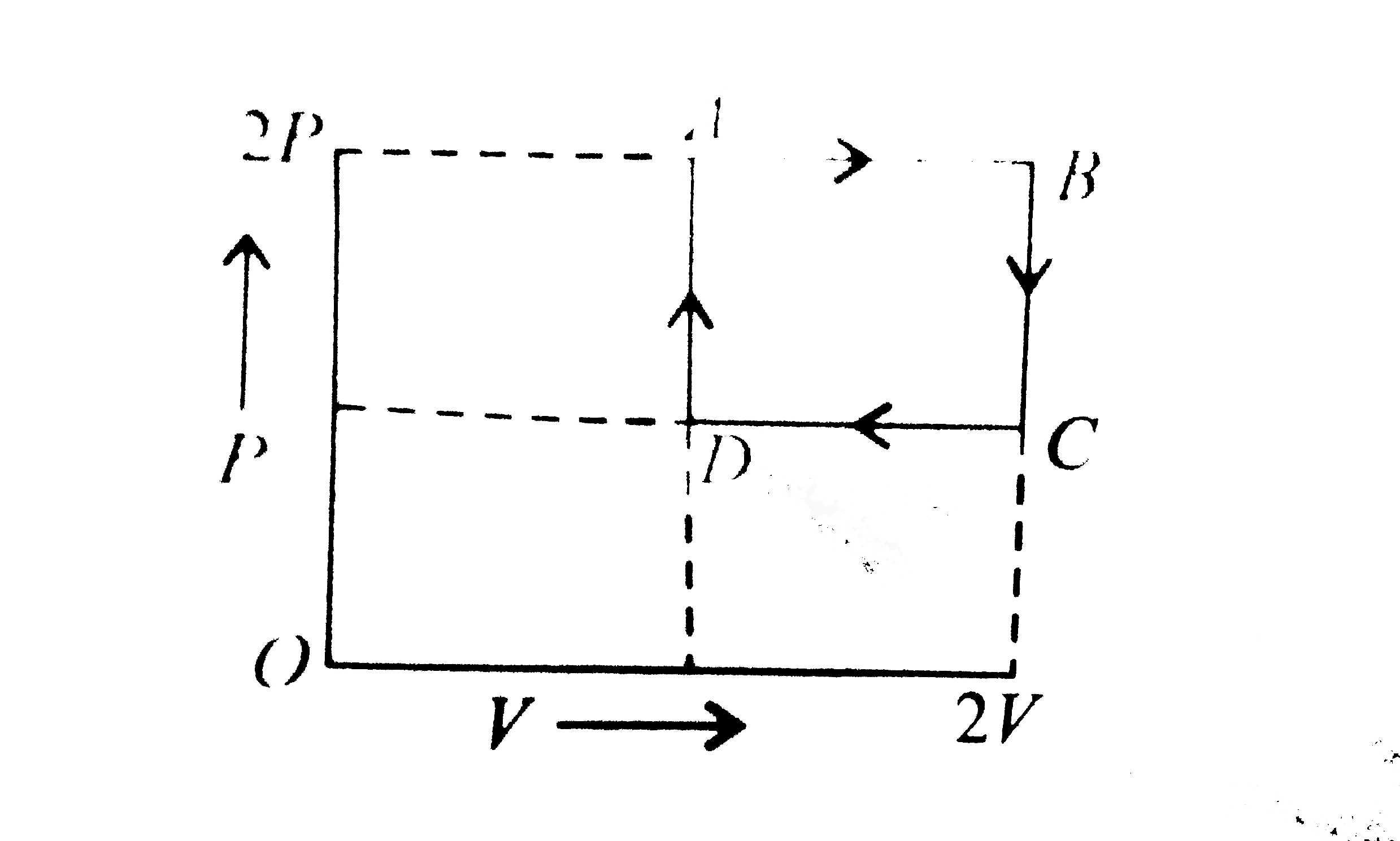
What would be the heat obsorbed by the system in this cyclic process?
View SolutionThe second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of `CO_(2)` gas expands isothermally (in thermal contact with the surroundings, temperature `= 15.0^(@)C`) against a fixed external pressure of `1.00 bar`. The initial and final volumes of the gas are `10.0 L` and `30.0L`, respectively.
Select the correct order of the entropy change.
View SolutionThe second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of `CO_(2)` gas expands isothermally (in thermal contact with the surroundings, temperature `= 15.0^(@)C`) against a fixed external pressure of `1.00 bar`. The initial and final volumes of the gas are `10.0 L` and `30.0L`, respectively.
Assuming `CO_(2)` to be an ideal gas, `Delta_(sys)S` is
View SolutionThe second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of `CO_(2)` gas expands isothermally (in thermal contact with the surroundings, temperature `= 15.0^(@)C`) against a fixed external pressure of `1.00` bar. The initial and final volumes of the gas are `10.0 L` and `30.0L`, respectively.
`Delta_(surr)S` is
View SolutionA sample consisting of `1mol` of a mono-atomic perfect gas `(C_(V) = (3)/(2)R)` is taken through the cycle as shown.
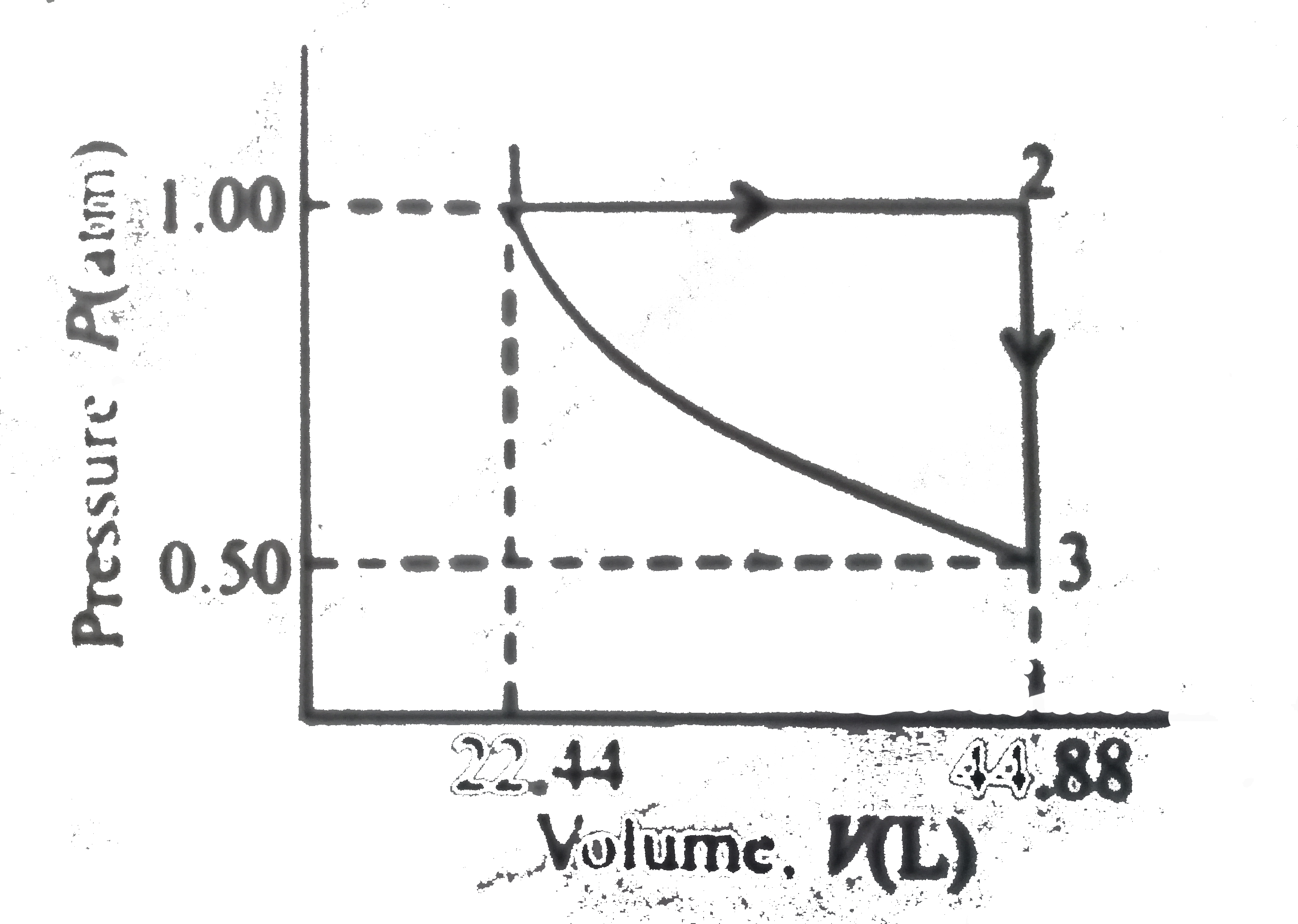
Temperature at points `(1),(2)` and `(3)` respectively is
View SolutionA sample consisting of `1mol` of a mono-atomic perfect gas `(C_(V) = (3)/(2)R)` is taken through the cycle as shown.
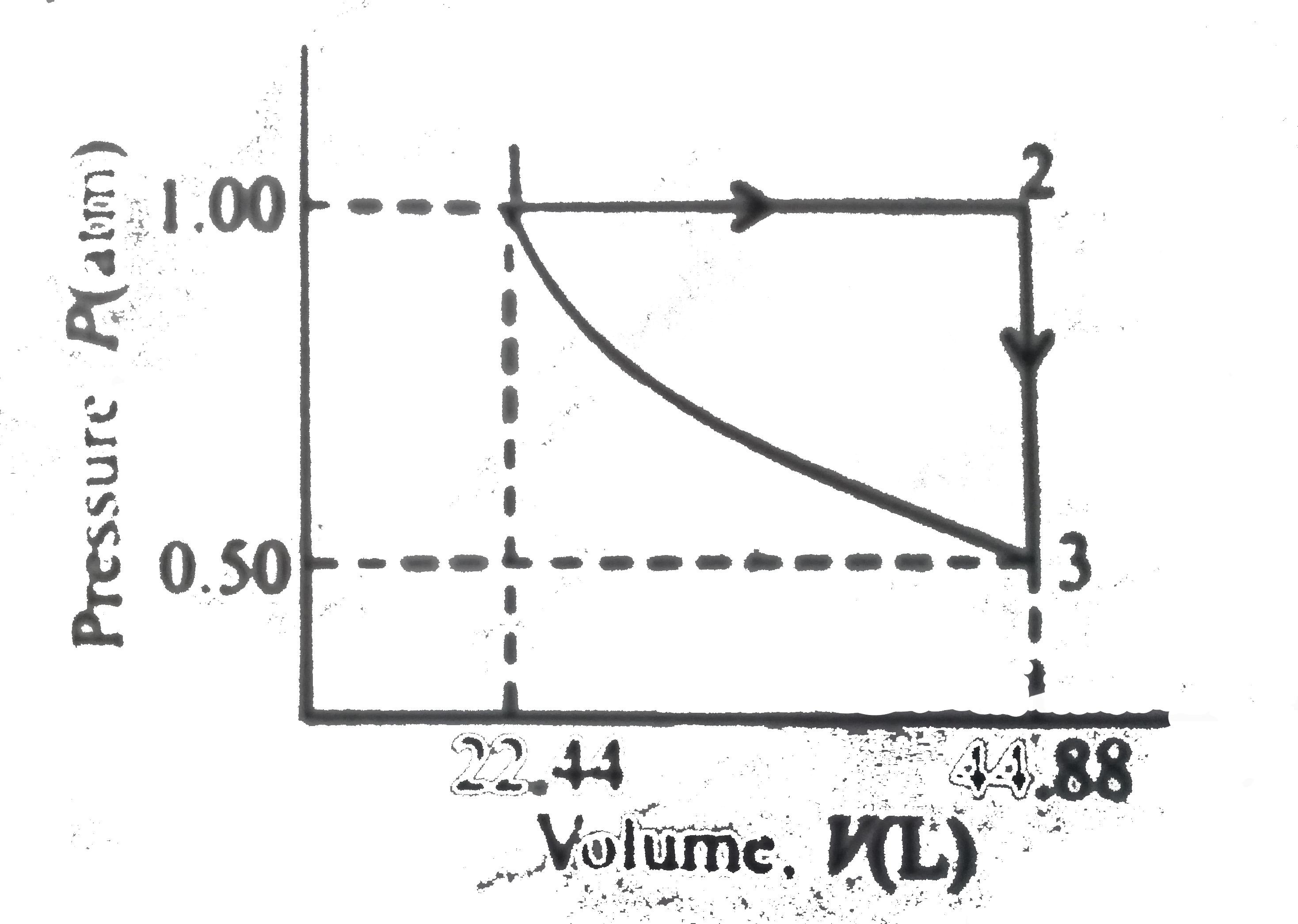
`DeltaH` for the overall cycle is
View SolutionA sample consisting of `1mol` of a mono-atomic perfect gas `(C_(V) = (3)/(2)R)` is taken through the cycle as shown.
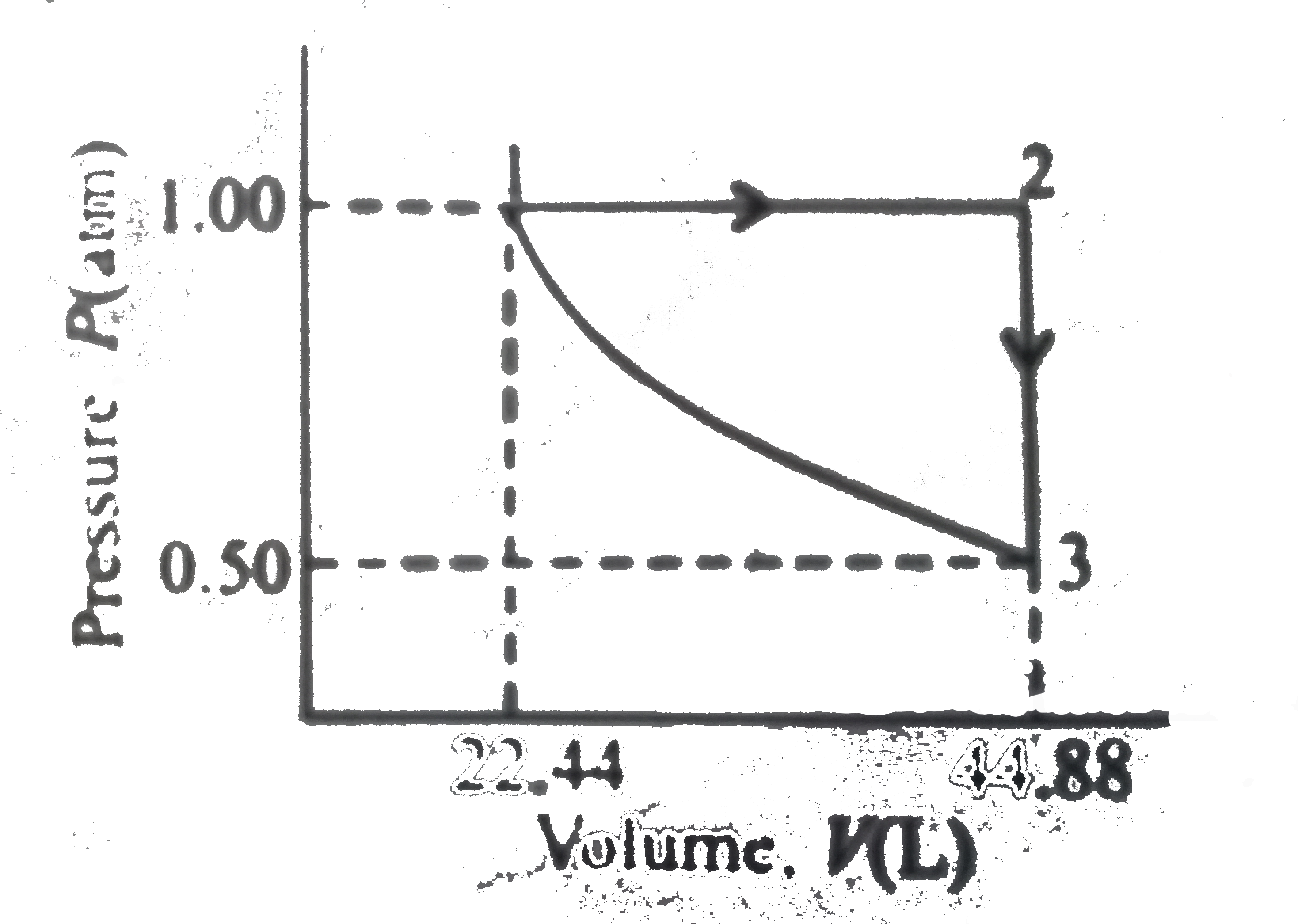
`DeltaU` for the process` (1 rarr2)` is
View SolutionA sample consisting of `1mol` of a mono-atomic perfect gas `(C_(V) = (3)/(2)R)` is taken through the cycle as shown.
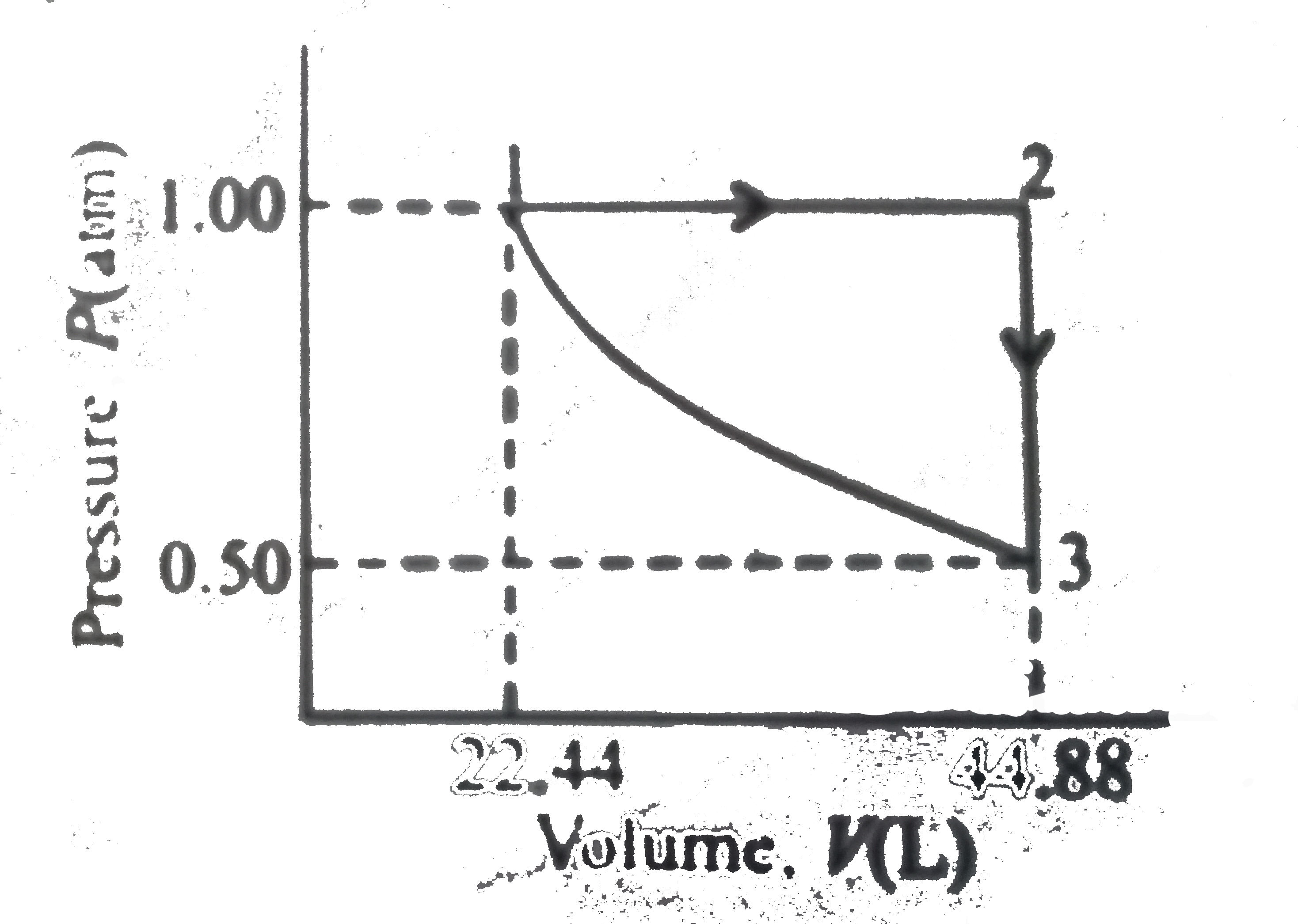
`DeltaU` for the process `(2 rarr 3)` is
View SolutionChemical reactions are invariably associated with the transfter of energy either in the form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
`{:(q = ms DeltaT,,s ="Specific heat"),(=cDeltaT,,c ="Heat capacity"):}`
Heat of reaction at constant volume is measured using bomb calorimeter.
`q_(V) = DeltaU =` Internal energy change
Heat of reaction at constant pressure is measured using simple or water calorimeter.
`q_(p) = DeltaH`
`q_(p) = q_(V) +P DeltaV`
`DeltaH = DeltaU +DeltanRT`
The heat capacity of a bomb calorimeter is `500 JK^(-1)`. When `0.1g` of methane was burnt in this calorimeter, the temperature rose by `2^(@)C`. The value of `DeltaU` per mole will be
View SolutionChemical reactions are invariably associated with the transfter of energy either in the form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
{:(q = ms DeltaT,,s =Specific heat),(=cDeltaT,,c =Heat capacity):}`
Heat of reaction at constant volume is measured using bomb calorimeter.
`q_(V) = DeltaU =` Internal energy change
Heat of reaction at constant pressure is measured using simple or water calorimeter.
`q_(p) = DeltaH`
`q_(p) = q_(V) +P DeltaV`
`DeltaH = DeltaU +DeltanRT`
For which reaction will `DeltaH = DeltaU`? Assume each reaction is carried out in an open container.
View SolutionChemical reactions are invariably associated with the transfter of energy either in the form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
`{:(q = ms DeltaT,,s ="Specific heat"),(=cDeltaT,,c ="Heat capacity"):}`
Heat of reaction at constant volume is measured using bomb calorimeter.
`q_(V) = DeltaU =` Internal energy change
Heat of reaction at constant pressure is measured using simple or water calorimeter.
`q_(p) = DeltaH`
`q_(p) = q_(V) +P DeltaV`
`DeltaH = DeltaU +DeltanRT`
What value of `DeltaT` should be used for the calorimetry experiment that gives the following graphical results?
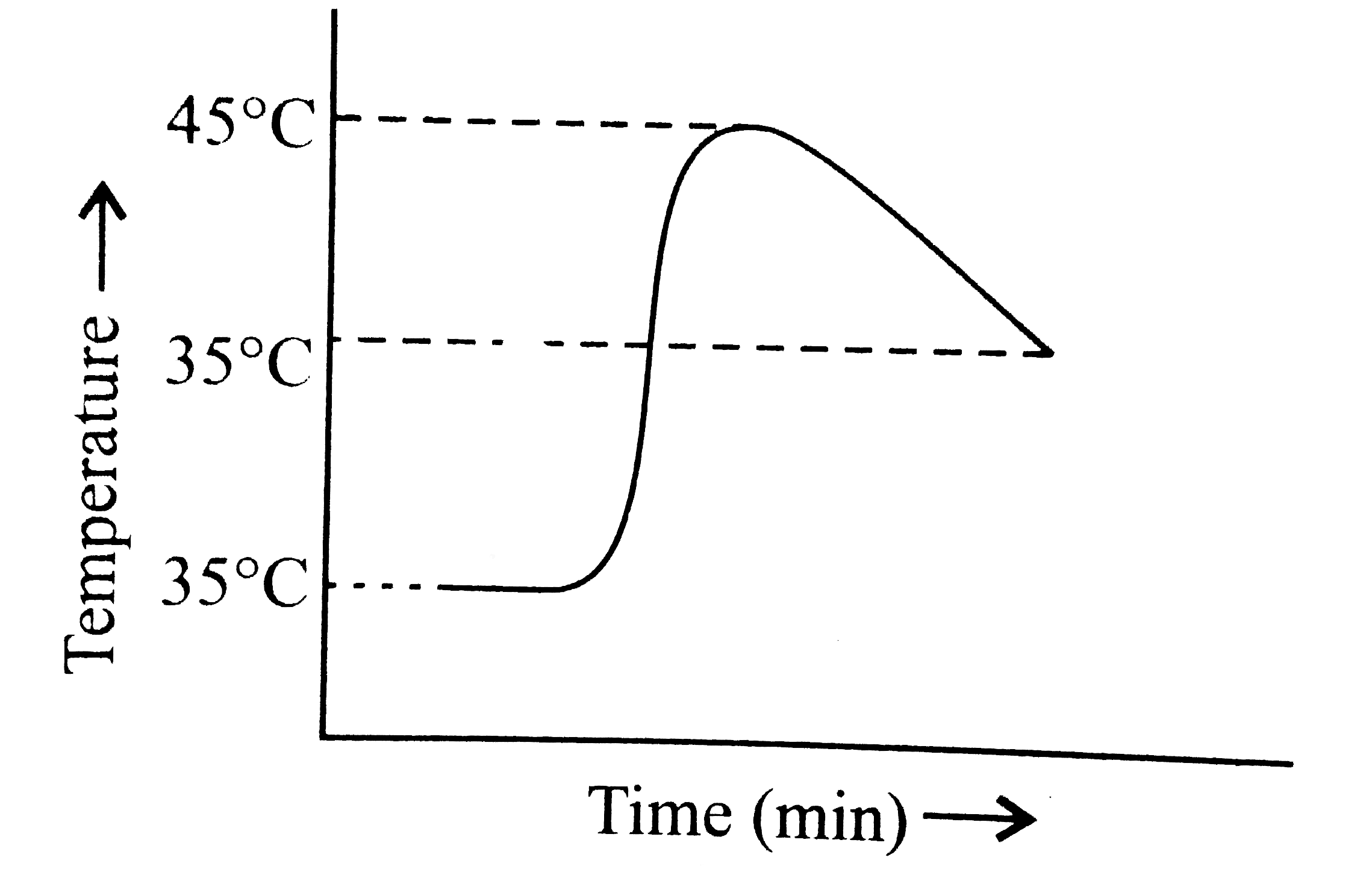
View SolutionChemical reactions are invariably associated with the transfter of energy either in the form of heat or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as
`{:(q = ms DeltaT,,s ="Specific heat"),(=cDeltaT,,c ="Heat capacity"):}`
Heat of reaction at constant volume is measured using bomb calorimeter.
`q_(V) = DeltaU =` Internal energy change
Heat of reaction at constant pressure is measured using simple or water calorimeter.
`q_(p) = DeltaH`
`q_(p) = q_(V) +P DeltaV`
`DeltaH = DeltaU +DeltanRT`
The enthalpy of fusion of ice is `6.02 kJ mol^(-1)`. The heat capacity of water is `4.18 J g^(-1)C^(-1)`. What is the smallest number of ice cubes at `0^(@)C`, each containing one molw of water, the are needed to cool `500g` of liquid water from `20^(@)C to 0^(@)C`?
View SolutionBond energies can be obtained by using the following relation: `DeltaH (reaction) = sum`Bond energy of bonds, broken in the reactants `-sum` Bond energy fo bonds, formed in the products
Bond enegry depends on three factors:
a. Greater is the bond length, lesser is the bond enegry.
b. Bond energy increases with the bond multiplicity.
c. Bond enegry increases with electronegativity difference between the bonding atoms.
Arrange `N -H, O - H`, and `F -H` bonds in teh decreasing order of bond enegry.
View SolutionBond energies can be obtained by using the following relation: `DeltaH (reaction) = sum`Bond energy of bonds, broken in the reactants `-sum` Bond energy fo bonds, formed in the products
Bond enegry depends on three factors:
a. Greater is the bond length, lesser is the bond enegry.
b. Bond energy increases with the bond multiplicity.
c. Bond enegry increases with electronegativity difference between the bonding atoms.
Bond enegry of differene halogen molecules will lie in the sequences
View SolutionBond energies can be obtained by using the following relation: `DeltaH (reaction) = sum`Bond energy of bonds, broken in the reactants `-sum` Bond energy fo bonds, formed in the products
Bond enegry depends on three factors:
a. Greater is the bond length, lesser is the bond enegry.
b. Bond energy increases with the bond multiplicity.
c. Bond enegry increases with electronegativity difference between the bonding atoms.
Which among the following sequences is correct about the bond enegry of `C -C, C=C` and `C -= C` bonds?
View SolutionBond energies can be obtained by using the following relation: `DeltaH (reaction) = sum`Bond energy of bonds, broken in the reactants `-sum` Bond energy fo bonds, formed in the products
Bond enegry depends on three factors:
a. Greater is the bond length, lesser is the bond enegry.
b. Bond energy increases with the bond multiplicity.
c. Bond enegry increases with electronegativity difference between the bonding atoms.
In `CH_(4)` molecule, which of the following statement is correct about the `C -H` bond enegry?
View SolutionBond energies can be obtained by using the following relation: `DeltaH (reaction) = sum`Bond energy of bonds, broken in the reactants `-sum` Bond energy fo bonds, formed in the products
Bond enegry depends on three factors:
a. Greater is the bond length, lesser is the bond enegry.
b. Bond energy increases with the bond multiplicity.
c. Bond enegry increases with electronegativity difference between the bonding atoms.
Use the bond enegries to estimate `DeltaH` for this reaction:
`H_(2)(g) +O_(2)(g) rarr H_(2)O_(2)(g)`
`{:("Bond","Bond energy"),(H-H,436 kJ mol^(-1)),(O-O,142 kJ mol^(-1)),(O=O, 499kJ mol^(-1)),(H-O,460kJ mol^(-1)):}`
View SolutionBond energies can be obtained by using the following relation: `DeltaH (reaction) = sum`Bond energy of bonds, broken in the reactants `-sum` Bond energy fo bonds, formed in the products
Bond enegry depends on three factors:
a. Greater is the bond length, lesser is the bond enegry.
b. Bond energy increases with the bond multiplicity.
c. Bond enegry increases with electronegativity difference between the bonding atoms.
The heat of formation of `NO` from its elements is `+90 kJ mol^(-1)`, What is the approximate bond dissociation enegry of the bond in `NO`?
`BE_(N=N) = 941 kJ mol^(-1) BE_(O=O) = 499 kJ mol^(-1)`
View SolutionA change in the free energy of a system at constant temperature and pressure will be:
`Delta_(sys)G = Delta_(sys)H -T Delta_(sys)S`
At constant temperature and pressure
`Delta_(sys) G lt 0` (spontaneous)
`Delta_(sys)G = 0` (equilibrium)
`Delta_(sys)G gt 0` (non-spontaneous)
The free enegry for a reaction having `DeltaH = 31400 cal, DeltaS = 32 cal K^(-1) mol^(-1) at 1000^(@)C` is
View SolutionA change in the free energy of a system at constant temperature and pressure will be:
`Delta_(sys)G = Delta_(sys)H -T Delta_(sys)S`
At constant temperature and pressure
`Delta_(sys) G lt 0` (spontaneous)
`Delta_(sys)G = 0` (equilibrium)
`Delta_(sys)G gt 0` (non-spontaneous)
For a spontaneous reaction `DeltaG`, equilibrium `K` and `E_(cell)^(Theta)` will be, respectively
View SolutionA change in the free energy of a system at constant temperature and pressure will be:
`Delta_(sys)G = Delta_(sys)H -T Delta_(sys)S`
At constant temperature and pressure
`Delta_(sys) G lt 0` (spontaneous)
`Delta_(sys)G = 0` (equilibrium)
`Delta_(sys)G gt 0` (non-spontaneous)
For a system in equilibrium, `DeltaG = 0`, under conditions of constant
View SolutionA change in the free energy of a system at constant temperature and pressure will be:
`Delta_(sys)G = Delta_(sys)H -T Delta_(sys)S`
At constant temperature and pressure
`Delta_(sys) G lt 0` (spontaneous)
`Delta_(sys)G = 0` (equilibrium)
`Delta_(sys)G gt 0` (non-spontaneous)
If both `DeltaH` and `Deltas` are negative, the reaction will be spontaneous
View SolutionIdentify the correct statement for change of Gibbs energy for a system `(Delta_(sys)G)` at constant temperature and pressure:
View Solution
Process `A rarr B` represents
View Solution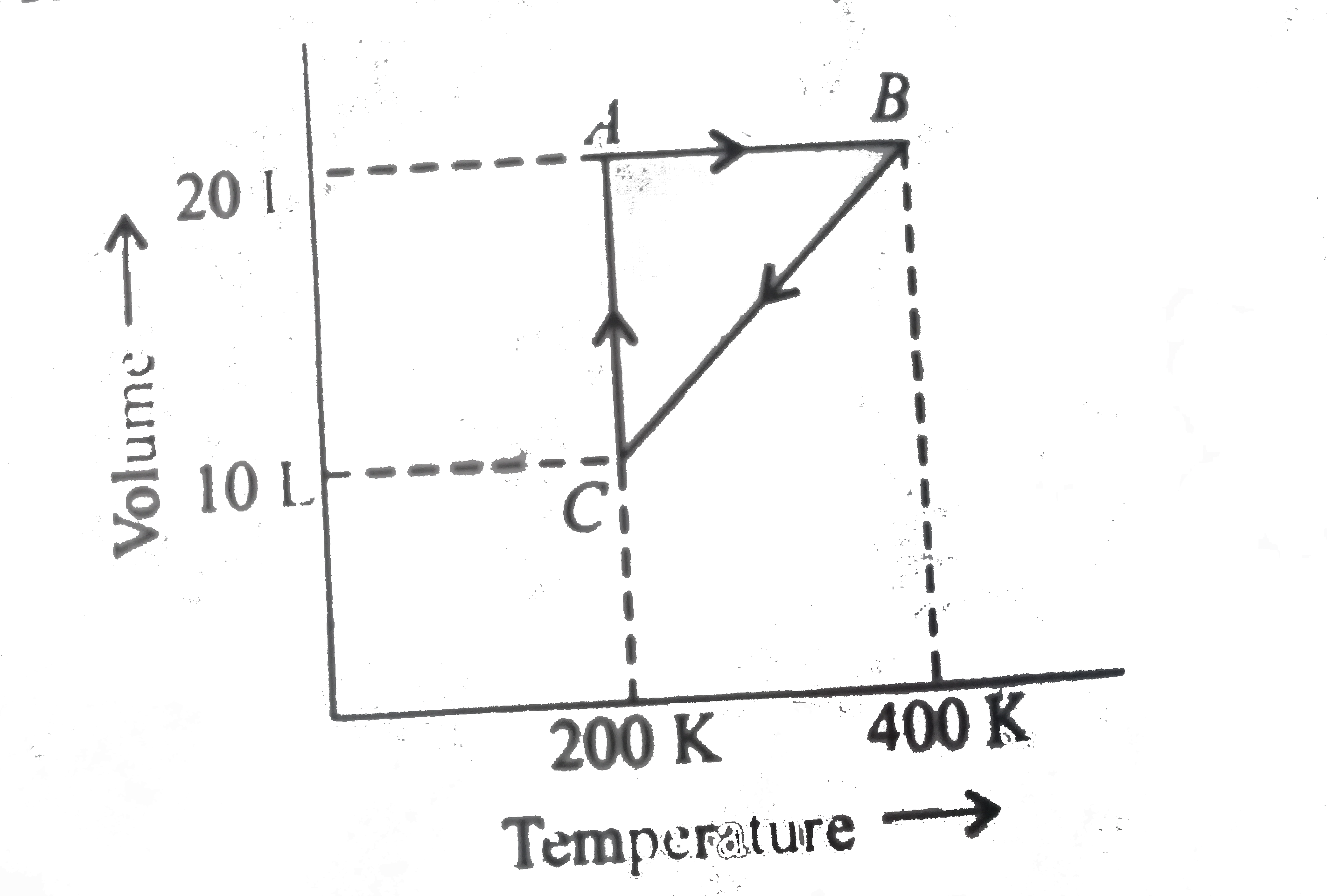
The pressure at `C` is
View Solution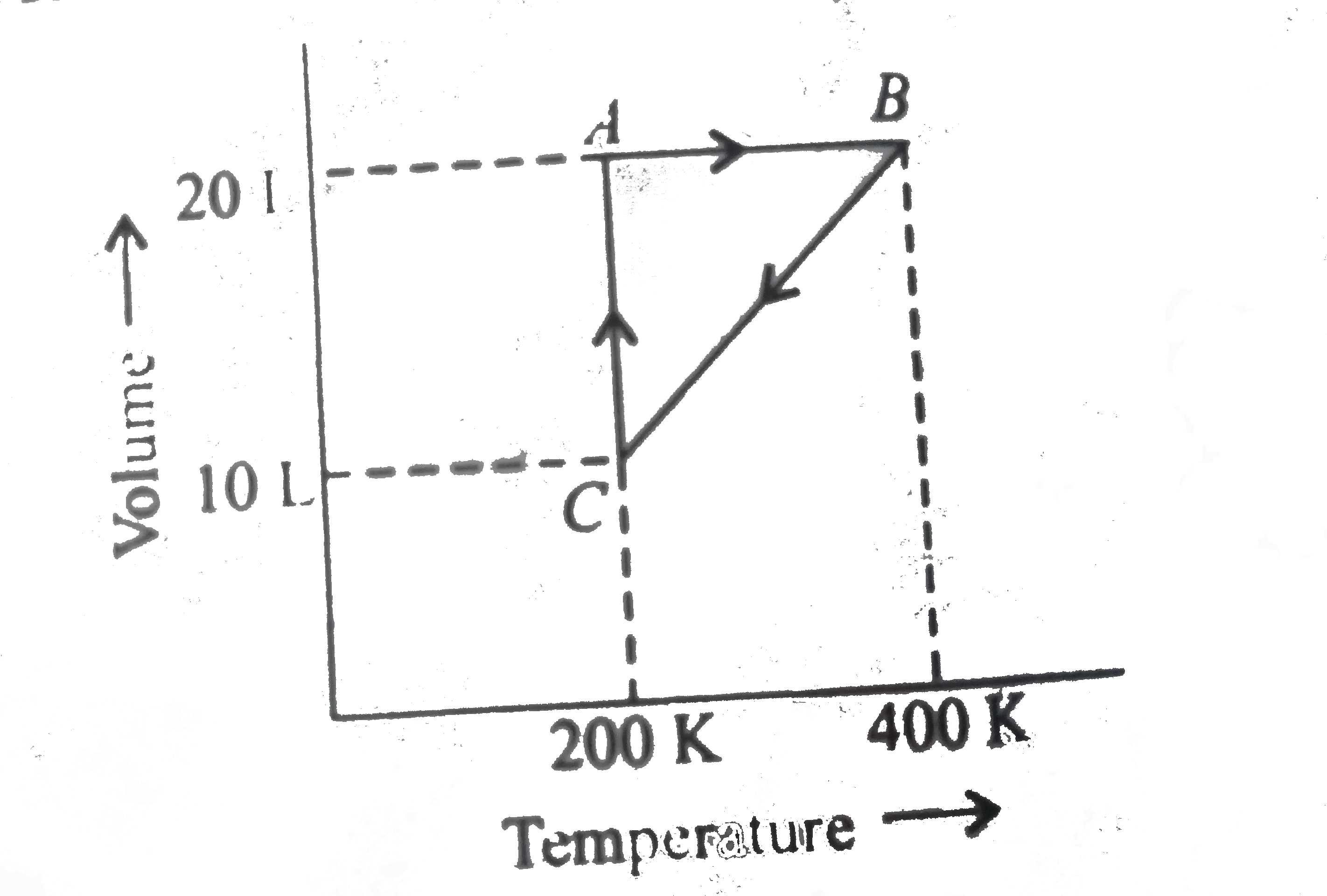
Work done in the process `C rarrA` is
View Solution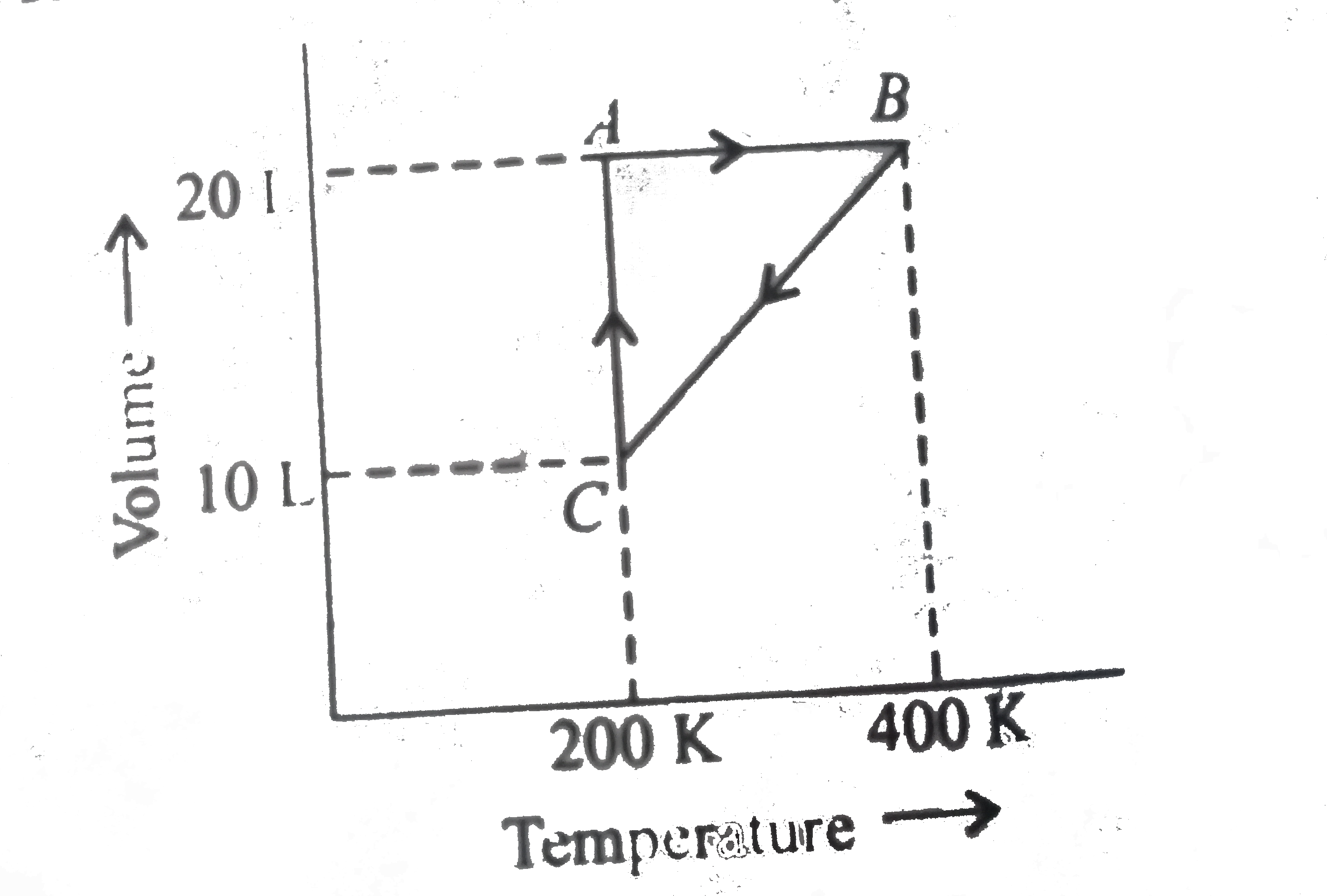
The process which occurs in going from `B rarr C` is
View Solution
The pressures at `A` and `B` in the atmosphere are, respectively,
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula `(DeltaS = DeltaH//T)`. In the reversible adiabatic process, however, `DeltaS` will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
`DeltaS = 2.303 C log (T_(1)//T_(2))`
The entropy change in an adiabatic process is
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula `(DeltaS = DeltaH//T)`. In the reversible adiabatic process, however, `DeltaS` will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
`DeltaS = 2.303 C log (T_(1)//T_(2))`
If water in an insulated vessel at `-10^(@)C` suddenly freezes, the entropy change of the system will be
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula `(DeltaS = DeltaH//T)`. In the reversible adiabatic process, however, `DeltaS` will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
`DeltaS = 2.303 C log (T_(1)//T_(2))`
The melting point of a solid is `200K` and its latent heat of fusion is `400cal mol^(-1)`. The entropy changes for the fusion of `1` mole of the solid (in cal `K^(-1))` at the same temperature would be
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula `(DeltaS = DeltaH//T)`. In the reversible adiabatic process, however, `DeltaS` will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
`DeltaS = 2.303 C log (T_(1)//T_(2))`
For which of the following cases, `DeltaS = (DeltaH)/(T)`?
View SolutionThe thermodynamic property that measures the extent of molecular disorder is called entropy. Entropy change of phase transformation can be calculated using Trouton's formula `(DeltaS = DeltaH//T)`. In the reversible adiabatic process, however, `DeltaS` will be zero. the rise in temperature in isobaric and isochoric conditions is found to increase the randomness or entropy of the system.
`DeltaS = 2.303 C log (T_(1)//T_(2))`
When `1` mol of an ideal gas is compressed to half of its volume, its temperature becomes double. Then the change in entropy `(DeltaS)` would be
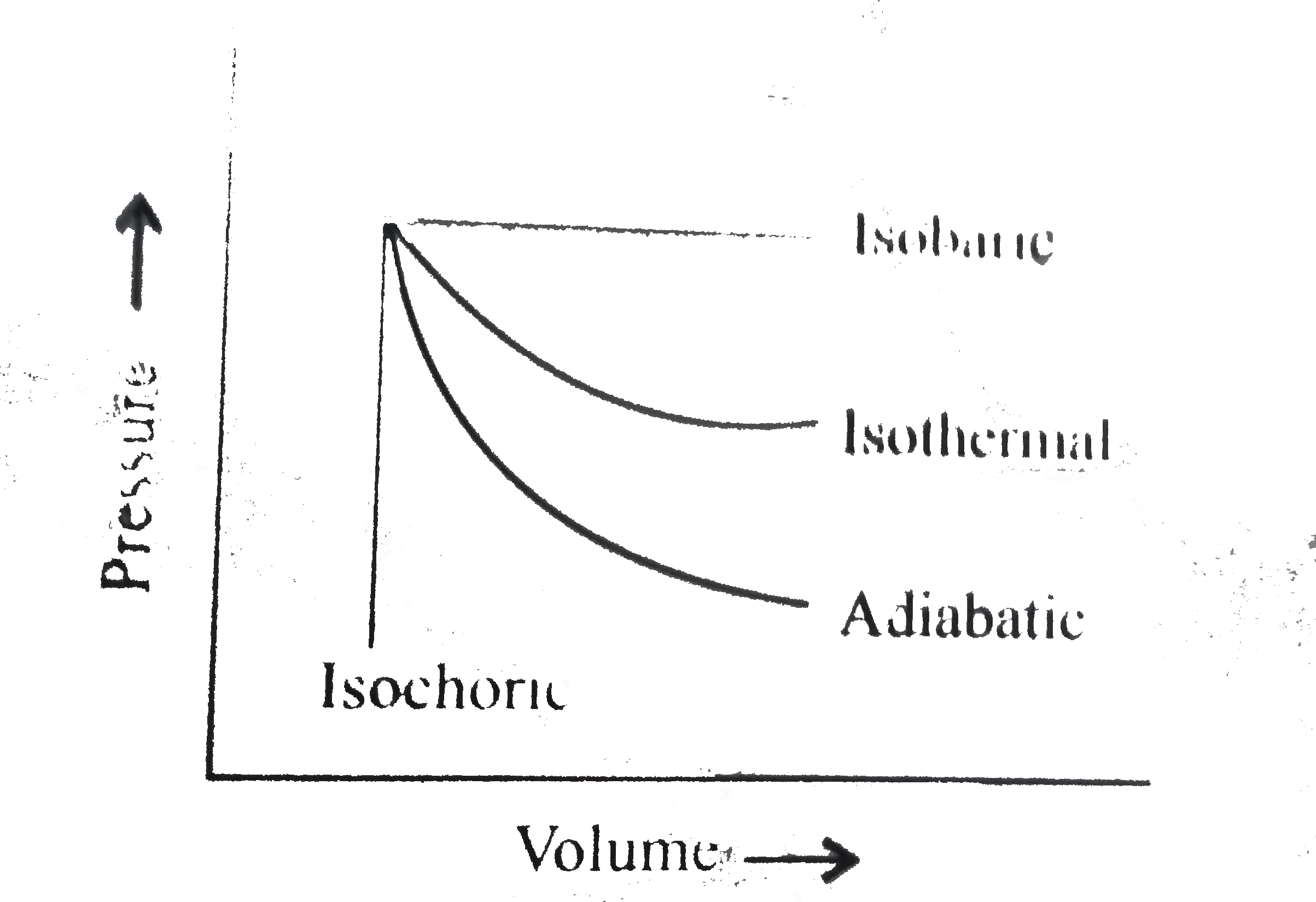
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:
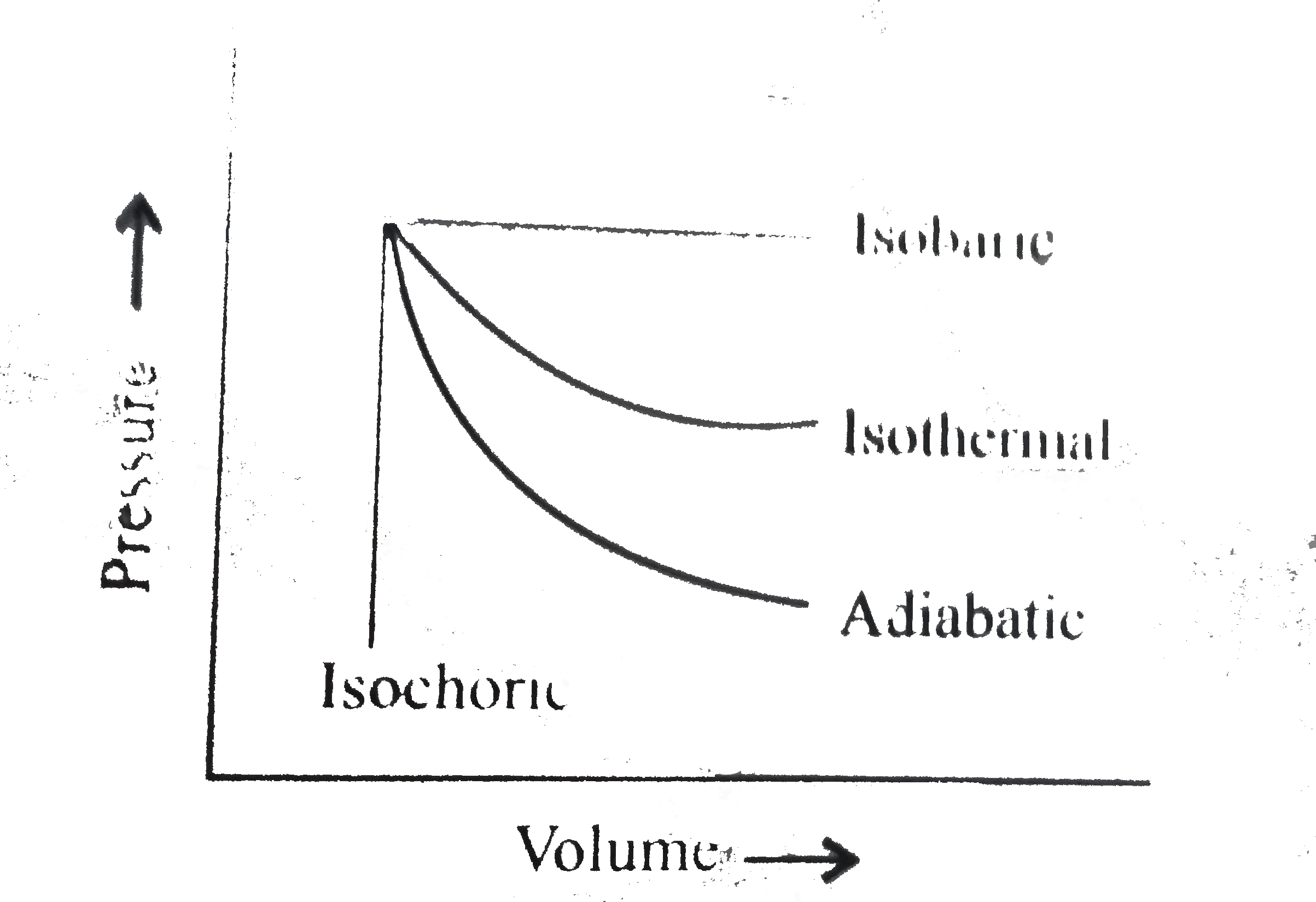
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
`w_(rev) gt w_(irr)`
The works of isothermal and adiabatic processes are different from each other.
`w_("isothermal reversible") = 2.303 nRT log_(10) ((V_(2))/(V_(1)))`
`= 2.303 nRT log_(10)((P_(2))/(P_(1)))`
`w_("adiabatic reversible") = C_(V) (T_(1)-T_(2))`
If `w_(1),w_(2),w_(3)` and `w_(4)` are work done in isothermal, adiabatic, isobaric, and isochoric reversible processes, respectively then the correct sequence (for expansion) would be
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:

Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
`w_(rev) gt w_(irr)`
The works of isothermal and adiabatic processes are different from each other.
`w_("isothermal reversible") = 2.303 nRT log_(10) ((V_(2))/(V_(1)))`
`= 2.303 nRT log_(10)((P_(2))/(P_(1)))`
`w_("adiabatic reversible") = C_(V) (T_(1)-T_(2))`
A thermodynamic system goes in a cyclic process as represented in the following `P -V` diagram:

The network done during the complete cycle is given by the area
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:

Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
`w_(rev) gt w_(irr)`
The works of isothermal and adiabatic processes are different from each other.
`w_("isothermal reversible") = 2.303 nRT log_(10) ((V_(2))/(V_(1)))`
`= 2.303 nRT log_(10)((P_(2))/(P_(1)))`
`w_("adiabatic reversible") = C_(V) (T_(1)-T_(2))`
`P-V` plots for two gases during adiabatic processes are given in the given figure:
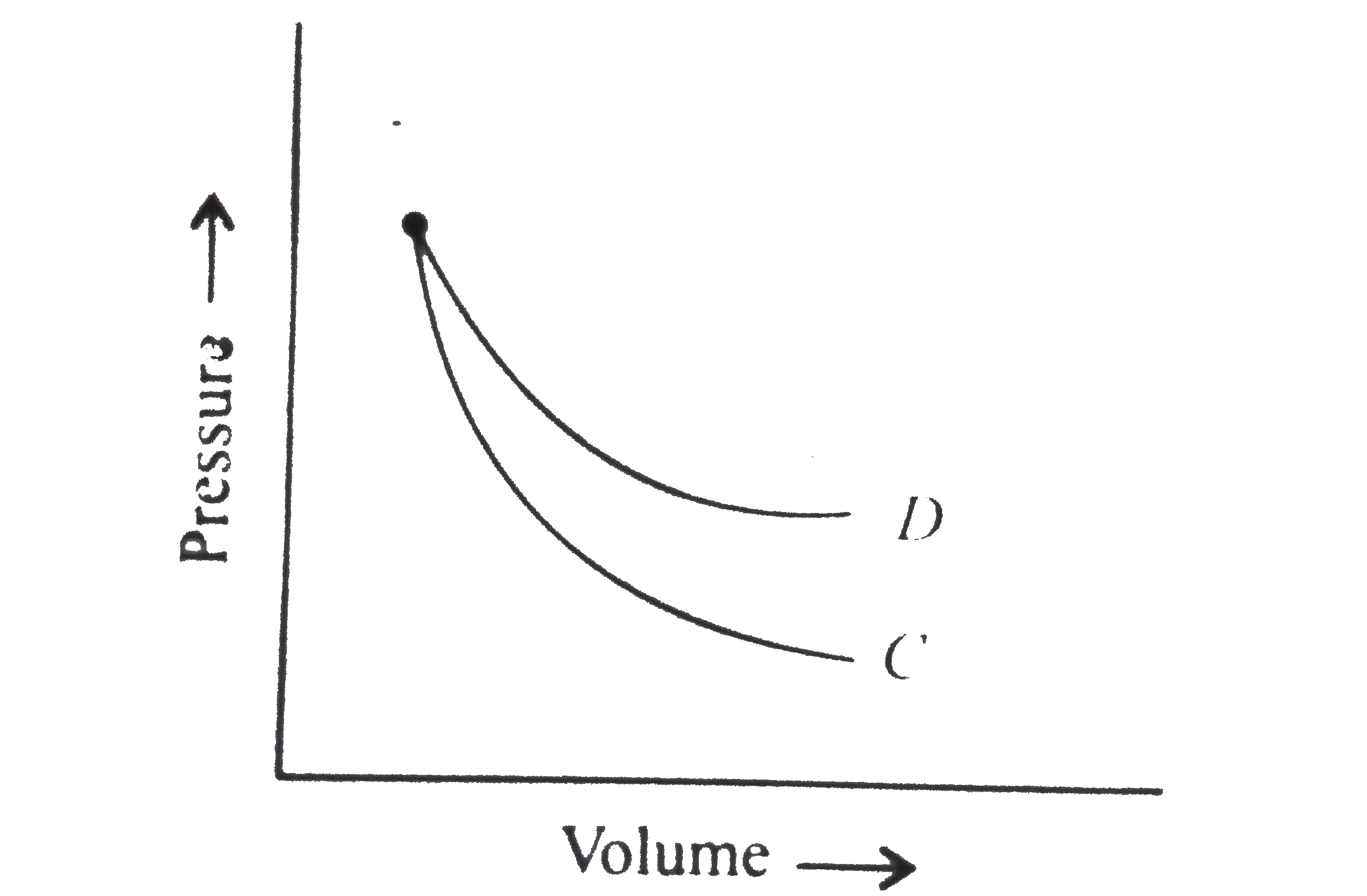
Plot `D` and Plot `C` should correspond to
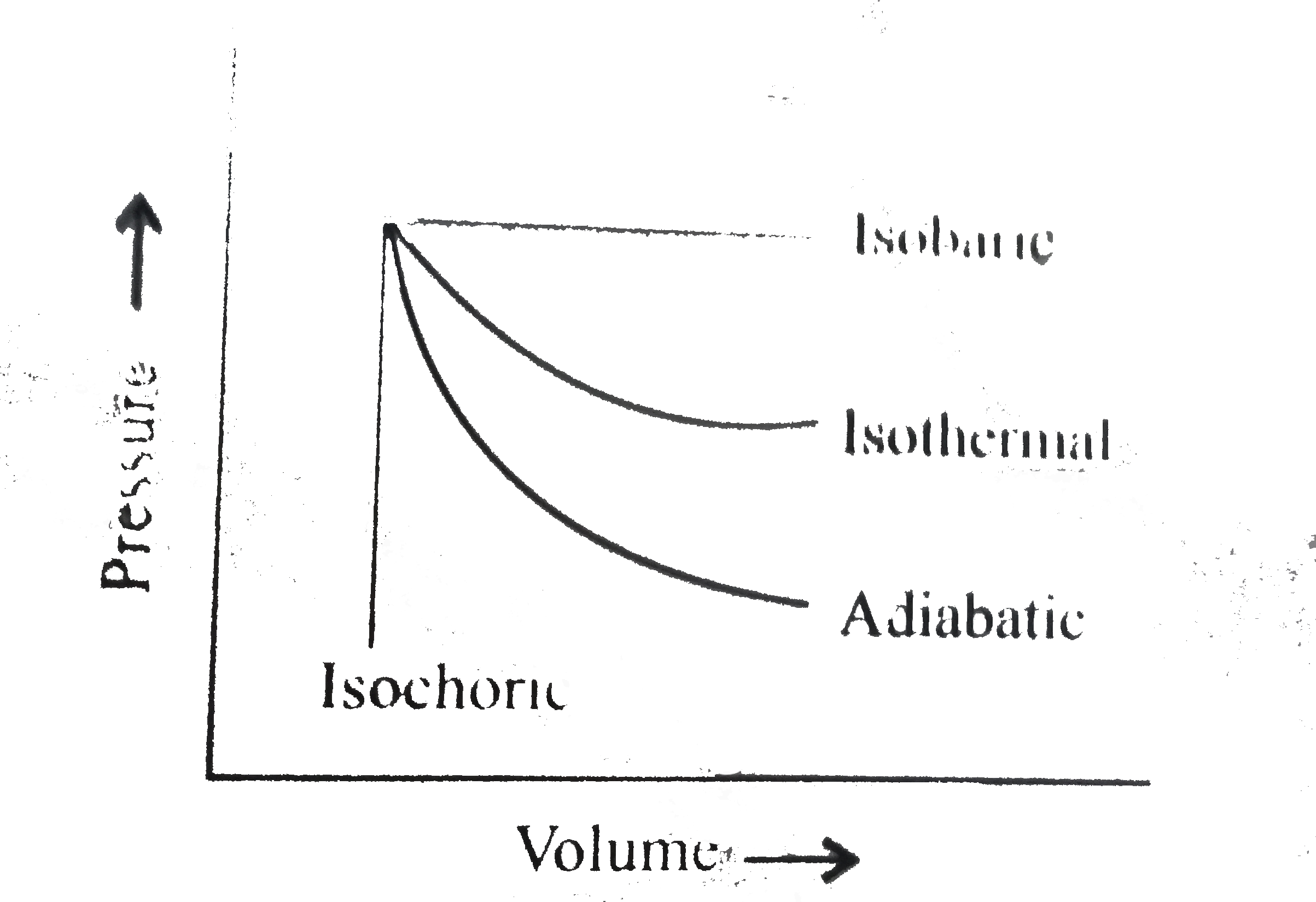
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
`w_(rev) gt w_(irr)`
The works of isothermal and adiabatic processes are different from each other.
`w_("isothermal reversible") = 2.303 nRT log_(10) ((V_(2))/(V_(1)))`
`= 2.303 nRT log_(10)((P_(2))/(P_(1)))`
`w_("adiabatic reversible") = C_(V) (T_(1)-T_(2))`
The `q` value and work done in isothermal reversible expansion of one mole of an ideal gas from initial pressure of `1` bar to final pressure of `0.1` bar at constant temperature `273K` are:
View SolutionThe pressure-volume of varies thermodynamic process is shown in graphs:
Work is the mole of transference of energy. It has been observed that reversible work done by the system is the maximum obtainable work.
`w_(rev) gt w_(irr)`
The works of isothermal and adiabatic processes are different from each other.
`w_("isothermal reversible") = 2.303 nRT log_(10) ((V_(2))/(V_(1)))`
`= 2.303 nRT log_(10)((P_(2))/(P_(1)))`
`w_("adiabatic reversible") = C_(V) (T_(1)-T_(2))`
Calculate work done when `1` mole of an ideal gas is expanded reversibly form `30L` to `60L` at a constant temperature of `300k`
View Solution
Exercises (Linked Comprehension) questions and complete solutions for chapter THERMODYNAMICS of CENGAGE CHEMISTRY (HINGLISH) of Class 11
All Exercises from CENGAGE CHEMISTRY Class 11 CHEMISTRY THERMODYNAMICS
- Archives (Assertion-Reasoning)
- Archives (Fill In The Blanks)
- Archives (Interger)
- Archives (Multiple Correct)
- Archives (Single Correct)
- Archives (Subjective)
- Archives (True/False)
- Ex 6.1
- Ex 6.2
- Ex 6.3
- Ex 6.4
- Ex 6.5
- Exercises (Assertion-Reasoning)
- Exercises (Fill In The Blanks)
- Exercises (Interger)
- Exercises (Linked Comprehension)
- Exercises (Multiple Correct)
- Exercises (Single Correct)
- Exercises (Subjective)
- Exercises (True/False)
- Solved Examples