Complete Solutions to Exercises Linked Comprehension of chapter ATOMIC STRUCTURE of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | ATOMIC STRUCTURE |
| CENGAGE CHEMISTRY | Exercises Linked Comprehension |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The atomic number of chromium is `24` Its electronic coefigueration in ground state in `1s^(2) 2s^(2)2p^(6)3s^(2)4s^(1) 3d^(5)` .Chromium atom by using `3` electron from `Cr ^(3+)` .A chromium atom contain `17%` morte neutron than the proton. Now answer the following questions
The number of unpaired electron in `Cr ^(3+)`ion is
View SolutionThe atomic number of chromium is `24` Its electronic configuration in ground state in `1s^(2) 2s^(2)2p^(6)3s^(2)3p^(6)4s^(1) 3d^(5)` Now answer the following questions
The number of electron having `n = 3` and `m_(1) = 0` in chromium atom is
View SolutionAn atom has electronic configuration `1s^(2),2s^(2),2p^(6),3s^(2),3d^(3),4s^(2)` you will place it in
View SolutionThe atomic number of chromium is `24` .A chromium atom contain `17%` more neutron than the proton. The element atom can be represented by the symbol
View SolutionThe atomic number of chromium is `24` Its electronic coefigueration in ground state in `1s^(2) 2s^(2)2p^(6)3s^(2)4s^(1) 3d^(5)` .Chromium atom by using `3` electron from `Cr ^(2+)` .A chromium atom contain `17%` morte neutron than the proton. Now answer the following questions
The number of occupied sub- shell in `Cr^(3+)` ion is
View SolutionAn atom has `2K,8L` and `5M` electron write its electronic configuration and answer the following:
View SolutionA neutral atom of an element has `2K,8L` and `5M` electron .Find out the following
Number of electron in valence shell
View SolutionA neutral atom of an element has `2K,8L` and `5M` electron .Find out the following
Number of unpaired electrons
View SolutionAn atom has `2K,8L` and `5M` electron write its electronic configuration and answer the following:
View SolutionA neutral atom of an element has `2K,8L` and `5M` electron .Find out the following
Maximum number of electron having same spin
View SolutionIn a mixture of `H - He^(+) gas (He^(+)` is singly ionized He atom), H atom and `He^(+)`ion are excited to their repectve first excite states. Subsequently , H atoms transfer their total excitation energy to `He^(+)`ion (by collisitions). Assume that the Bohr model of atom is exctly valid.
`n = 4 overset( H atom)___ 0.85 eV overset (He^(+) atom)_ - 3.4 eV`
`n = 3 to - 1.51 eV_ to - 6.04 eV`
`n = 2 to - 3.4 eV to - 13.6 eV`
`n = 1 to - 13.6 eV _to -= 54.4 eV`
The quamtum number `n` of the state finally populated in `He^(+)` ions in
View SolutionIn a mixture of `He^(Theta)` gas H atom and `He^(Theta)` ions Are excited to three respective first excited subsepuenly , H atom transfers its total excitation energy to `He^(Theta)`ions by collision .Assuming that Bohr model of an atom is applicable , answer the following question
The wavelength of the light amitted in the visible region by `He^(Theta)` ions qaafter collisions with `He^(Theta)`ion is
View SolutionIn a mixture of `He^(o+)` gas H atom and `He^(o+)` ions Are excited to three respective first excited subsepuenly , H atom transfers its total excitation energy to `He^(o+)`ions by collision .Assuming that Bohr model of an atom is applicable , answer the following question
The ratio of teh potential energy of the `n = 2` electron for H atom to the of `He^(o+)` ion is
View SolutionIn a mixture of `He^(o+)` gas H atom and `He^(o+)` ions Are excited to three respective first excited subsepuenly , H atom transfers its total excitation energy to `He^(o+)`ions by collision .Assuming that Bohr model of an atom is applicable , answer the following question
If each hydrogen atom in the ground state of `1.0 mol ` of H atom is excited by absorbing photon of energy `8.4 eV, 12.09 eV` and `15.0 eV` of energy then the number of spectral lines emitted is equal to
View SolutionIn a mixture of `H - He^(+) gas (He^(+)` is singly ionized He atom), H atom and `He^(+)`ion are excited to their repectve first excite states. Subsequently , H atoms transfer their total excitation energy to `He^(+)`ion (by collisitions). Assume that the Bohr model of atom is exctly valid.
`n = 4 overset( H atom)___ 0.85 eV overset (He^(+) atom)_ - 3.4 eV`
`n = 3 to - 1.51 eV_ to - 6.04 eV`
`n = 2 to - 3.4 eV to - 13.6 eV`
`n = 1 to - 13.6 eV _to -= 54.4 eV`
The ratio of the kinetic energy of the `n = 2` electron for the H atom to that of `He^(+)`ion is
View SolutionConsider a system containing a negatively charge point `(pi, m_(pi) = 273m_(e))` orbital around a stationary nucleus of atomic number Z .The total energy `(E_(n))` of ion is half of its potential energy `(PE_(n))` in nth stationary state .The motion of the point can be assumed to be in a uniform circular motion with centripetal force given by the force of attraction between the positive nucleus and the point .Assume that point revolves only in the stationary state defined by the quantization of its angular momentum about the nucleus as Bohr's model
The potential energy `(PE_(n))` of ion follows:
View SolutionConsider a system containing a negatively charge point `(pi, m_(pi) = 273m_(e))` orbital around a stationary nucleus of atomic number Z .The total energy `(E_(n))` of ion is half of its potential energy `(PE_(n))` in nth stationary state .The motion of the point can be assumed to be in a uniform circular motion with centripetal force given by the force of attraction between the positive nucleus and the point .Assume that point revolves only in the stationary state defined by the quantization of its angular momentum about the nucleus as Bohr's model
Number of waves made by the point when it orbits in third excitation state are
View SolutionConsider a system containing a negatively charge poin `(pi, m_(pi) = 273^(@)m_(e))` orbital around a staionary nucleus of atomic number Z .The total energy `(E_(n))` of ion is half of its potential energy `(PE_(n))` in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The longest wavelength radiation emitted in the emission spectrum when the pion de-excited from `n = 3` to ground state lies which of the following region ?
View SolutionConsider a system containing a negatively charge poin `(pi, m_(pi) = 273^(@)m_(e))` orbital around a staionary nucleus of atomic number Z .The total energy `(E_(n))` of ion is half of its potential energy `(PE_(n))` in nth sationary state .The motion of the poin can be assumed to be in a uniform circular notion with centripents force given by the force of attaraction between the positive uncless and the point .Assume that point revolves only in the stationary satte defined by the quantisation of its angular momentum about the nucless as Bohr's model
The wavelength `(lambda_(n))` of the pion orbital in nth stationarry state is ggiven by :
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited state of quantum number n. The excited atom can make a transition to the first excited state by successively emitting two photons of energy 10.2 eV and 17.0 eV, respectively. Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV, respectively Determine the values of n and Z. (lonization energy of H-atom = 13.6 eV)
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited state of quantum number n. The excited atom can make a transition to the first excited state by successively emitting two photons of energy 10.2 eV and 17.0 eV, respectively. Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV, respectively Determine the values of n and Z. (lonization energy of H-atom = 13.6 eV)
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited satte of quantum number n .This excited atom can make a transition to the first excited state by succesively emitting two photon of energies `10.20 eV` and `17.00 eV` .Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting twio photon of energy `4.25 ev` and `5.95 eV` Determine the followings:
The atom during transition from `n = 1` to `n = 2` emit radiation in the region of
View SolutionA hydrogen like species (atomic number Z) is present in a higher excited state of quantum number n. This excited atom can make a transitionn to the first excited state by successive emission of two photons of energies 10.20 eV and 17.0 eV respectively. Altetnatively, the atom from the same excited state can make a transition to the second excited state by successive of two photons of energy 4.25 eV and 5.95 eVv respectively. Determine the value of Z.
View SolutionThe characteristic X-rays for the lines of `K_(a)` series in element X and Y are `9.87 Å and 14.6 Å` respectively .If Moseley's equation `sqrt(v) = 4.9 xx 10^(7) (Z - 0.75)` is followed:
The atomic number of X is
View SolutionThe characteristic X-rays for the lines of `K_(a)` series in element X and Y are `9.87 Å and 14.6 Å` respectively .If Moseley's equation `sqrt(v) = 4.9 xx 10^(7) (Z - 0.75)` is followed:
The atomic number of Y is
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si `deltax.delta (mv)ge(h)/(4pi)`
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainty in velocity and position is same, then the uncertainty in momentum will be :
View SolutionIt is impossible to determine simultaneously the position of velocity of small microscopic particle such as electron , proton or neutron with accuracy .This is called Heisenberg's uncertainty principle. Mathematically, it is represented as `Delta x. Delta p ge (h)/(4pi) , Delta x` is uncertainty in position `Delta p ` is uncertainty in momentum.
View SolutionThe seqence of filling electgron in sub-shells of element with few exception in d-block and f-block element is govened by.Aufbau principle followed by Hund's rule and pauli's ecxclusion principal
a. The electron prefers to enter into sub-shell with lower `(n +l)` values
The energy for any sub-shell of an element other than hydrogen is praportioanal to the sum of principal quantum number (n) and angular momentum quantum number
b. If `(n + l)` value is same for many sub-shell with lowest n value
c. i. Fulfiling sub-shell is more stable
ii. Half filled sub-shell is more stable less than half filed
Which pair of sub-shell has same energy for above described excriptional element under rule (a) ?
View SolutionIf Hund's rule is not obeyed by some element given below then which atom has maximum magnetic moment
View SolutionThe sequence of filling electron in sub-shells of element with few exception in d-block and f-block element is governed by Aufbau principal followed by Hund's rule and pauli's exclusion principal
a. The electron prefers to enter into sub-shell with lower `(n +l)` values
The energy for any sub-shell of an element other than hydrogen is proportional to the sum of principal quantum number (n) and angular momentum quantum number
b. If `(n + l)` value is same for many sub-shell with lowest n value
c. i. Fulfilled sub-shell is most stable
ii. Half filled sub-shell is more stable less than half filed
Which pair of element follow rule (c ) (ii) ?
View SolutionThe sequence of filling electron in sub-shells of element with few exception in d-block and f-block element is governed by Aufbau principal followed by Hund's rule and pauli's exclusion principal
a. The electron prefers to enter into sub-shell with lower `(n +l)` values
The energy for any sub-shell of an element other than hydrogen is proportional to the sum of principal quantum number (n) and angular momentum quantum number
b. If `(n + l)` value is same for many sub-shell with lowest n value
c. i. Fulfilled sub-shell is most stable
ii. Half filled sub-shell is more stable less than half filed
Which pair of element follow rule (c ) (ii) ?
View SolutionThe sepence of filling electgron in sub-shells of element with few exception in d-block and f-block element is govemed by.Aufhau principal followed by Hand's rule and palli's ecxcited principal
a. The electron prefers to unter into sub-shell with lower `(n +1)` values
The energy for any sub-shell of an element other than hydrogen is preportioanal to the sum of principal quantum number (n) and angular momentum quantum number
b. If `(n + 1)` value is same for many sub-shell with lowest n value
c. i. Fulfiling sub-shell is more stable
ii. Half filled sub-shell is more stable less than half filed
Which pair of element follow rulke (c ) (ii) ?
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to `(n(n - 1))/(2)`If teh electron comes back from the energy level having energy `E_(2)` to the energy level having energy `E_(1)` then the difference may be expresent in terms of energy of photon as `E_(2) - E_(1) = Delta E, lambda = hc//Delta E` Since h and c are constants `Delta E` coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula `bar v = RZ^(2)((1)/(n_(1)^(2))- (1)/(n_(12)^(2)))`Where R is a Rydherg constant
If the ionisation potential for hydrogen -like atom in a sample is ` 122.4 V` then the series limit of the paschen series for this atom is
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to `(n(n - 1))/(2)`If teh electron comes back from the energy level having energy `E_(2)` to the energy level having energy `E_(1)` then the difference may be expresent in terms of energy of photon as `E_(2) - E_(1) = Delta E, lambda = hc//Delta E` Since h and c are constants `Delta E` coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula `bar v = RZ^(2)((1)/(n_(1)^(2))- (1)/(n_(12)^(2)))`Where R is a Rydherg constant
Its a single isolated atom, an electrons make transition from fifth excited state is second thern maximum number of different type of photon observed is
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to `(n(n - 1))/(2)`If teh electron comes back from the energy level having energy `E_(2)` to the energy level having energy `E_(1)` then the difference may be expresent in terms of energy of photon as `E_(2) - E_(1) = Delta E, lambda = hc//Delta E` Since h and c are constants `Delta E` coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula `bar v = RZ^(2)((1)/(n_(1)^(2))- (1)/(n_(12)^(2)))`Where R is a Rydherg constant
The difference in the wavelength of the second line is Lyman series and last line of breaker series is a hydrogen sample is
View SolutionThe only element in the hydrogen atom resides under ordinary condition on the first orbit .When energy is supplied the element move to hjgher energy ornbit depending on the lower of energy absioerbed .When this electron to may of the electron return to any of the lower orbits, it emit energy Lyman series is formed when the electron to the lowest orbit white Balmer series ids formed when the electron returns to the second orbit similar Paschen Brackett, and Pfund series are formed when electron return to the third fourth , and fifth arbit from highest energy orbits, respectively
Maximum number of liner produced is equal when as electron jumps from nth level to ground level is equal to `(n(n - 1))/(2)`If teh electron comes back from the energy level having energy `E_(2)` to the energy level having energy `E_(1)` then the difference may be expresent in terms of energy of photon as `E_(2) - E_(1) = Delta E, lambda = hc//Delta E` Since h and c are constants `Delta E` coresponding to definite energy , thus , each transition from one energy level to unother will produce a light of definite wavelem=ngth .This isd actually observed as a line in the spectrum of hydrogen atom Wave number of line is given by the formula `bar v = RZ^(2)((1)/(n_(1)^(2))- (1)/(n_(12)^(2)))`Where R is a Rydherg constant
The wave number of electromagnetic radiation emitted during the transition of electron in between the two levels of `Li^(2+)` ion whose pricipal quantum numbner sum is `4` and difference is `2` is
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
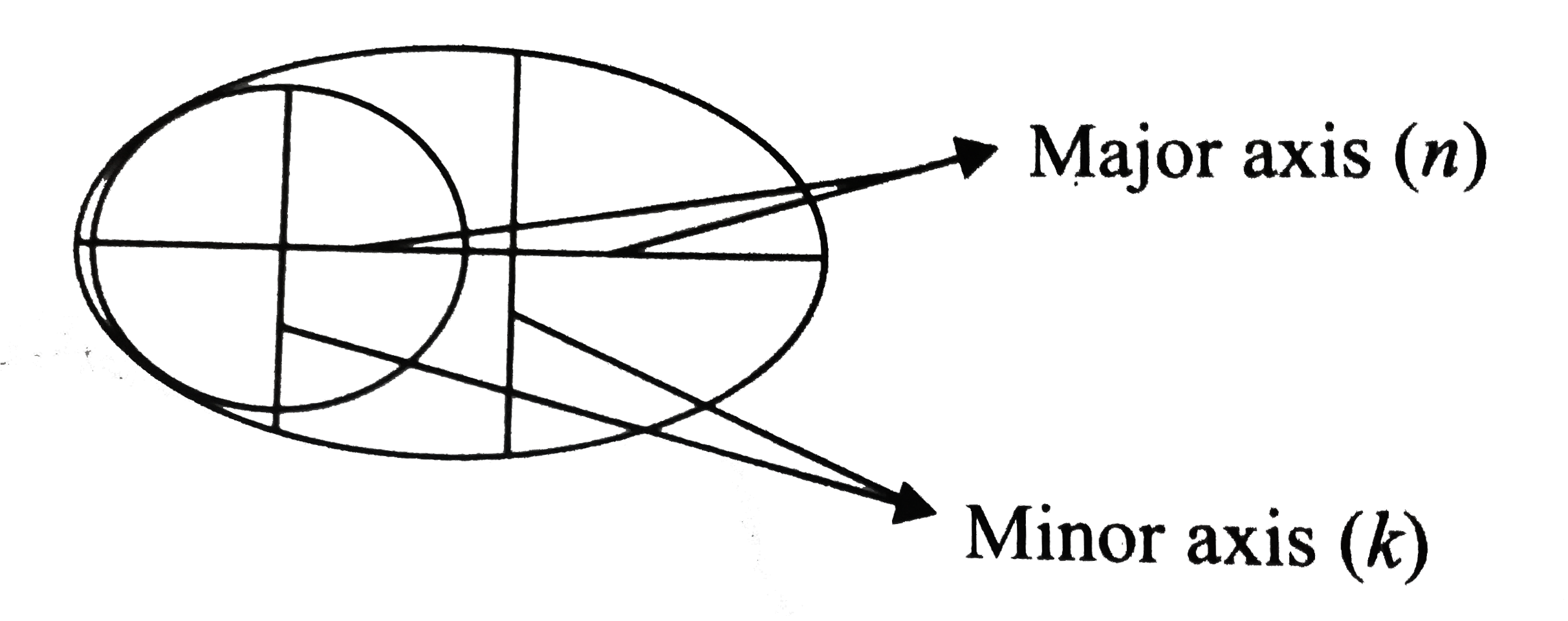
If n is the major axis and k is th e minor axis , then `n//k = 1` for circular shape white `n//k gt 1` for elliptical shape
Which value of n and k suggest about the shape of `3s` orbitsl?
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
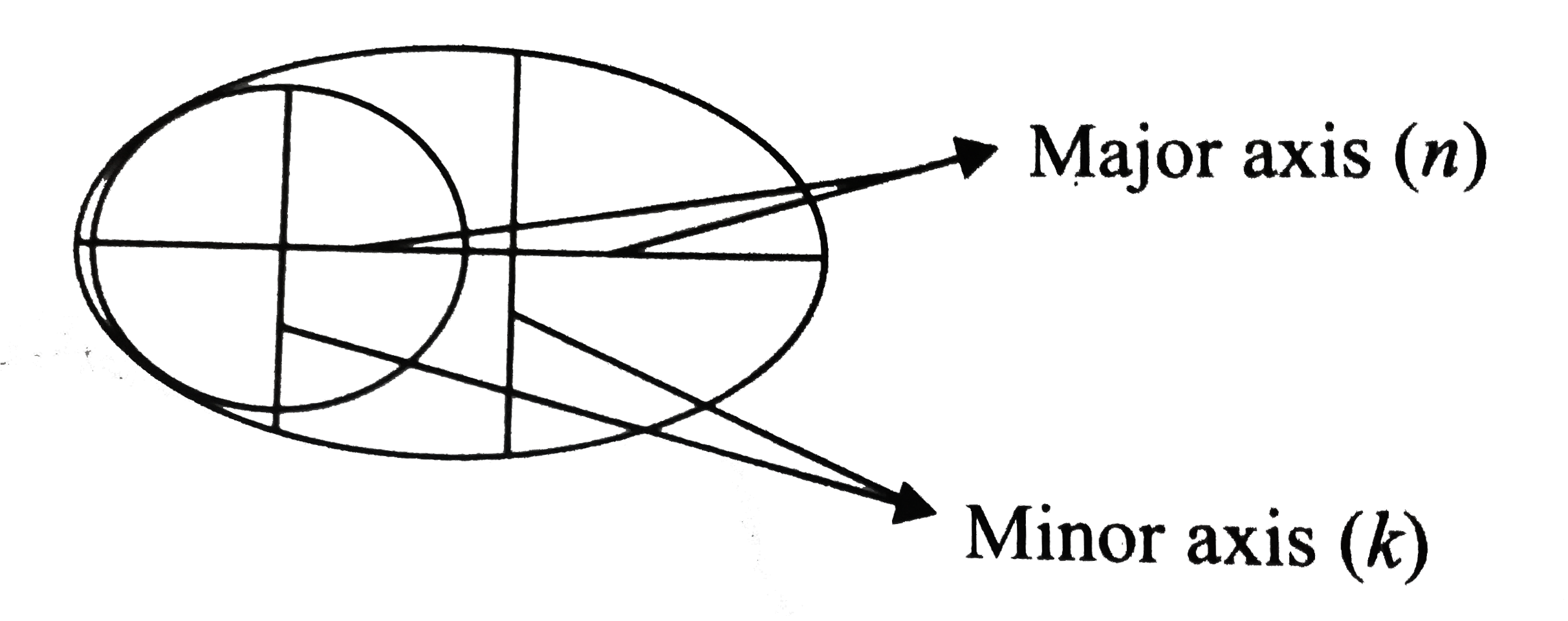
If n is the major axis and k is th e minor axis , then `n//k = 1` for circular shape white `n//k gt 1` for elliptical shape
Which shape is used to be circular having `n//k` value
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value

If n is the major axis and k is th e minor axis , then `n//k = 1` for circular shape white `n//k gt 1` for elliptical shape
Which shape is used to be circular having `n//k` value
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
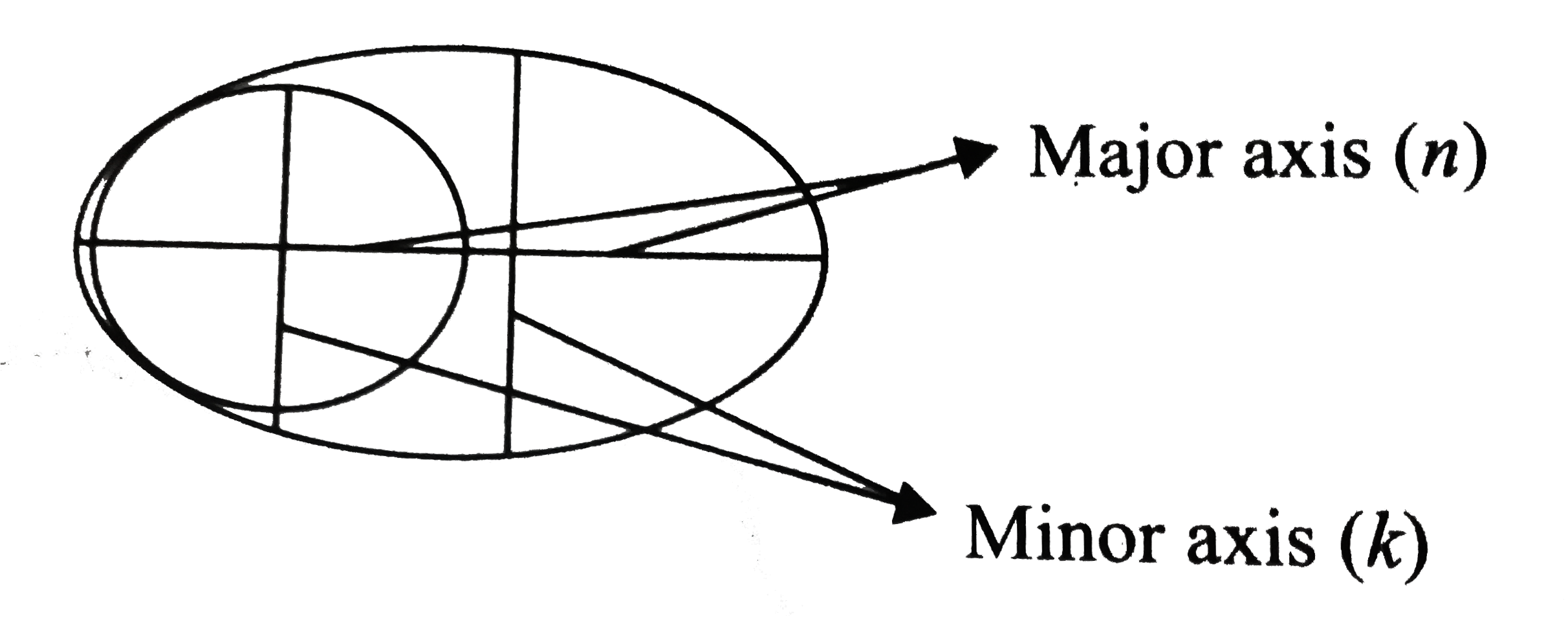
If n is the major axis and k is th e minor axis , then `n//k = 1` for circular shape white `n//k gt 1` for elliptical shape
Which orbit shape has highest `n//k gtgt 1` value?
View SolutionThe shape of orbitals are related to the ratio of principal quantum number (n) to substiary quantum number (k,a modifacation of Bohr-sommerfield theory ).The value of k for any shell has a value ranging betwe3en n to l .The amximum value for k is given for x sub-shell white k becomes with p, d,f........ repectively upto minimum value
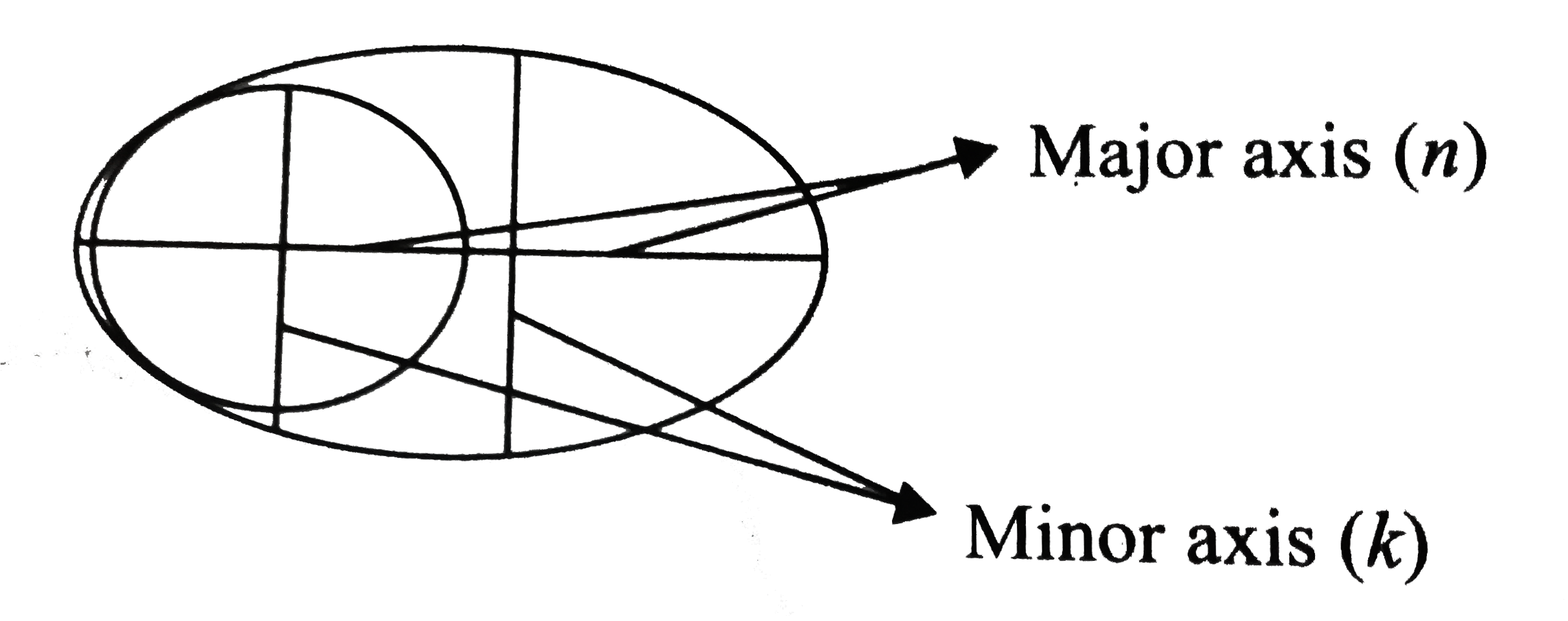
If n is the major axis and k is th e minor axis , then `n//k = 1` for circular shape white `n//k gt 1` for elliptical shape
Which is correct according to the increasing elliptical number of sub-shell ?
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectric effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejected electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Absorbed energy - Work function
`(1)/(2) mv_(max)^(2) = h(v) - h(v_(n)) = hv [(1)/(lambda) - (1)/(lambda_(n))]`
Where `v_(n)` and `lambda_(0)` are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if `V_(0)` is the stopping potential `eV_(0) = h(v- v_(0))`
In the photoelectric currect effect the shape of strainght line graph between stopping potential `(V_(0))` and frequency of incident light (V) gves
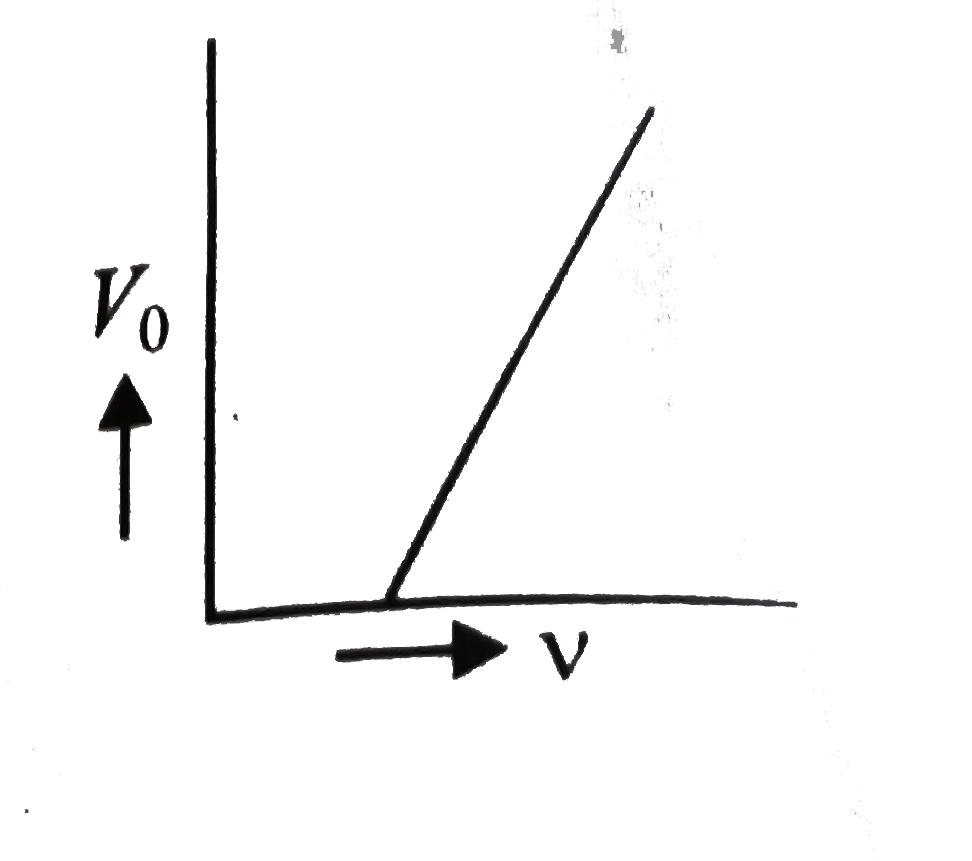
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
`(1)/(2) mv_(max)^(2) = h(v) - h(v_(n)) = hv [(1)/(lambda) -0 (1)/(lambda_(n))]`
Where `v_(n)` and `lambda_(0)` are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if `V_(0)` is the stopping potential `eV_(0) = h(v- v_(0))`
The stopping potential as a function on electron frtequency is plotted for two photoelectric surface A abd B The graph show that the work function of A is

View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
`(1)/(2) mv_(max)^(2) = h(v) - h(v_(n)) = hv [(1)/(lambda) -0 (1)/(lambda_(n))]`
Where `v_(n)` and `lambda_(0)` are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if `V_(0)` is the stopping potential `eV_(0) = h(v- v_(0))`
Whaich of the following is the graph between the frequency (V) of the incident radiation and the stopping potential (v) ?
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
`(1)/(2) mv_(max)^(2) = h(v) - h(v_(n)) = hv [(1)/(lambda) -0 (1)/(lambda_(n))]`
Where `v_(n)` and `lambda_(0)` are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if `V_(0)` is the stopping potential `eV_(0) = h(v- v_(0))`
The folloeing figure indicates the energy livels of a certain atom .When the system moves from `2E` level to E lvel a photon of wavelength `lambda` is emitted .The wavelength of the photon produced during the transition from level `4E//3` to level E is

View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
`(1)/(2) mv_(max)^(2) = h(v) - h(v_(n)) = hv [(1)/(lambda) -0 (1)/(lambda_(n))]`
Where `v_(n)` and `lambda_(0)` are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if `V_(0)` is the stopping potential `eV_(0) = h(v- v_(0))`
Which graph is correct ?
View SolutionIt is tempting to think that all possible transition are permissible and that an atomic spectrum arises from the transition of an electron from any initial orbital to any other orbital .However this is not so because a photon a photon has as intrinsic spin angular momentum of `sqrt(2) h// 2pi` corresponding to `S = 1` although it has no charge and no rest mass
On the other hand , an electron has got two type of angular momentum: orbital angular momentum
`L = [sqrt(l(l+1))] h//2pi`,and spin angular momentum `L_(1) = sqrt(s(s + 1)) h//2pi` arising from orbital motion and spin motion of the electron during any electronic transition must compensate for the angular momentum carried away by the photon .To satisfy this condition the different between the azimuthal quantum number of the orbital within which the transition take place must differ by 1.thus, an electron in a d-orbital `(l = 2)` cannot make a transition into as s-orbital `(l = 0)`because the photon cannot carry away enough angular momentum
The maximum orbital angular momentum of an electron with `n = 5` is
View SolutionIt is teming to think that all possible transituion are permissible and that an atomic spectrum series from the transition of an electron from any intial orbital to any other .However this is not so because a photon a photon has as intrinsic spin angular momentum of `sqrt(2) h// 2pi` corresponding to `S = 1` although it has no charge and no rest mass
On the other hand , an electron has got two typwe of agular momentum orbit angular momentum
`L = [sqrt(l(l+1))] h//2pi`,and spin angular momentum `L_(1) = sqrt(s(s + 1)) h//2pi` arising from orbital motion and spin motion of the electronn during any electton transition must compentum for the angular momentum carried away by the photon .To salary this condition the different between the azisition quantum number of teh orbital witjhin which the transition `(l = 2)` cannot make a transition into as x-orbital `(l = 0)`because the photon cannot carry away enough angular momentum
The maximum orbital angular momentum of an electon with `n = 5` is
View SolutionThe energy of state `s_(1)` in units of the hydrogen atom ground state energy in
View SolutionThe hydrogen -like species `Li^(2+)` is in a spherically symmetric state `S_(1)` with one node. Upon absorbing light , the ion undergoes transition to a state `S_(2)`. The state `S_(2)` has one radial node and its energy is equal is to the ground state energy of the hydrogen atom.
The orbital angular momentum quantum number of the state `S_(2)` is
View Solution
Exercises Linked Comprehension questions and complete solutions for chapter ATOMIC STRUCTURE of CENGAGE CHEMISTRY (ENGLISH) of Class 11
All Exercises from CENGAGE CHEMISTRY Class 11 CHEMISTRY ATOMIC STRUCTURE
- Archives (Linked Comprehension
- Archives Fill In The Balnks
- Archives Integer
- Archives Multiple Correct
- Archives Single Correct
- Archives Subjective
- Archives True And False
- Concept Applicationexercise (4.1)
- Concept Applicationexercise(4.2)
- Concept Applicationexercise(4.3)
- Exercises (Subjective)
- Exercises Assertion And Reason
- Exercises Fill In The Balnks
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises True And False
- Solved Example