Complete Solutions to Comprehension of chapter ARCHIVES 2 VOLUME 6 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ARCHIVES 2 VOLUME 6 |
| CENGAGE PHYSICS | Comprehension |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
Waves `y_(1) = Acos(0.5pix - 100pit)` and `y_(2)=Acos(0.46pix - 92pit)` are travelling along x-axis. (Here `x` is in `m` and `t` is in second)
(1) Find the number of times intensity is maximum in time interval of `1 sec`.11:32View SolutionWaves `y_(1) = Acos(0.5pix - 100pit)` and `y_(2)=Acos(0.46pix - 92pit)` are travelling along x-axis. (Here `x` is in `m` and `t` is in second)
(2) The wave velocity of louder sound is11:32View SolutionWaves `y_(1) = Acos(0.5pix - 100pit)` and `y_(2)=Acos(0.46pix - 92pit)` are travelling along x-axis. (Here `x` is in `m` and `t` is in second)
(3) The number of times `y_(1) + y_(2) = 0` at `x = 0` in `1sec` is11:32View SolutionTwo trains `A and B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahead of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. The spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. The speed of sound in still air is `340 m//s`.
(4) The speed of sound of the whistle is10:09View SolutionTwo trains `A and B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahead of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. the spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. the speed of sound in still air is `340 m//s`.
(5) The distribution of the sound intensity of the whistle as observed by the passengers in train `A` is best represented by10:09View SolutionTwo trains `A and B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahead of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. the spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. the speed of sound in still air is `340 m//s`.
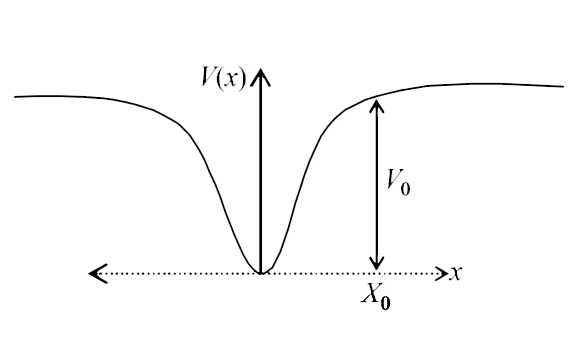
The spread of frequency as observed by the passenger in train `B` is10:09View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
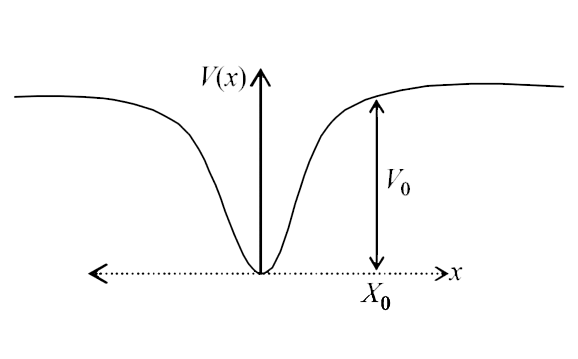
If total energy of the particle is E, it will perform perildic motion only if.04:24View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
 .
.
For periodic motion of small amplitude A,the time period (T) of thes particle is proportional to.02:33View SolutionWhen a particle of mass m moves on the x-axis in a potential of the form `V(x) =kx^(2)` it performs simple harmonic motion. The correspondubing time period is proprtional to `sqrtm/h`, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of `x=0` in a way different from `kx^(2)` and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is `V(x)=ax^(4)(agt0)` for |x| neat the origin and becomes a constant equal to `V_(0)` for |x|impliesX_(0)` (see figure).
 .
.
The acceleration of this partile for `|x|gtX_(0)` is
(a) proprtional to `V_(0)`
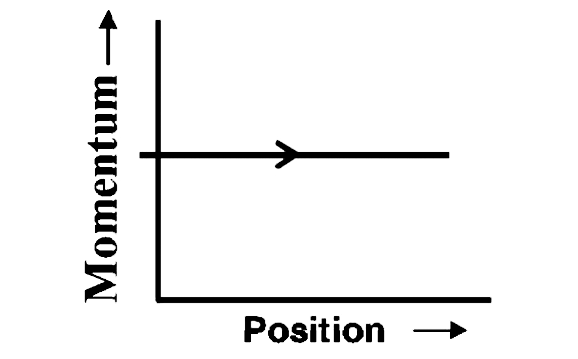
(b) proportional to.01:49View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is `x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
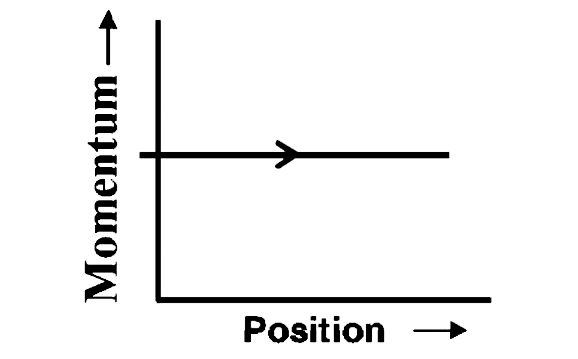
The phace diagram for a ball thrown vertically up from ground is.03:16View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is `x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
The plase space deagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial condetions, and E_(1) and E_(2) the total mechanical energies respectivey.
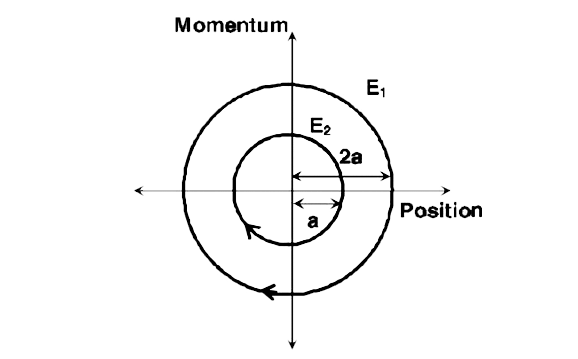 .02:22View Solution
.02:22View SolutionPhase space deagrams are useful tools
 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is `x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
Consider the spring-mass system, with mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is.
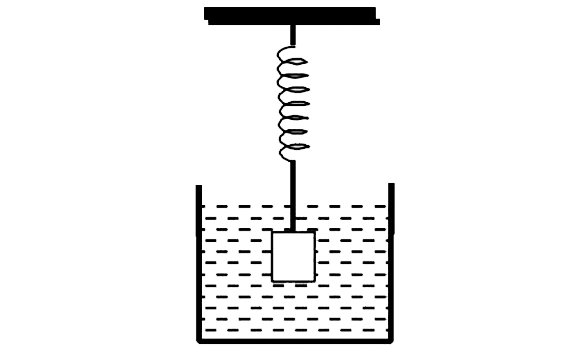 .03:56View Solution
.03:56View Solution
Comprehension questions and complete solutions for chapter ARCHIVES 2 VOLUME 6 of CENGAGE PHYSICS (HINGLISH) of Class 11
