Complete Solutions to LC_TYPE of chapter MISCELLANEOUS VOLUME 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MISCELLANEOUS VOLUME 2 |
| CENGAGE PHYSICS | LC_TYPE |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
A man standing on a inclined plain observes rain is falling verticaly. When he starts moving down the inclined plain with velocity `v=6m//s` observes rain hitting him horizontally.

The actual velocity of rain is
View SolutionA man standing on a inclined plain observes rain is falling vertically. When he starts moving down the inclined plain with velocity `v=6m//s` observes rain hitting him horizontally.

The velocity of rain with respect to the man when he is moving down is
View SolutionA straight rigid rod of mass `M` and length `L` lies on a smooth horizontal table. Taking the co-ordinate axes as shown in the figure and assuming an average force `ltFgt` acting for a small time interval `(/_\t)`, at the end `A`, making an angle `30^@` with the `X`-axis, Based on the above passege, answer the following questions.
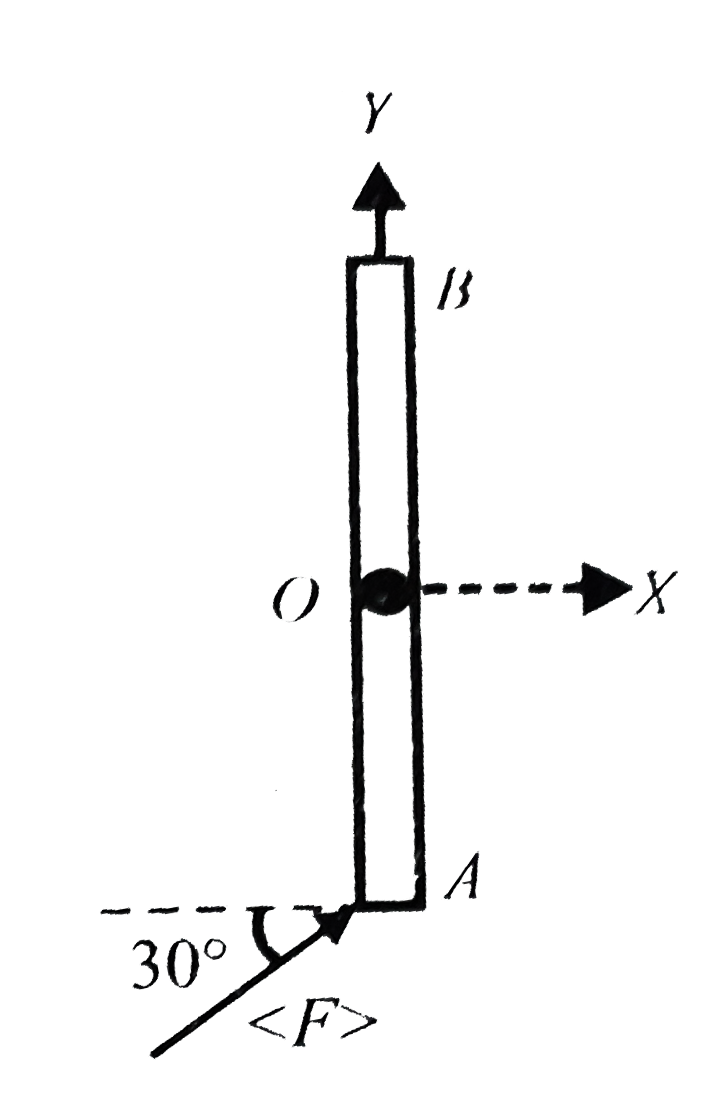
The angular impulse, due to the force about `O`, is
View SolutionA straight rigid rod of mass `M` and length `L` lies on a smooth horizontal table. Taking the co-ordinate axes as shown in the figure and assuming an average force `ltFgt` acting for a small time interval `(/_\t)`, at the end `A`, making an angle `30^@` with the `X`-axis, Based on the above passege, answer the following questions.
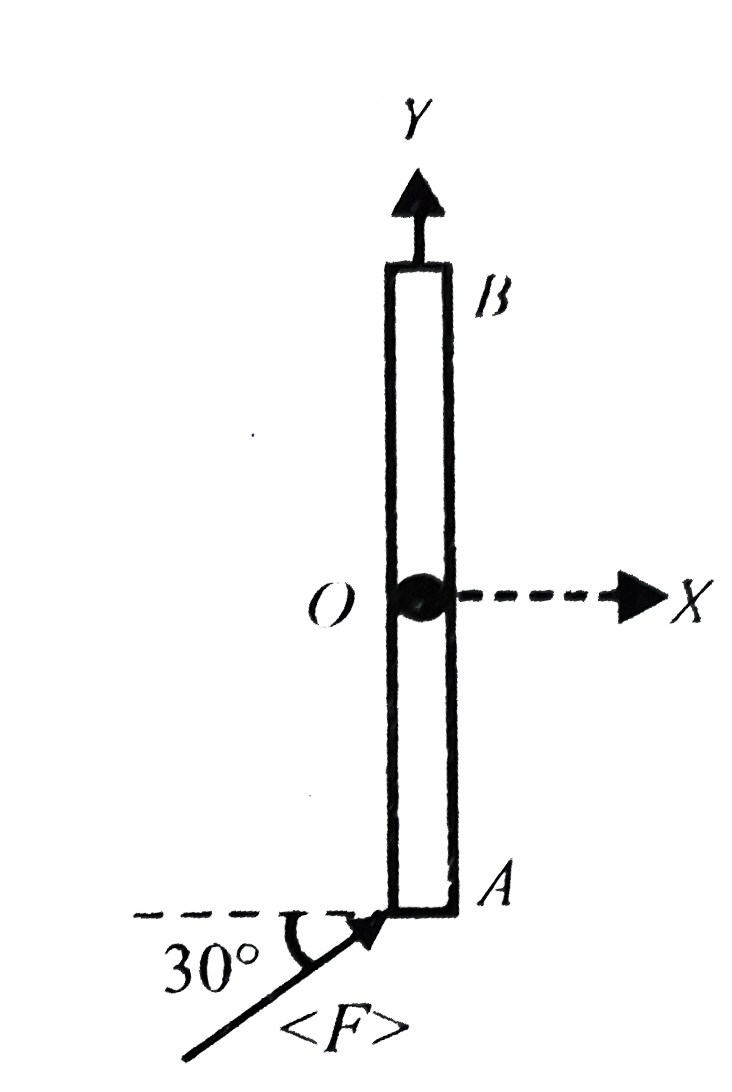
Angular velocity of rod about `O` is
View SolutionA straight rigid rod of mass `M` and length `L` lies on a smooth horizontal table. Taking the co-ordinate axes as shown in the figure and assuming an average force `ltFgt` acting for a small time interval `(/_\t)`, at the end `A`, making an angle `30^@` with the `X`-axis, Based on the above passege, answer the following questions.
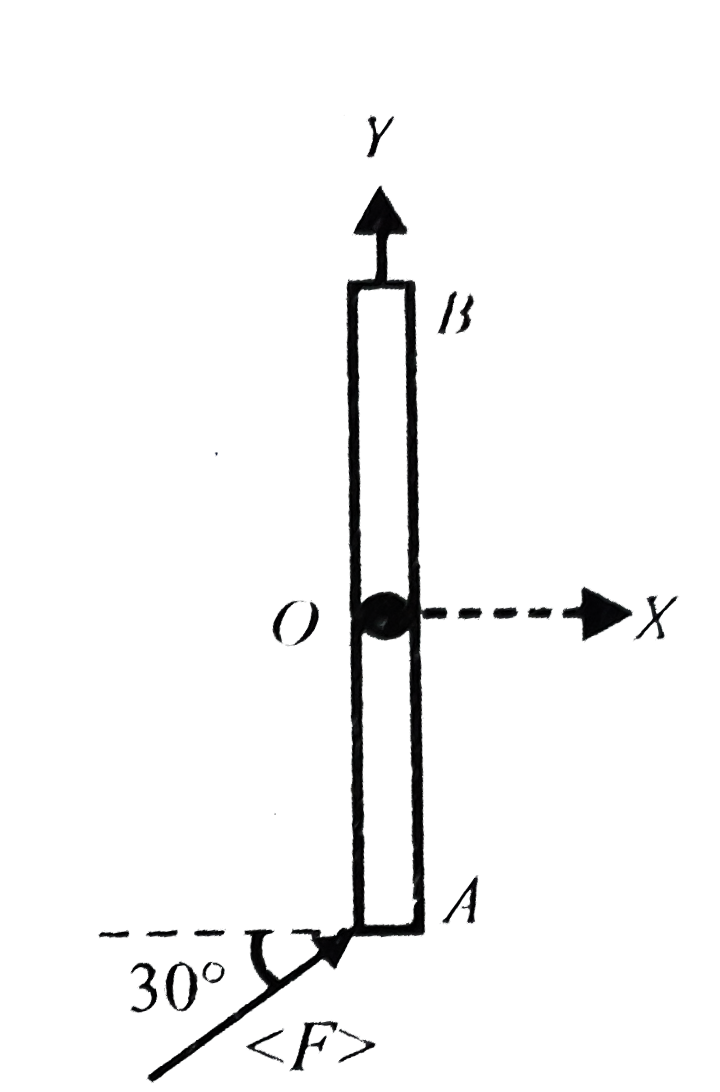
Linear velocity of the `CM` of rod is
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its `KE` is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
Velocity of the planet is minimum at
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its `KE` is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
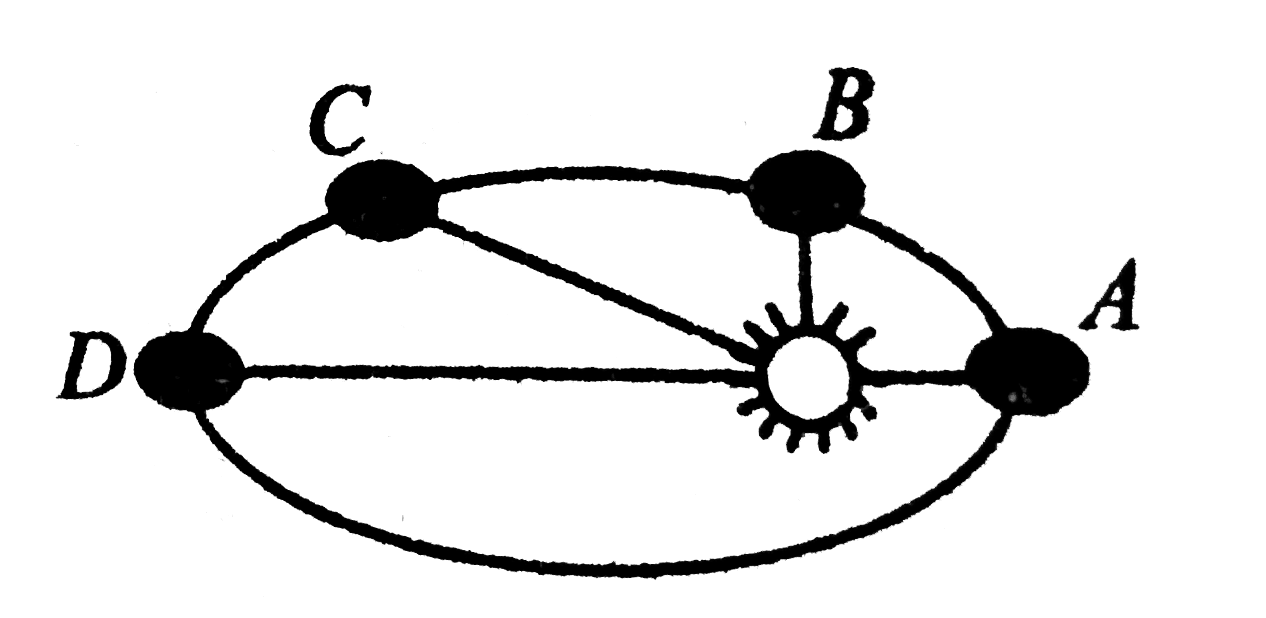
Net torque on the planet is
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its `KE` is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
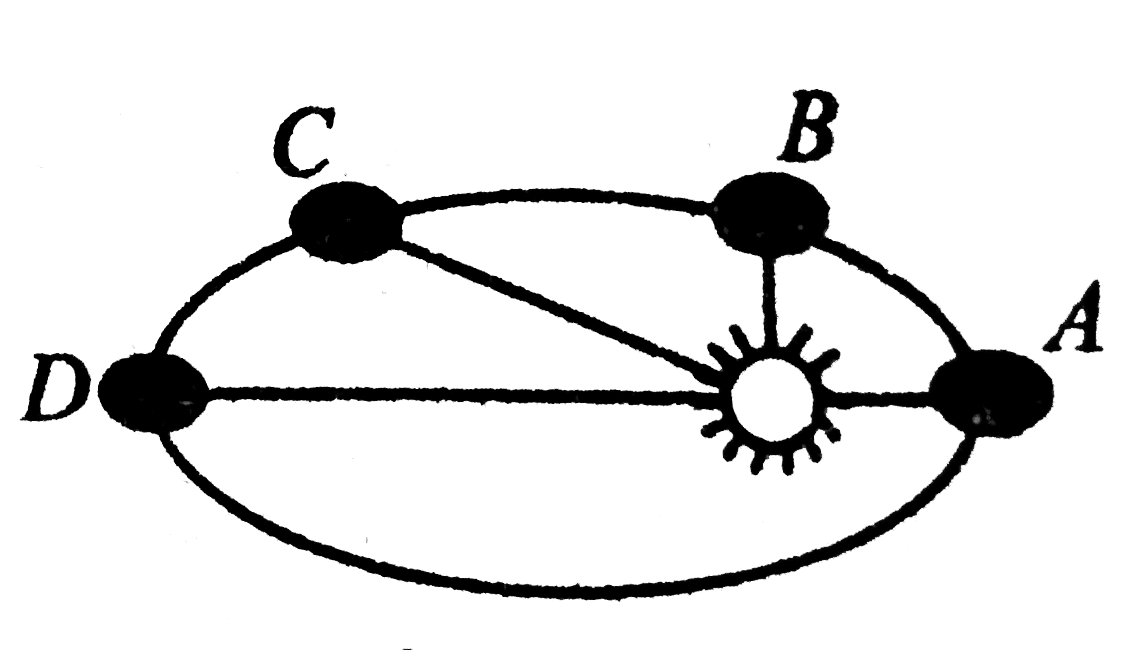
Linear momentum of the planet is
View SolutionA train is moving with a constant speed of `10m//s` in a circle of radius `16/pi`m. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed `10m//s` relative to train towards negative x-axis at an angle of `37^@` with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g `= 10 m//s^2, sin 37^@ = 3/5`
View SolutionA train is moving with a constant speed of `10m//s` in a circle of radius `16/pi`m. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed `10m//s` relative to train towards negative x-axis at an angle of `37^@` with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g `= 10 m//s^2, sin 37^@ = 3/5`

View SolutionA train is moving with a constant speed of `10m//s` in a circle of radius `16/pi`m. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed `10m//s` relative to train towards negative x-axis at an angle of `37^@` with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g `= 10 m//s^2, sin 37^@ = 3/5`

View SolutionA model rocket rests on a frictionless horizontal surface and is joined by a string of length `l` to a fixed point so that the rocket moves in a horizontal circular path of radius `l`. The string will break if its tensiion exceeds a value `T`. The rocket engine provides a thrust `F` of constant magnitude along the rocket's direction of motion. the rocket has a mass `m` that does not change with time. Answer the following questions based on the above passage.
Starting from rest at `t=0` at what later time `t_(1)` is the rocket travelling so fast that the string breaks. Ignnore any air resistance.
View SolutionA model rocket rests on a frictionless horizontal surface and is joined by a string of length `l` to a fixed point so that the rocket moves in a horizontal circular path of radius `l`. The string will break if its tensiion exceeds a value `T`. The rocket engine provides a thrust `F` of constant magnitude along the rocket's direction of motion. the rocket has a mass `m` that does not change with time. Answer the following questions based on the above passage.
What was the magnitude of instantaneous net acceleration at time `t_(1)//2`? Obtain answer in terms of `F, T` and `m`.
View SolutionA model rocket rests on a frictionless horizontal surface and is joined by a string of length `l` to a fixed point so that the rocket moves in a horizontal circular path of radius `l`. The string will break if its tensiion exceeds a value `T`. The rocket engine provides a thrust `F` of constant magnitude along the rocket's direction of motion. the rocket has a mass `m` that does not change with time. Answer the following questions based on the above passage.
What distance does the rocket travel between the time `t_(1)` when the string breaks and the time `2t_(1)`? The rocket engine continues of operate after the string breaks.
View SolutionTwo ropes are puling a large ship at rest of mass `1xx106kg` into harbour. Rope A exerts a force of `40,000N` and rope `B` exerts a force of `30,000N`.
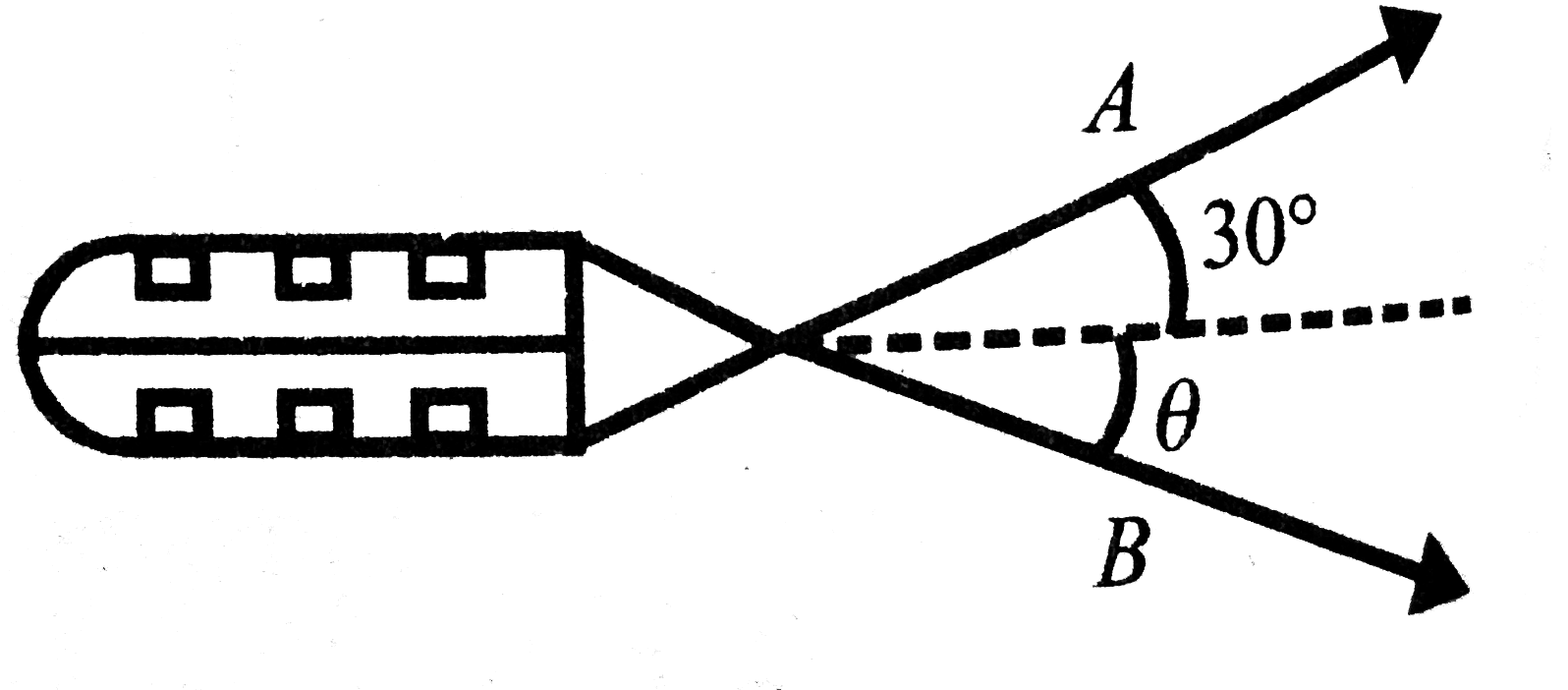
The angle `theta` if the slip is to move directly forward is
View SolutionTwo ropes are puling a large ship at rest of mass `1xx106kg` into harbour. Rope A exerts a force of `40,000N` and rope B exerts a force of `30,000N`.

If the acceleration of the ship is `0.03ms^(-2)`, the magnitude of the resistive forces on the ship is
View SolutionTwo ropes are puling a large ship at rest of mass `1xx106kg` into harbour. Rope A exerts a force of `40,000N` and rope B exerts a force of `30,000N`.
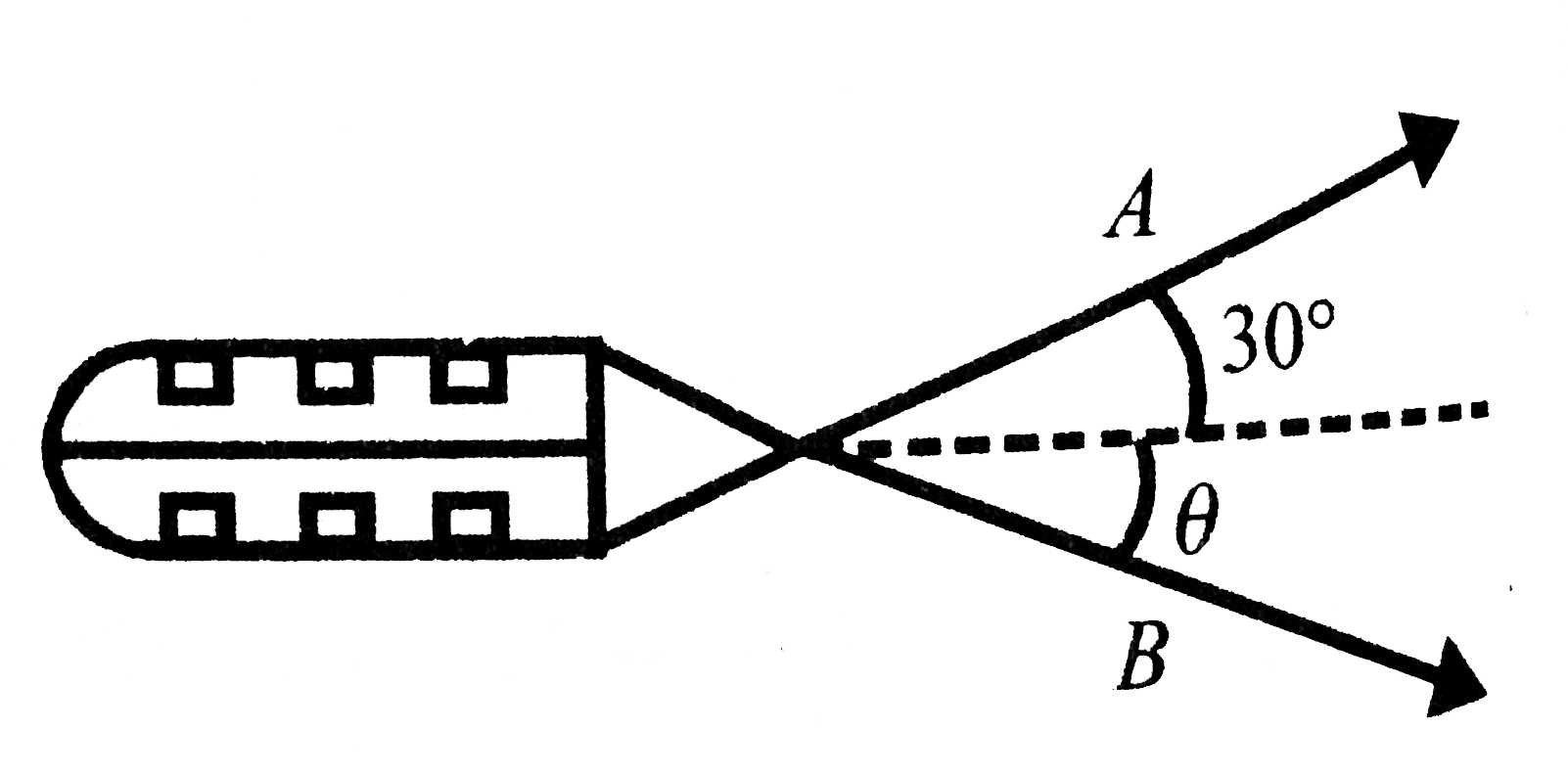
The time for the ship to travel `6m` to the the dock is
View SolutionIn the given figure `F=10N, R=1m`, mass of the body is `2kg` and moment of inertia of the body about an axis passing through `O` and perpendicular to the plane of the body is `4kgm^(2)`. `O` is the centre of mass of the body.

If the ground is smooth, what is the total kinetic energy of the body after `2s`?
View SolutionIn the given figure `F=10N, R=1m`, mass of the body is `2kg` and moment of inertia of the body about an axis passing through `O` and perpendicular to the plane of the body is `4kgm^(2)`. `O` is the centre of mass of the body.

If the ground is sufficiently rough to ensure rolling, what is the kinetic energy of the body now in the given time interval of `2s`?
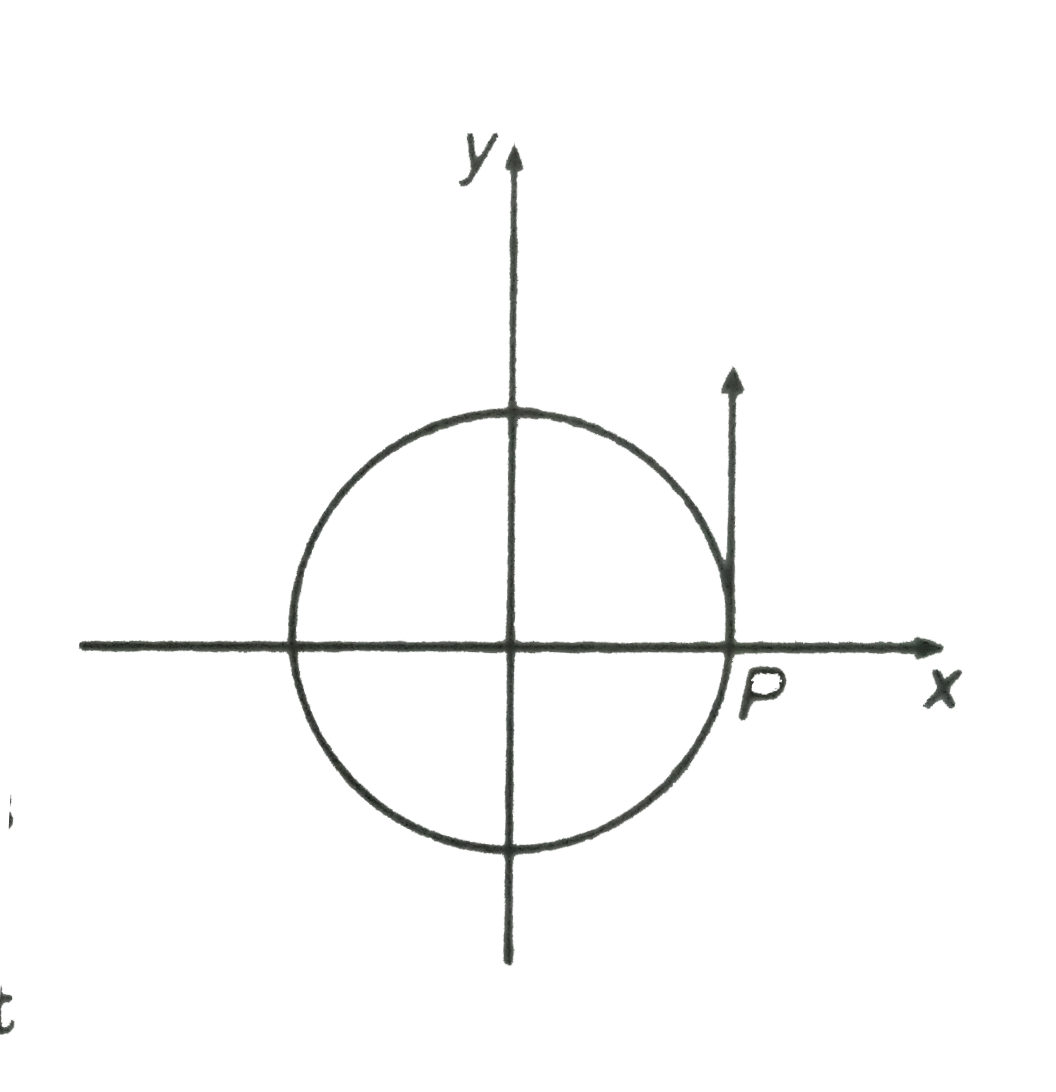
View SolutionA disc having radius `R` is rolling without slipping on a horizontal (`x-z`) plane. Centre of the disc has a velocity `v` and acceleration `a` as shown.

Speed of point `P` having coordinates `(x,y)` is
View SolutionA disc having radius `R` is rolling without slipping on a horizontal (`x-z`) plane. Centre of the disc has a velocity ` v` and acceleration `a` as shown.
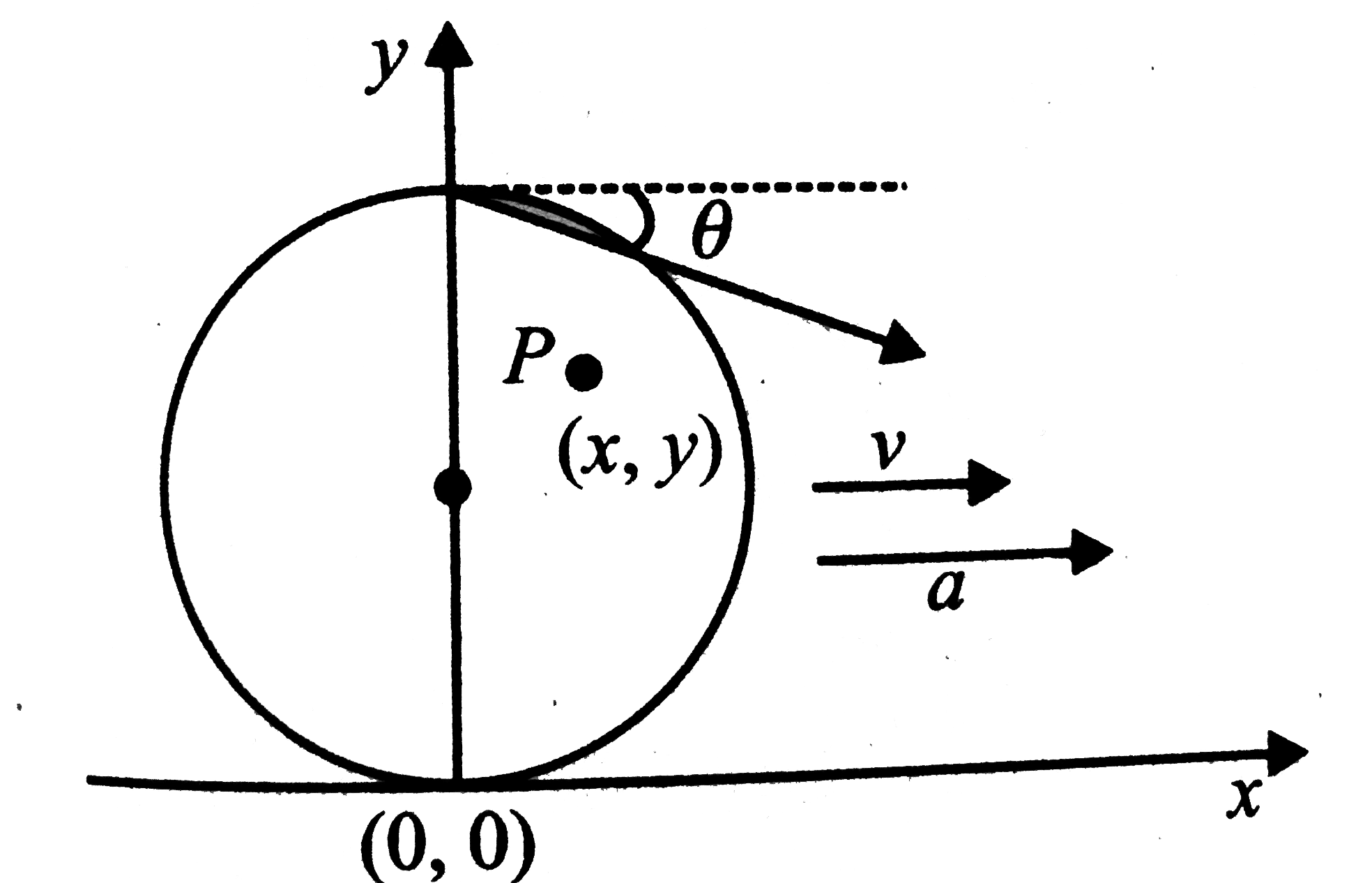
If `v=sqrt(2aR)` the angle `rho` between acceleration of the top most point and the horizontal is
View SolutionA cylindrical container of length `L` is full to the brim with a liquid which has mass density `rho`.it is placed on a weight -scale, the scale reading is `W`. A light ball of volume `V` and mass `m` which wold float on the liquid, if allowed to do so, is pushed gently downand held beneath the surface of the liquid with a rigid rod of negligible volume as shwon on the left.
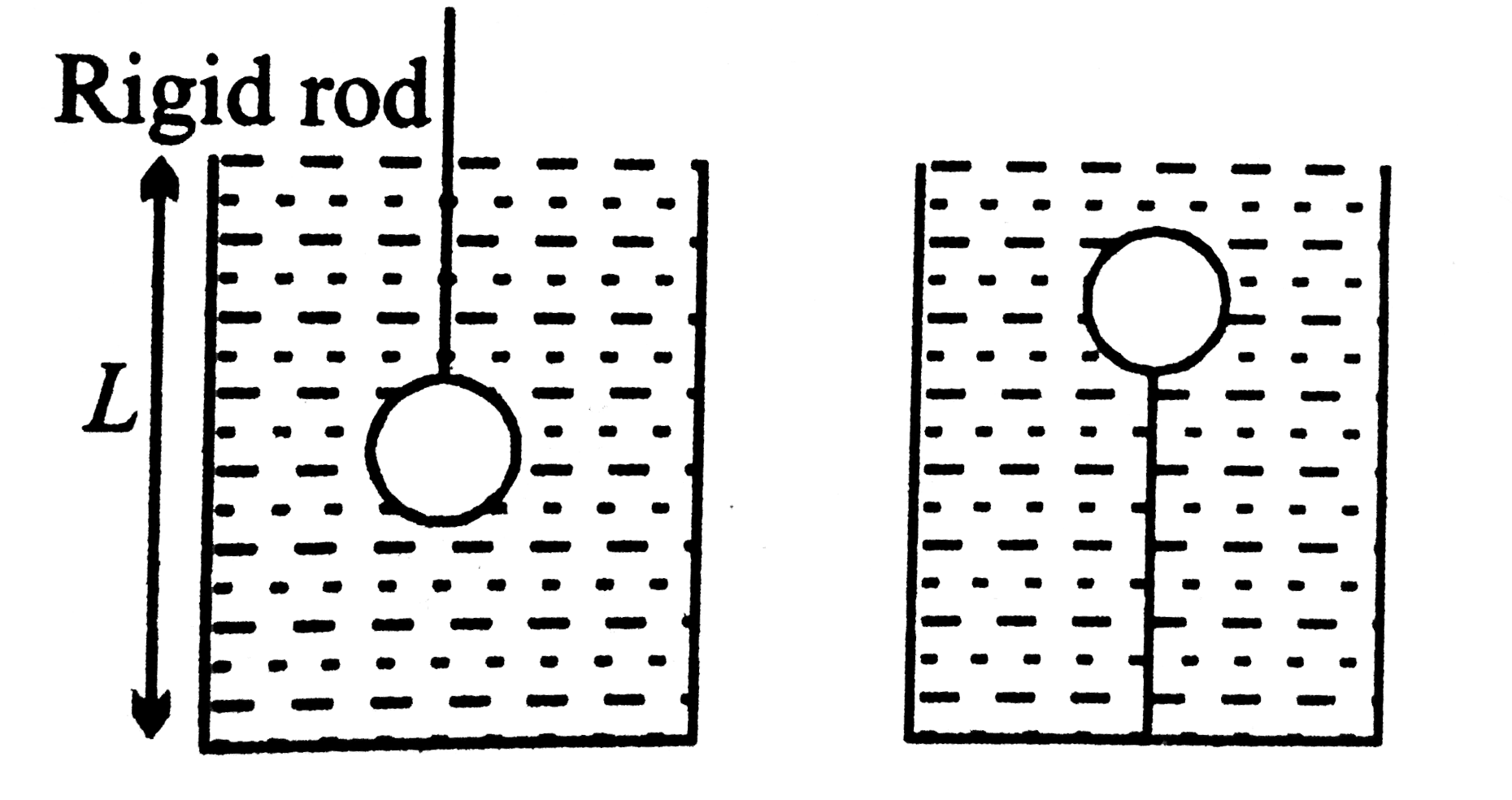
What is the mass `M` of the liquid which overflowed while the ball was being pushed into the liquid?
View SolutionA cylindrical container of length `L` is full to the brim with a liquid which has mass density `rho`.it is placed on a weight -scale, the scale reading is `W`. A light ball of volume `V` and mass `m` which wold float on the liquid, if allowed to do so, is pushed gently downand held beneath the surface of the liquid with a rigid rod of negligible volume as shwon on the left.
What is the reading of the scale when the ball is fully immersed?
If instead of being pushed down by the rod, the ball is held in place by a thin string attached to the bottom of the containier as shown on the right.
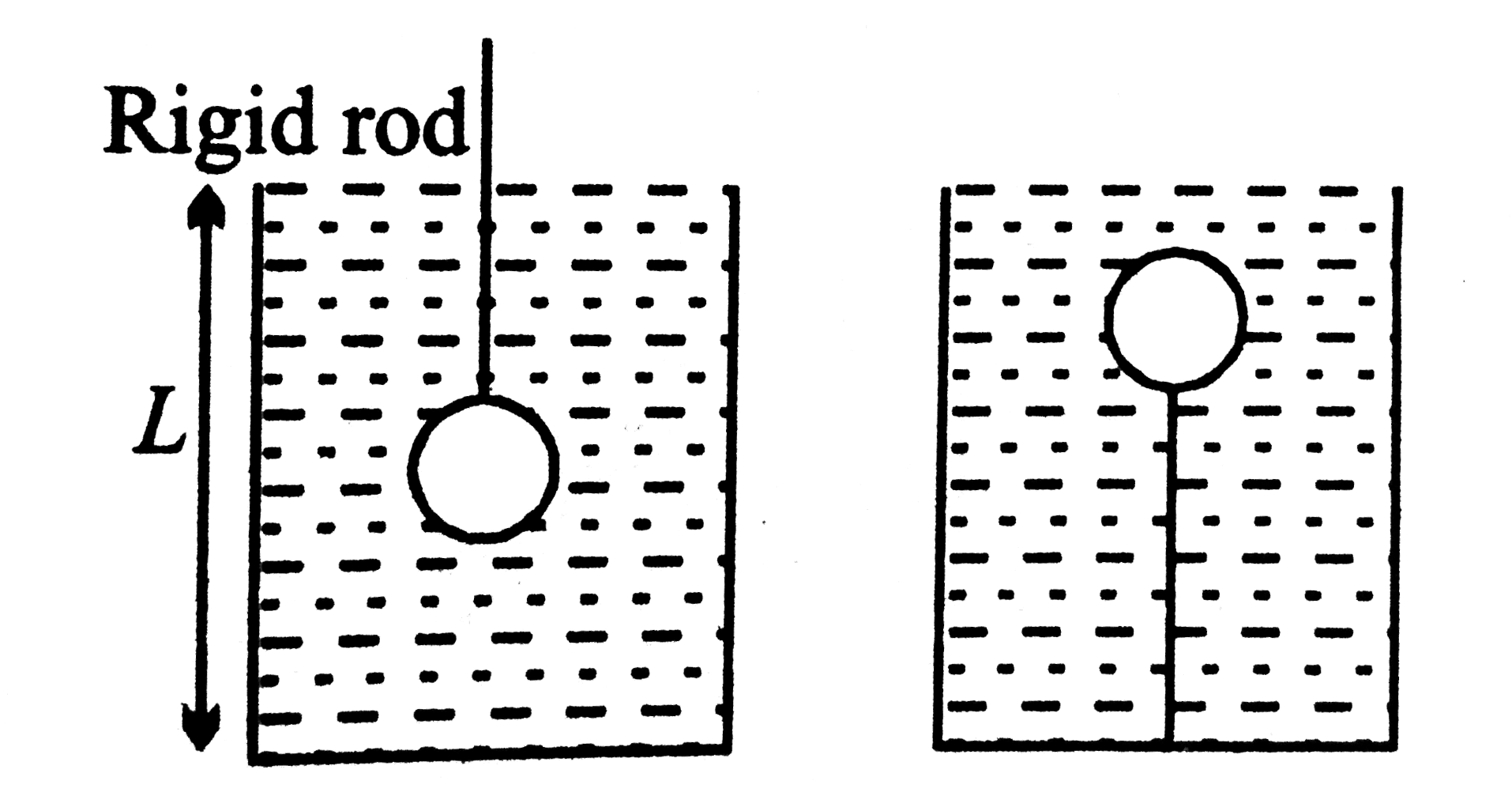
View SolutionA cylindrical container of length `L` is full to the brim with a liquid which has mass density `rho`.it is placed on a weight -scale, the scale reading is `W`. A light ball of volume `V` and mass `m` which woUld float on the liquid, if allowed to do so, is pushed gently downand held beneath the surface of the liquid with a rigid rod of negligible volume as shwon on the left.
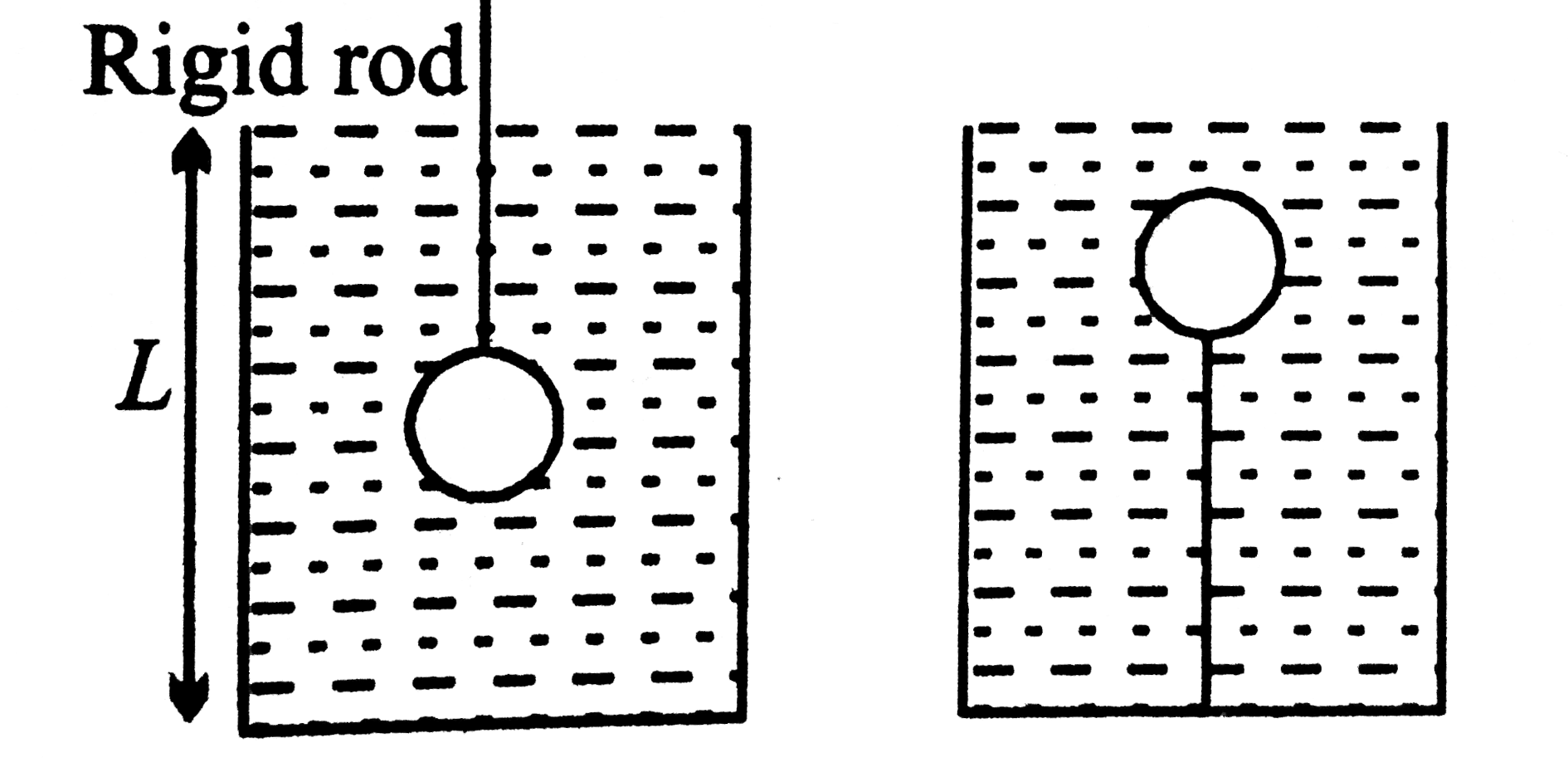
What is the tension `T` in the string?
View SolutionA cylindrical container of length `L` is full to the brim with a liquid which has mass density `rho`.it is placed on a weight -scale, the scale reading is `W`. A light ball of volume `V` and mass `m` which wold float on the liquid, if allowed to do so, is pushed gently downand held beneath the surface of the liquid with a rigid rod of negligible volume as shwon on the left.

What is the reading on the scale?
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the Body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities `d` and `2d`, each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`.
Situation I:
A homogeneous solid cylinder of length `L(LltH//2)`. cross sectional area `A//5` is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght `L//4` in the denser liquid.
The density of the solid is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities `d` and `2d`, each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`.
Situation I:
A homogeneous solid cylinder of length `L(LltH//2)`. cross sectional area `A//5` is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght `L//4` in the denser liquid.
The total pressure at the bottom of the container is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform cross sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities `d` and `2d`, each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`.
Situation II:
A cyliner is removed and the original arrangement is restored.A tiny hole of area `s(slt ltA)` is punched on the veritical sideof the containier at a height `h(hltH//2)`
The initial speed of efflux of the liquid at the hole is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities `d` and `2d`, each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`.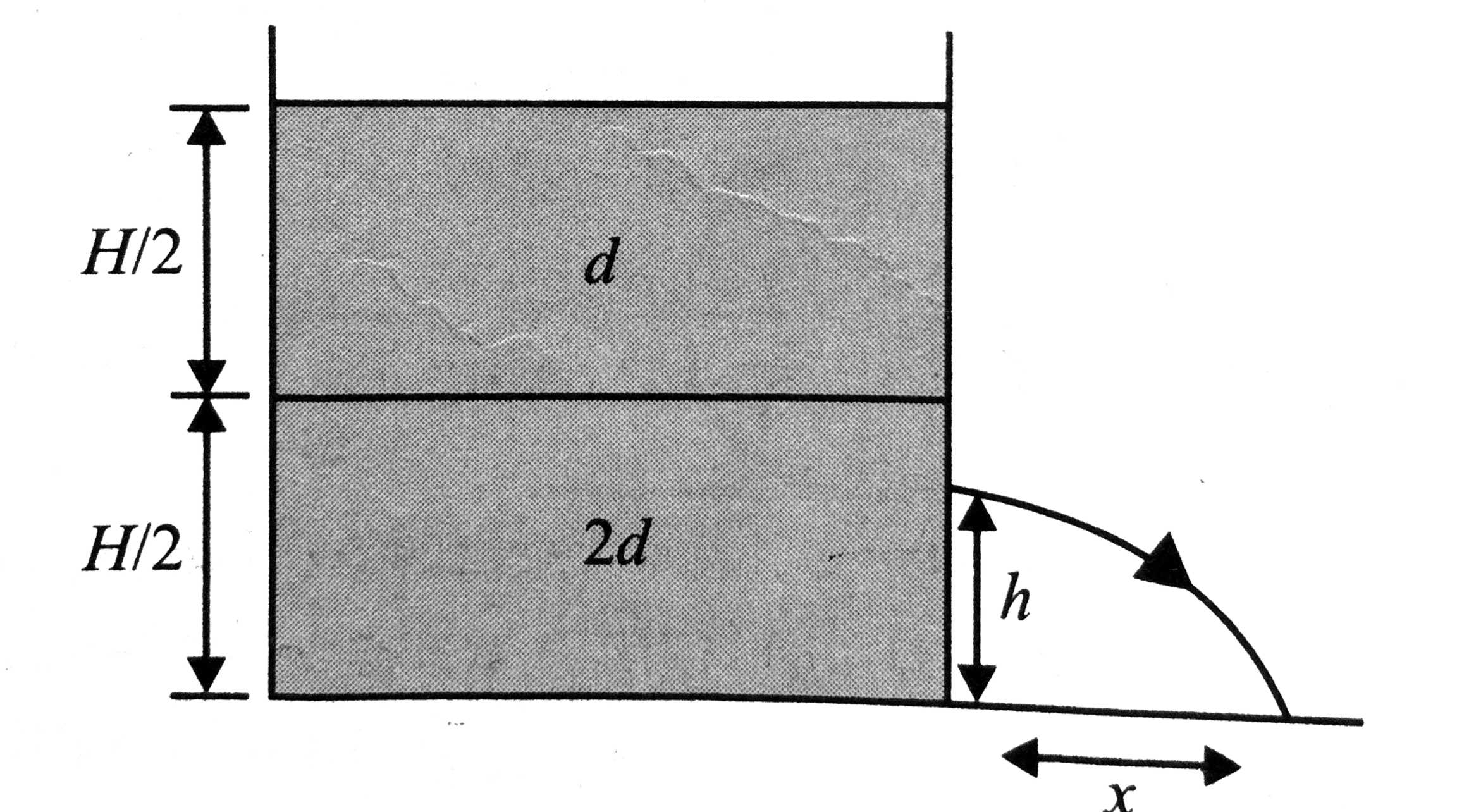
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area `s(slt ltA)` is punched on the veritical sideof the containier at a height `h(hltH//2)`
The horizontal distance `x` travelled by the liquid is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities `d` and `2d`, each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area `s(slt ltA)` is punched on the veritical side of the containier at a height `h(hltH//2)`
The height `h_(m)` at which the hole should be punched so that the liquid travels the maximum distance is
View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the ody immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities `d` and `2d`, each of height `H//2` as shown in the figure. The lower density liquid is open to the atmosphere having pressure `P_(0)`.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area `s(slt ltA)` is punched on the veritical side of the container at a height `h(hltH//2)`
The maximum distance travelled `x_(m)` is
View SolutionA hollow sphere is completely filled with a liquid having a density `rho`. The radius of the sphere is `R`. Now the sphere is puloled with a constant horizontal acceleration of `g` on a horizontal surface. Take centre of sphere as origin of coordinate system as shwon in the figure.

Coordinate of the point having the minimum pressure is
View SolutionA hollow sphere is completely filled with a liquid having a density `rho`. The radius of the sphere is `R`. Now the sphere is puloled with a constant horizontal acceleration of `g` on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Coordinate of the point having the maximum pressure is
View SolutionA hollow sphere is completely filled with a liquid having a density `rho`. The radius of the sphere is `R`. Now the sphere is puloled with a constant horizontal acceleration of `g` on a horizontal surface. Take centre of sphere as origin of coordinate system as shown in the figure.

Consider points `A` and `B` as shown in the figure.
View Solution
LC_TYPE questions and complete solutions for chapter MISCELLANEOUS VOLUME 2 of CENGAGE PHYSICS (HINGLISH) of Class 11