Complete Solutions to EXERCISE of chapter LAWS OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF THERMODYNAMICS |
| CP SINGH | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The first law of thermodynamics incorporates are concept
(i) conservation of energy
(ii) convervation of heat
(iii) conservation of work
(iv) equivalence of heat and work01:14View Solution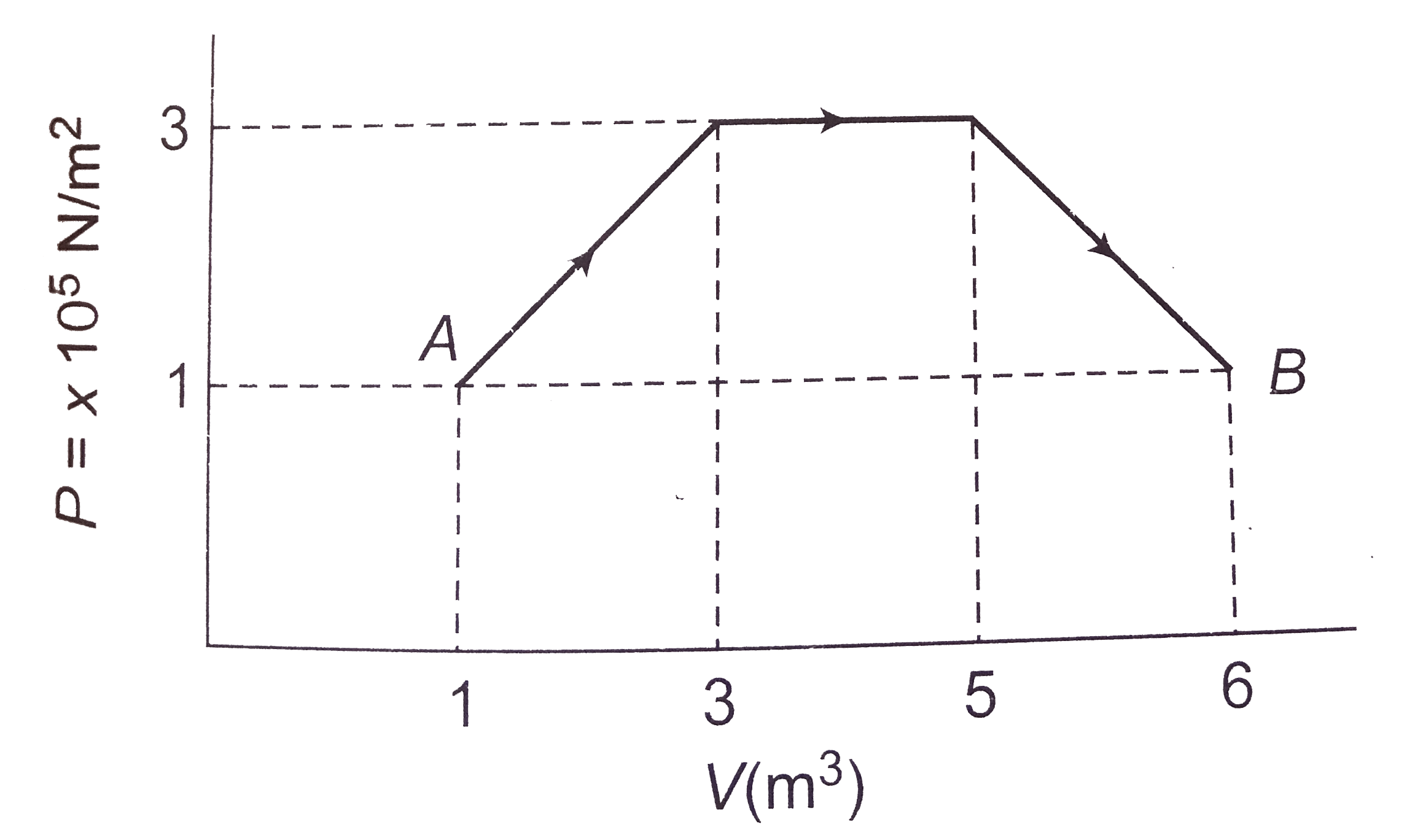
The work done in the process AB is03:45View Solution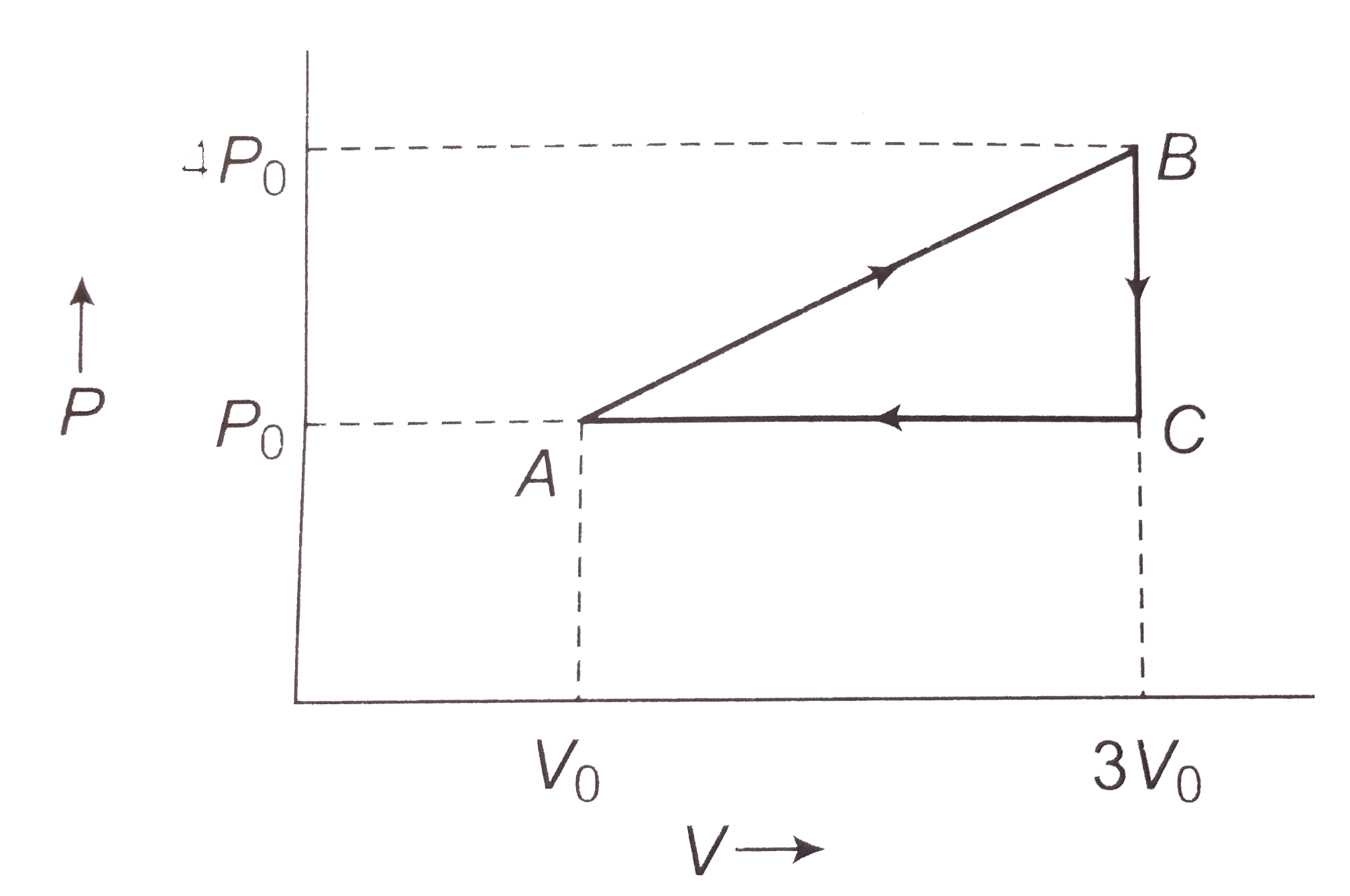
(i) `DeltaW_(AB)=5P_0V_0`
(ii) `DeltaW_(BC)=0`
(iii) `DeltaW_(CA)=-2P_0V_0`
(iv) `DeltaW_(ABCA)=3P_0V_0`04:06View Solution
Consider the process on a system shown in figure. During the process, the work done by the system02:14View SolutionConsider two processes on a system as shown in figure.
The volumes in the initial states are the same in the two processes and the volume in the final states are also the same.Let `DeltaW_(1)` and `DeltaW_(2)` be the work done by the system in the processes `A` and `B` respectively.
 02:49View Solution
02:49View SolutionA system can be taken from the initial state `p_(1),V_(1)` to the final state `p_(2,V_(2)` by two different methods, let `DeltaQ and DeltaW` represent the heat given to the system and the work done by the system. Which of the following must be the same in both the method?
03:22View SolutionIn the figure given two processes `A and B` are shown by which a thermodynamic system goes from initial to final state F. if `DeltaQ_(A)` and `DeltaQ_(B)` are respectively the heats supplied to the systems then
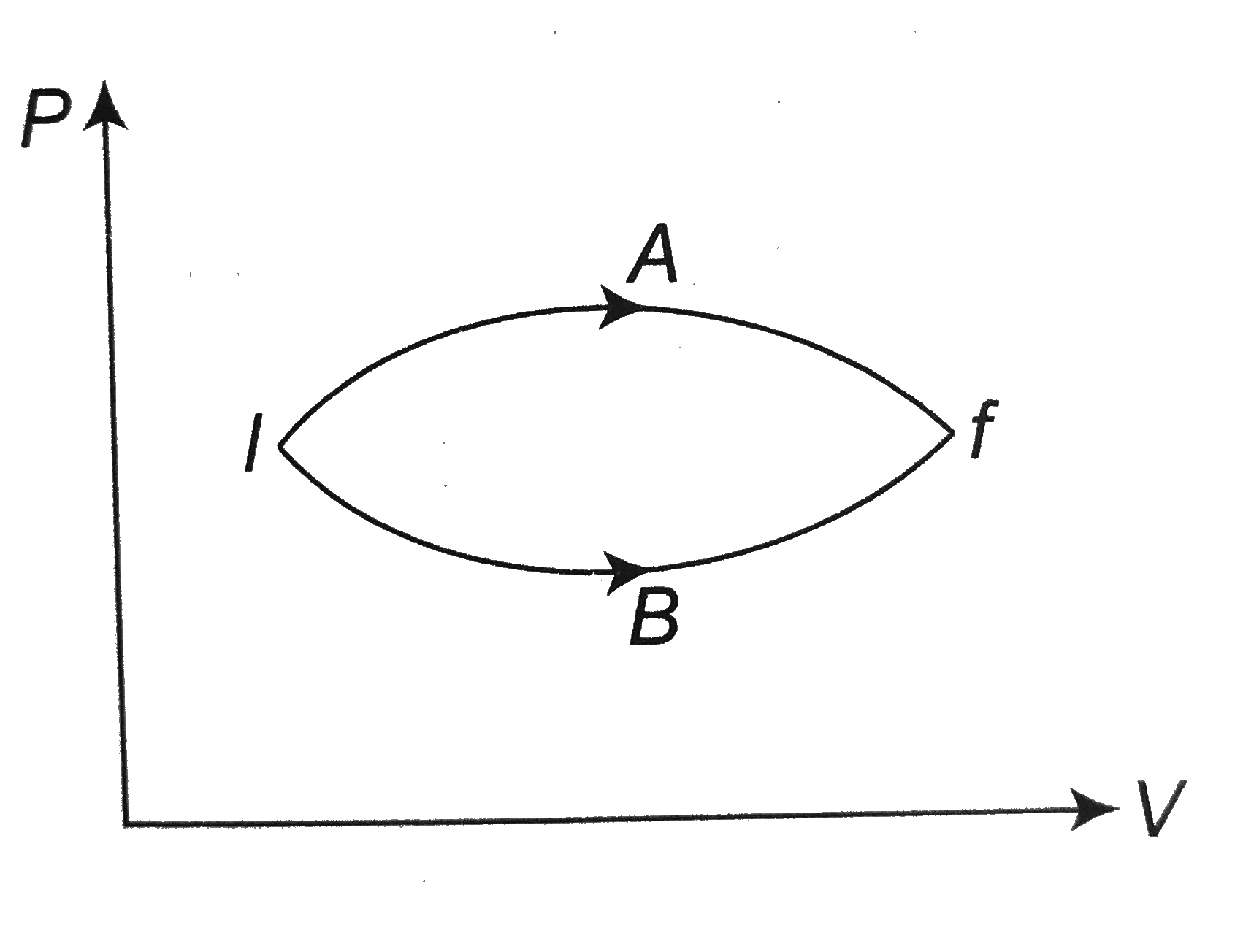 02:11View Solution
02:11View SolutionRefer to figure in previous question, `DeltaU_(1)` and `DeltaU_(2)` be the changes in internal energy of the system in the processes `A` and `B` then
01:04View SolutionRefer to figure `DeltaU_(1)` and `DeltaU_(2)` be the changes in internal energy in the system in process `A+B` and `DeltaW` be the net work done by the system in the process `A+B`,
 03:26View Solution
03:26View SolutionIn a given process on an ideal gas, `dW=0 and dQlt0.` Then for the gas
03:04View SolutionConsider the following two statements.
(A) If heat is added to a system, its temperature must increase.
(B) If positive work is done by a system in a thermodynamic process, its volume must increase.02:11View SolutionIn a process on a system, the initial pressure and volume are equal to the final pressure and volume
(i) The initial temperature must be equal to the final temperature
(ii) The initial internal energy must be equal to the final internal energy
(iii) The net heat given to the system in the process must be zero.
(iv) The net work done by the sytem in the process must be zero.03:28View SolutionThe pressure `p` and volume `V` of an ideal gas both increase in a process.
02:12View SolutionThe state of a thermodynamic system is represented by
01:41View SolutionWhich of the following is not a thermodynamical function
01:43View SolutionIf Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed cycle process, then
01:07View SolutionFor free expansion of the gas, which of the following is true?
01:53View SolutionA system is given 300 calories of heat and it does 600 joules of work. How much does the internal energy of the system change in this process `(J=4.18 "joules"//cal)`
02:22View SolutionIn thermodynamic process, pressure of a fixed mass of a gas is changes in such a manner that the gas molecules gives out 20 J of heat and 10 J of work is done in the gas. If the initial internal energy of the gas was 40 J, then the final internal energy will be
02:24View SolutionA perfect gas goes from a state A to another state B by absorbing 8 × 105 J of heat and doing 6.5 × 105 J of external work. It is now transferred between the same two states in another process in which it absorbs 105 J of heat. In the second process
00:58View SolutionAn ideal gas goes from the state `i` to the state `f` as shown in the figure.The work done by the gas during the process
 01:37View Solution
01:37View SolutionA thermodynamic system is taken through the cycle `ABCD` as shown in the figure. Heat rejected by the gas during the cycle is
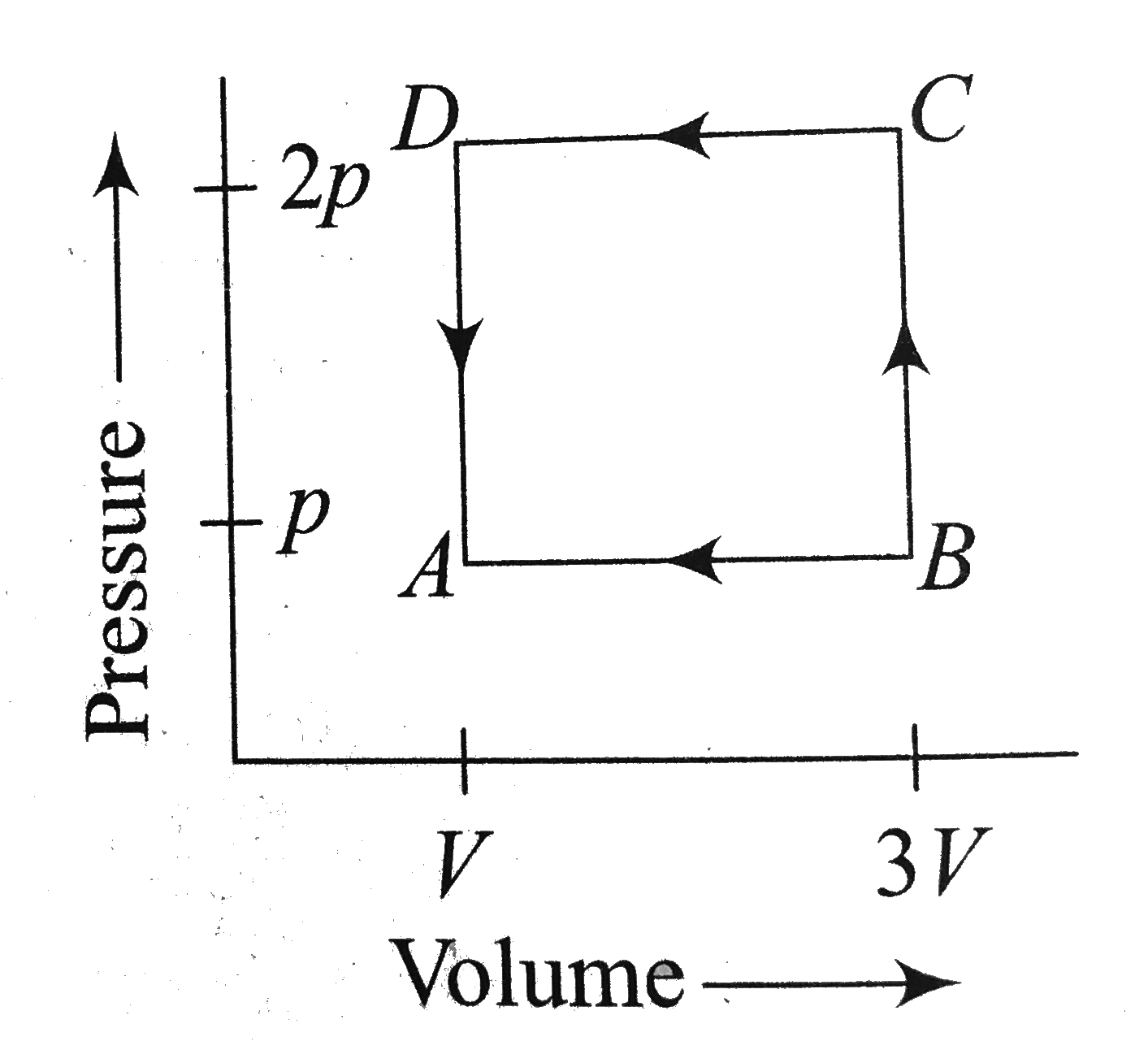 02:11View Solution
02:11View Solution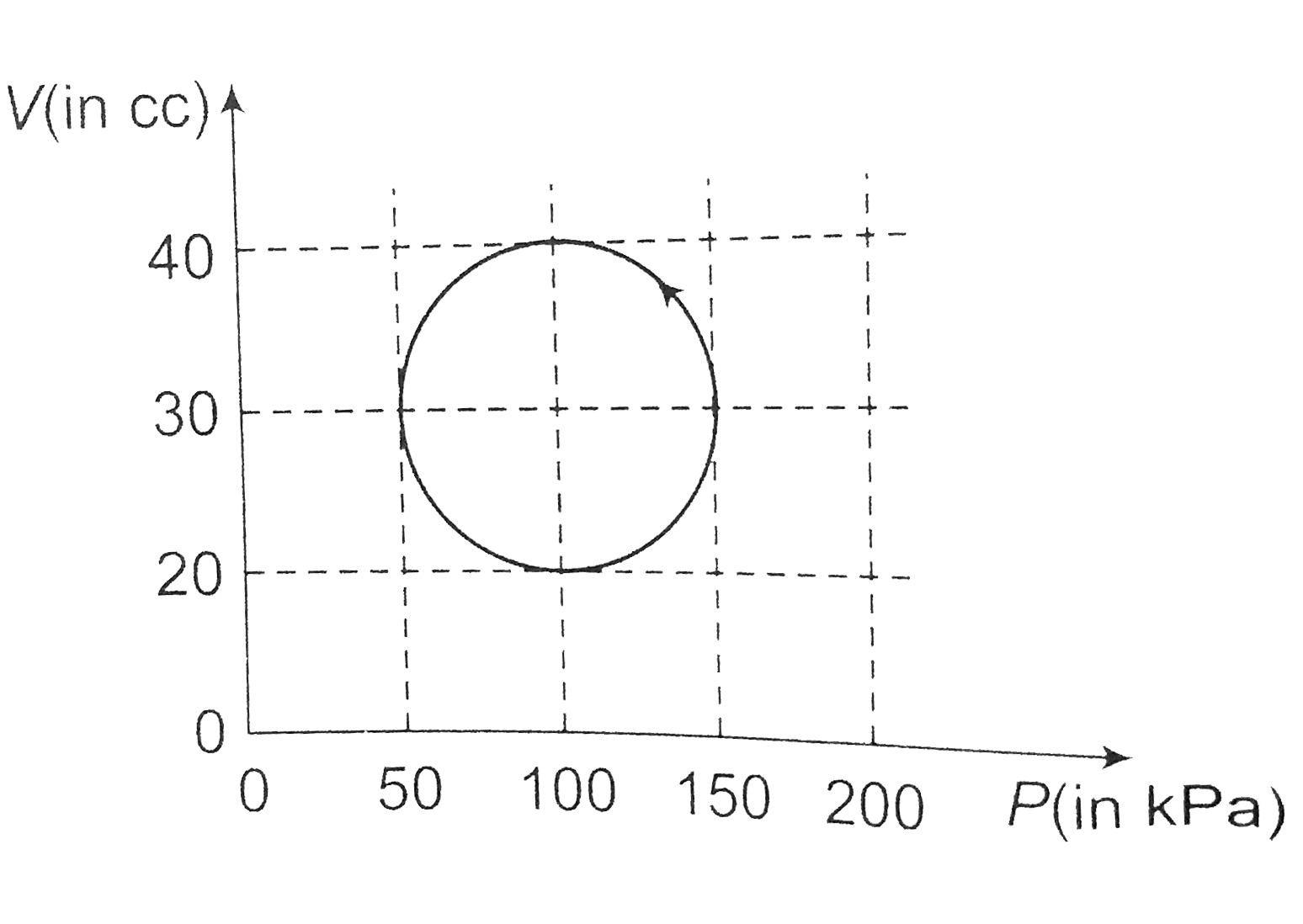
A system is taken through a cyclic process represented by a circle as shown in the figure. The heat absorbed by the system is04:41View SolutionA thermodynamic process is shown in Fig. The pressures and volumes corresponding to some points in the figure are : `P_(A) = 3 xx 10^(4) Pa, P_(B) = 8 xx 10^(4) Pa` and `V_(A) = 2 xx 10^(-3) m^(3) , V_(D) = 5 xx 10^(-3) m`.
In process `AB, 600 J` of heat is added to the system and in process `BC, 200 J` of heat is added to the system. The change in internal energy of the energy of the process `AC` would be.
 02:44View Solution
02:44View SolutionWhen a system is taken from state f along path `iaf, Q = 50 J` and `W = 20 J`. Along path `ibf, Q = 35 J`. If `W = -13 J` for the curved return path `f I, Q` for this path is
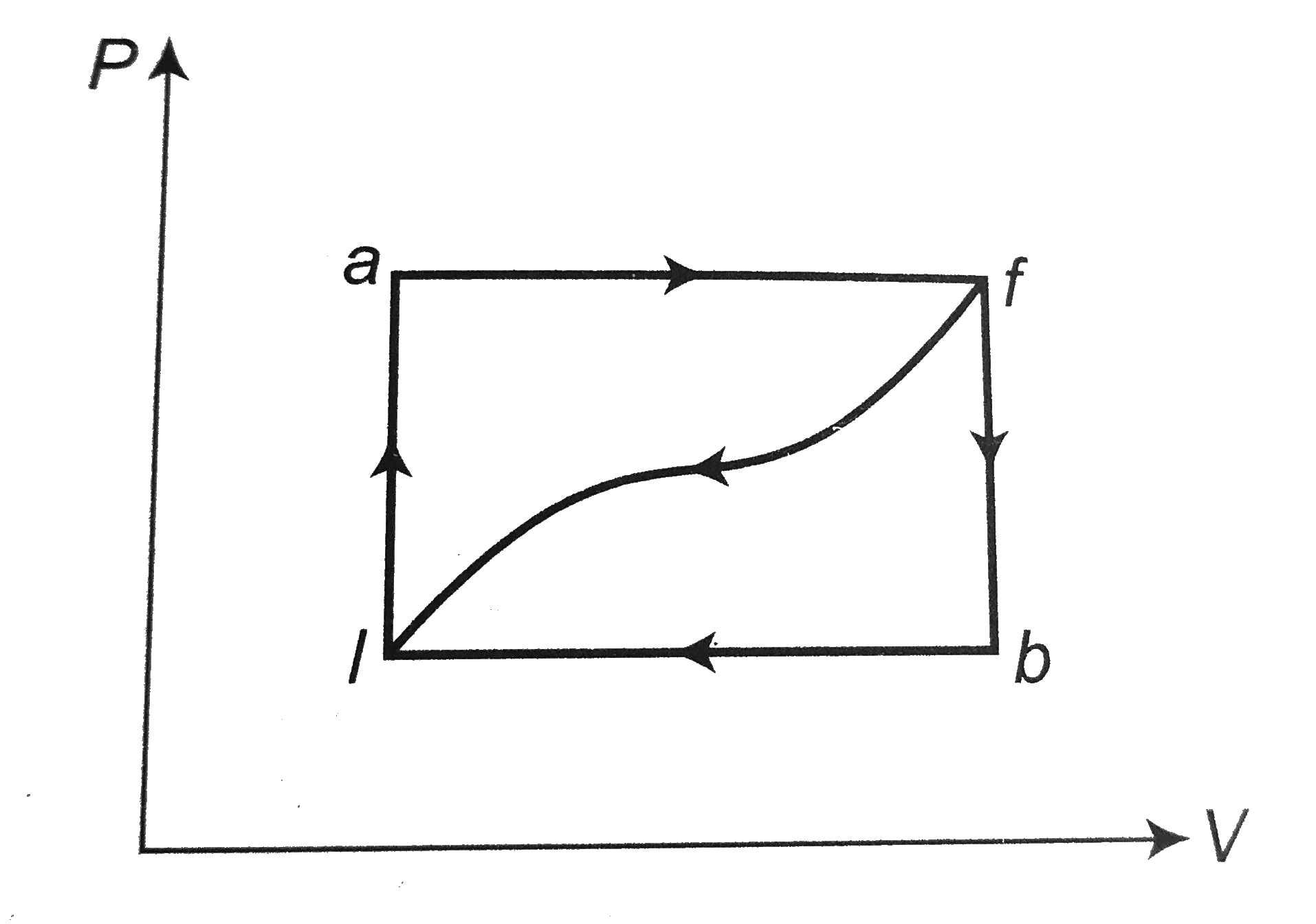 02:07View Solution
02:07View SolutionA thermodynamic system undergoes cyclic process `ABCDA` as shown in figure. The work done by the system is
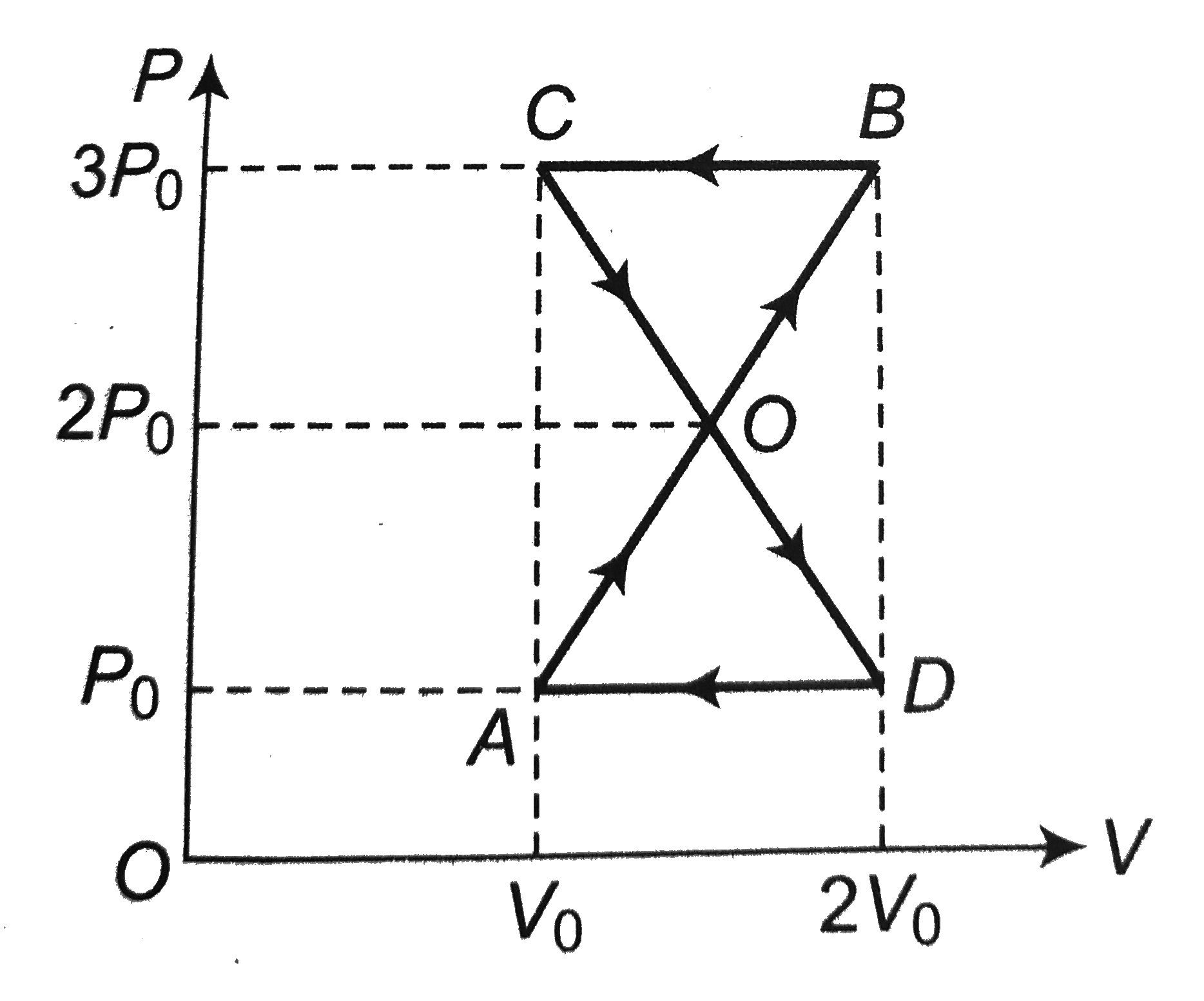 02:18View Solution
02:18View SolutionAn ideal gas is taken through the cycle `AtoBtoCtoA,` as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
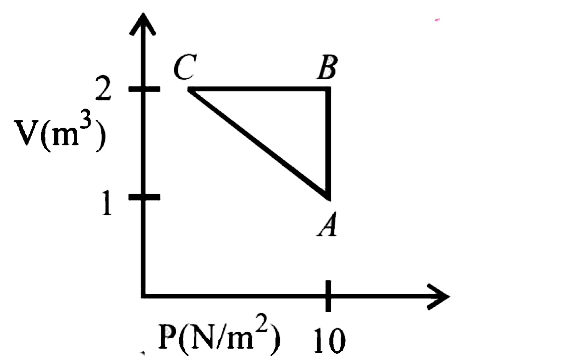 02:28View Solution
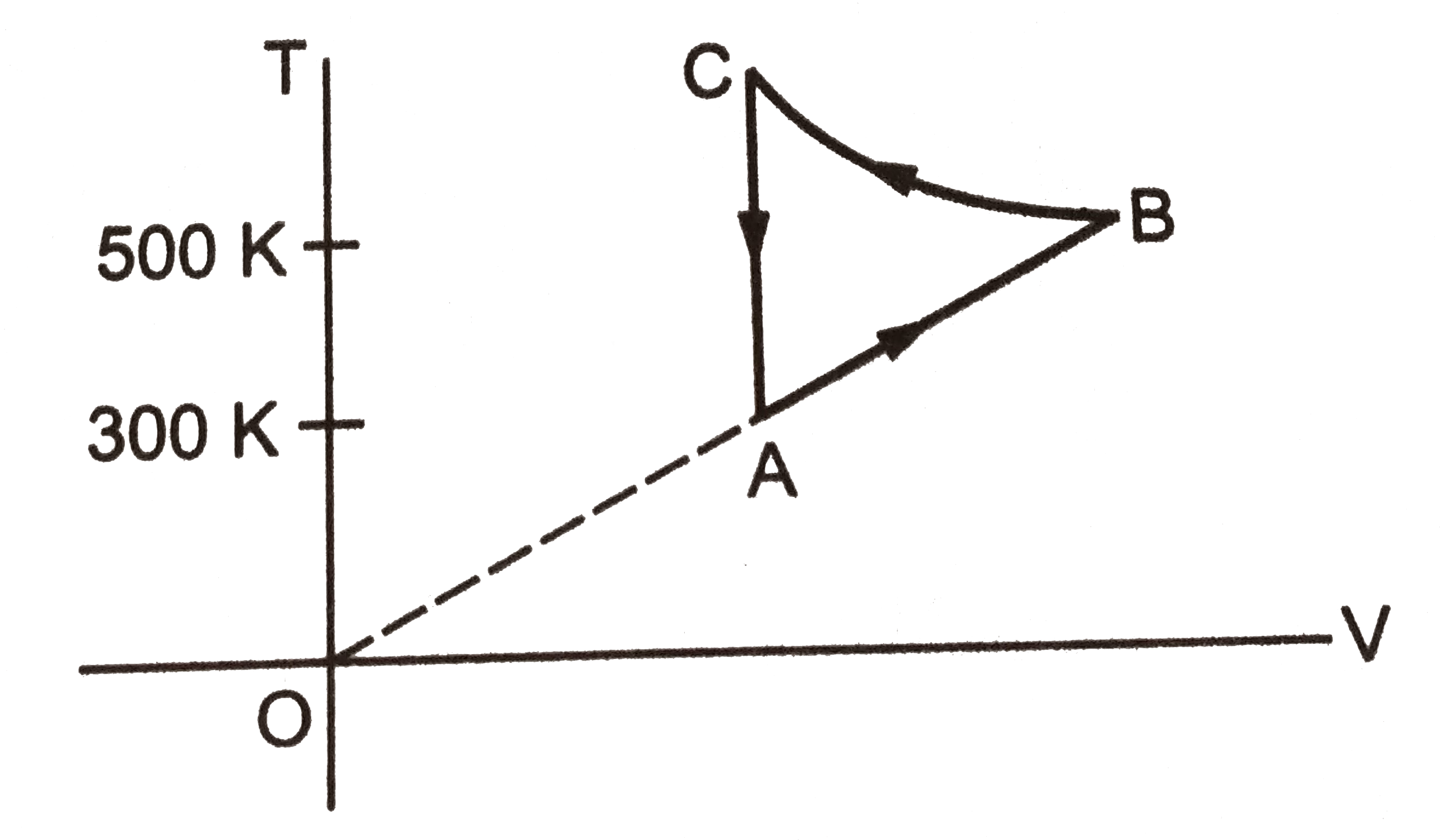
02:28View SolutionConsider the cyclic process ABCA, shown in figure, performed on a sample of `2.0 mol` of an ideal gas. A total of `1200 J` of heat is withdrawn from the sample in the process. Find the work done by the gas during the part BC.
 05:00View Solution
05:00View Solution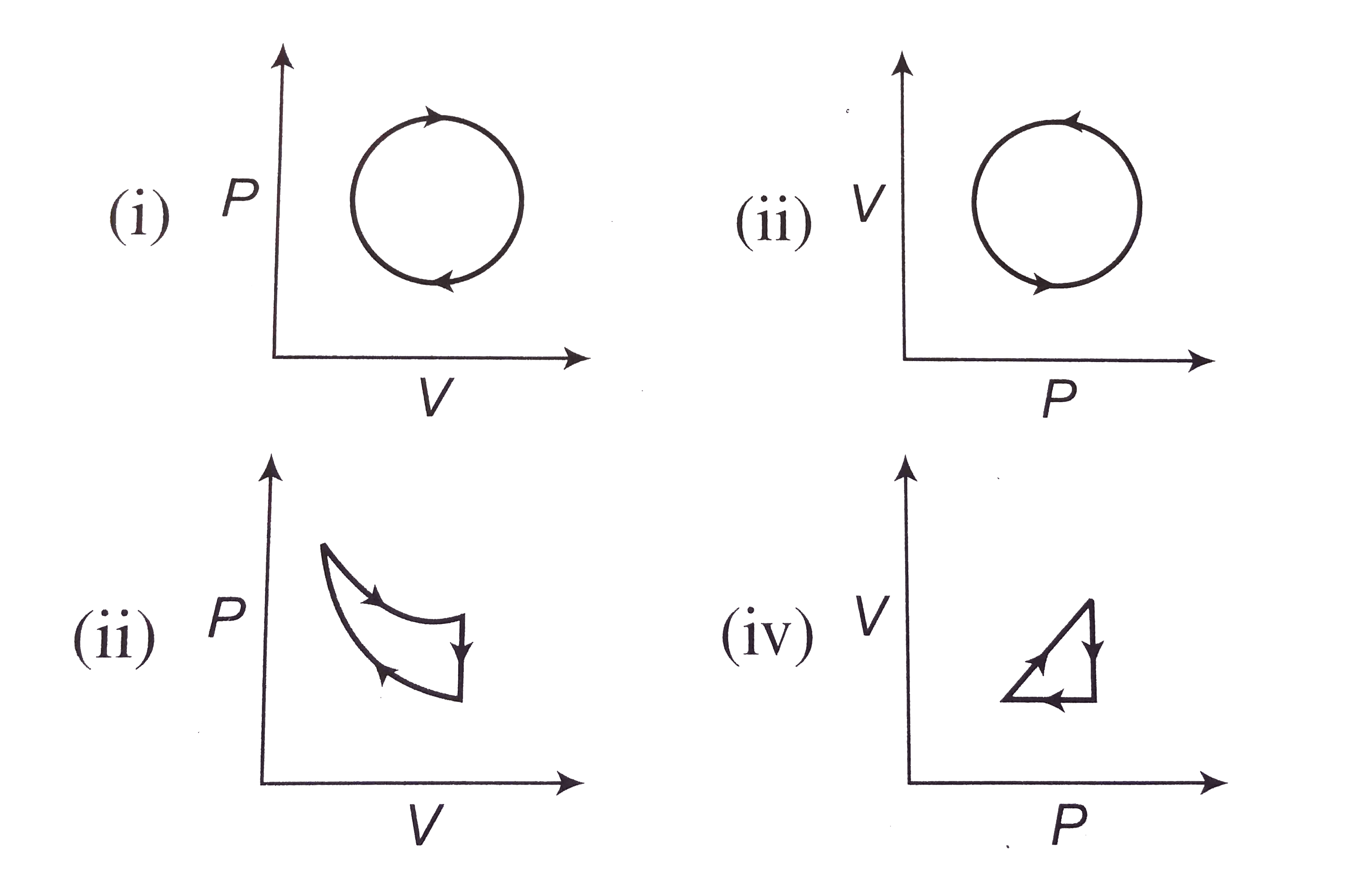
The following are the `P-V` diagrams for cyclic processes for a gas. In which of these processes is heat absorbed by the gas?06:39View Solution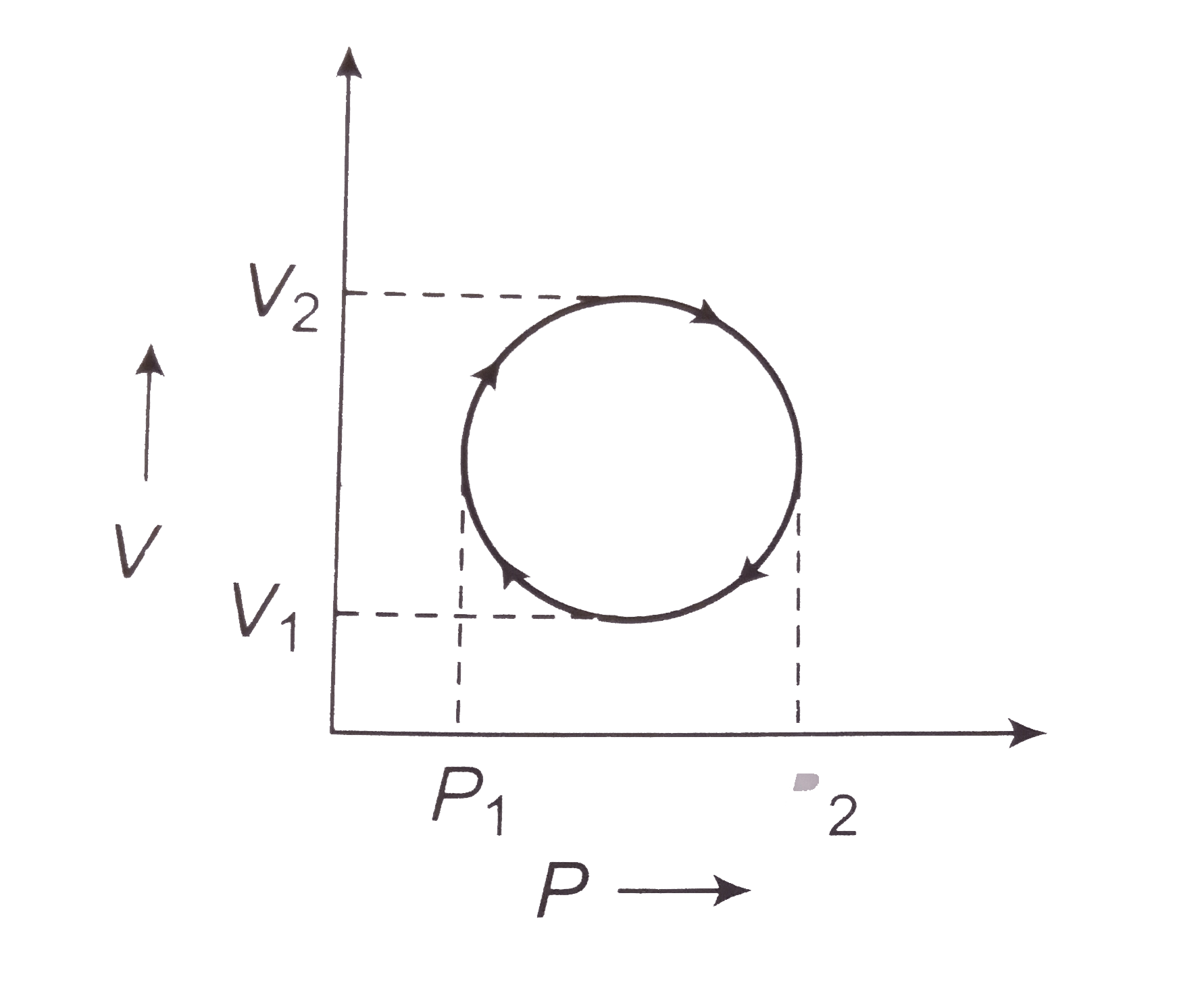
In the cyclic process shown in the `V-P` diagram the magnitude of the work is done is04:33View SolutionIn the previous question
(i) work is done by the gas
(ii) work is done on the gas
(iii) heat is absorbed by the gas
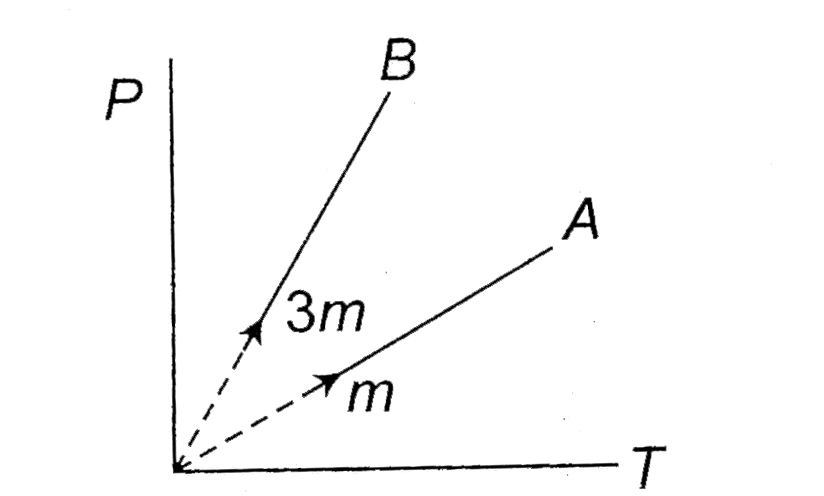
(iv) heat is given out by the gasView SolutionTwo different masses `m` and `3 m` of an ideal gas are heated separately in a vessel of constant volume, the pressure `P` and absolute temperature `T`, graphs for these two cases are shown in the figure as `A` and `B`. The ratio of slopes of curves `B` to `A` is
 03:02View Solution
03:02View Solution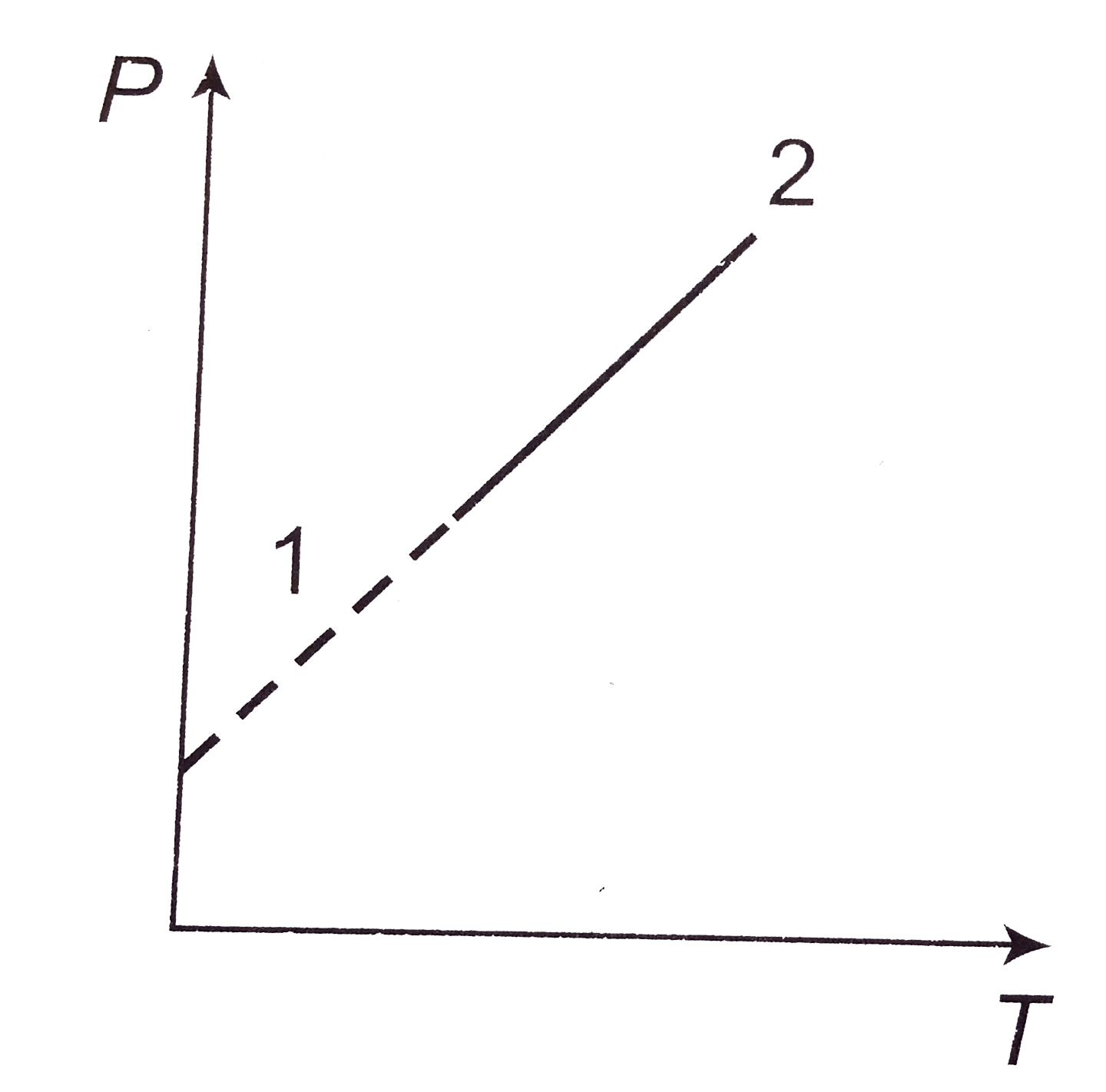
A pressure P, absolute temperature T, graph was obtained whe a given mass of a gas heated. During the heating process from the state 1 to the state 2, the volume03:16View SolutionA volume `V` absolute temperature `T` diagram was obtained when a given mass of gas was heated. During the heating process from state `1` to `2`, the pressure
_E01_062_Q01.png) 02:36View Solution
02:36View Solution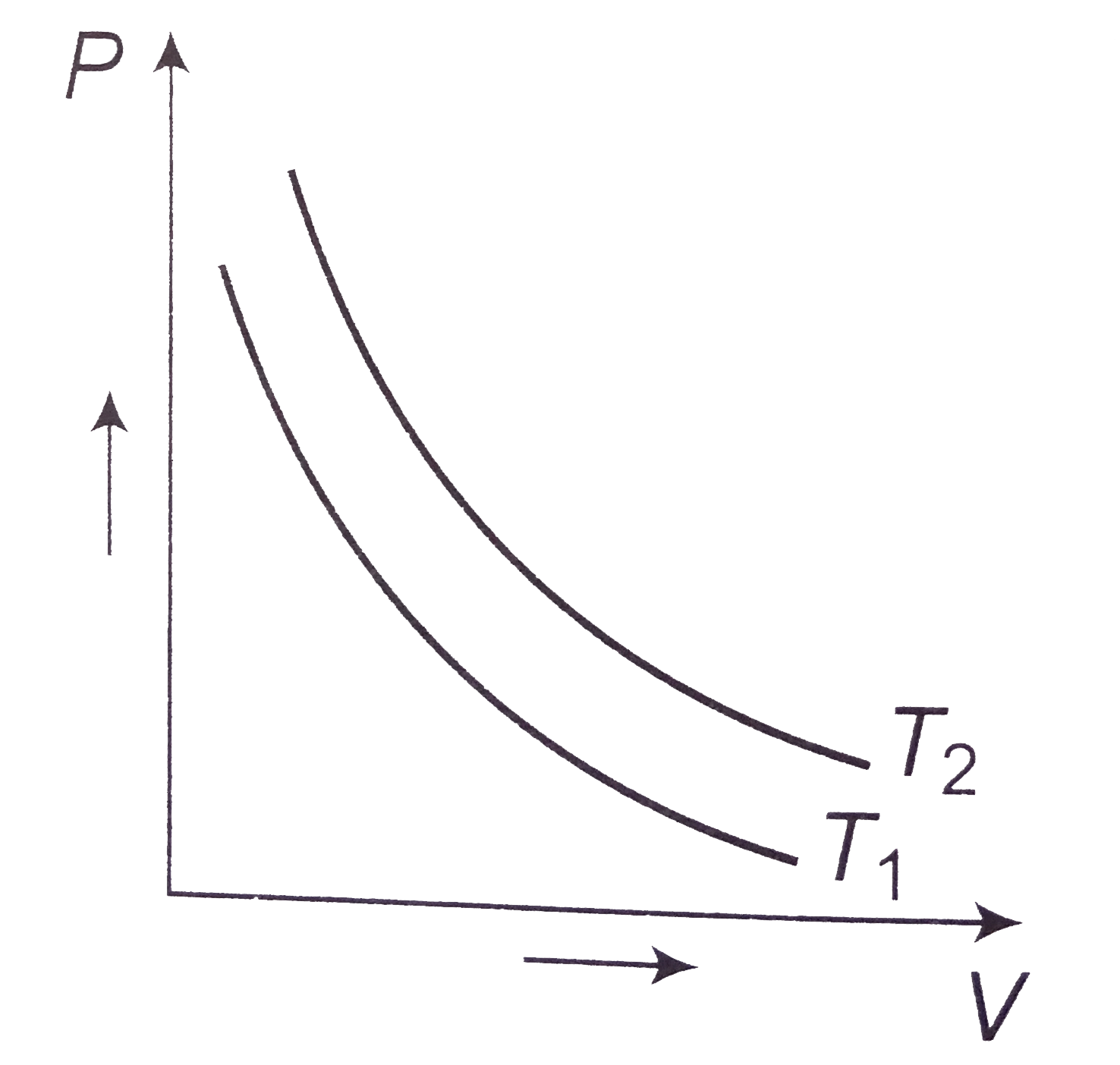
The adjoining figure shows graphs of pressure and volume of a gas at two temperature `T_1` and `T_2` Which of the following inferences is correct?02:09View Solution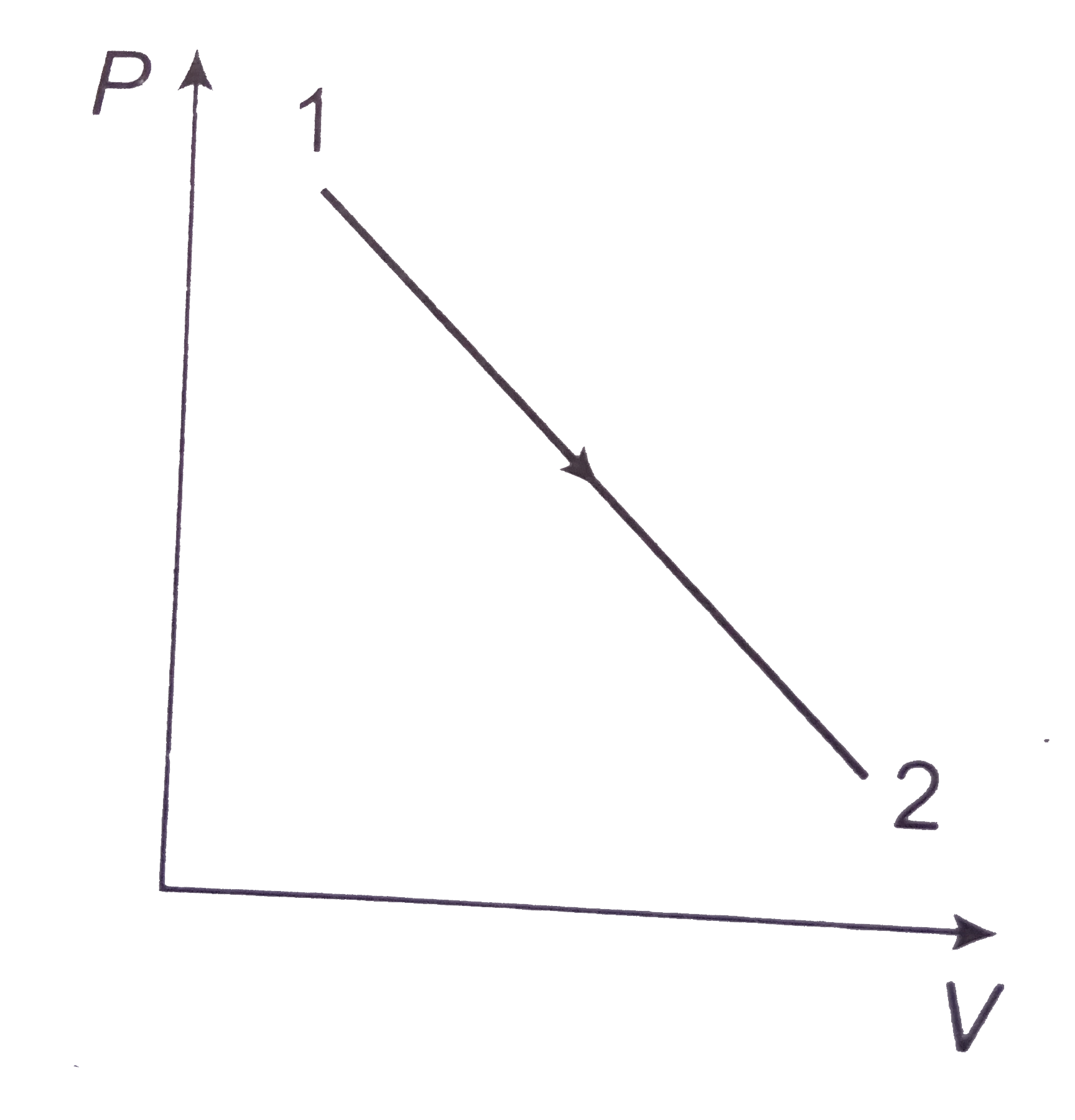
`P-V` graph was obtained from state 1 to state 2 when a given mass of a gas is subjected to temperature changes during the process the gas is03:15View SolutionA gas expands such that its initial and final temperature are equal . Also, the process followed by the gas traces a straight line on the `P-V` diagram:-
03:19View SolutionAn ideal gas is taken form the state `A(P,V)` to the state `B((P)/(2),2V)` along a straight line path in the `P-V` diagram.
Select the correct options
(i) The work done by the gas in the process A to B exceeds the work that would be done by it if the system were taken from A to B along the isotherm
(ii) In the `T-V` diagram, the path AB becomes part of a hyperbola
(iii) In the `P-T` diagram, the path AB becomes part of a hyperbola
(iv) In going from A to B, the temperature T of the first increases to maximum value and then decreases05:24View SolutionOne mole of an ideal gas goes from an initial state A to final state B via two processs : It first undergoes isothermal expansion from volume `V` to `3 V` and then its volume is reduced from `3 V` to `V` at constant pressure. The correct `P-V` diagram representing the two process in (figure)
01:54View SolutionOne mole of an ideal gas in initial state A undergoes a cyclic process ABCA, as shown in the figure. Its pressure at A is `P_0`. Choose the correct option (s) from the following
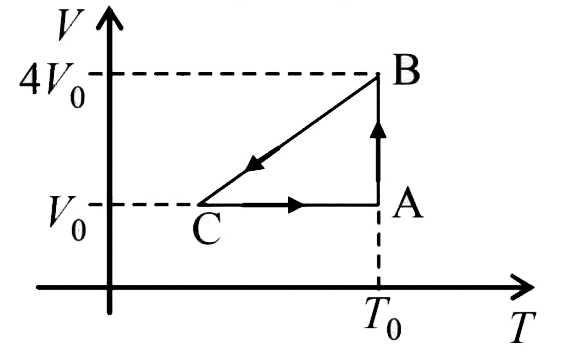 08:38View Solution
08:38View SolutionWhich of the following graphs correctly represents the variation of `beta=-(dV//dP)/V`
with P for an ideal gas at constant temperature?02:14View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by `DeltaV` due to an increase in temperature `DeltaT,` pressure remaining constant. The quantity `delta=(DeltaV)/(VDeltaT)` varies with temperature as
01:46View Solution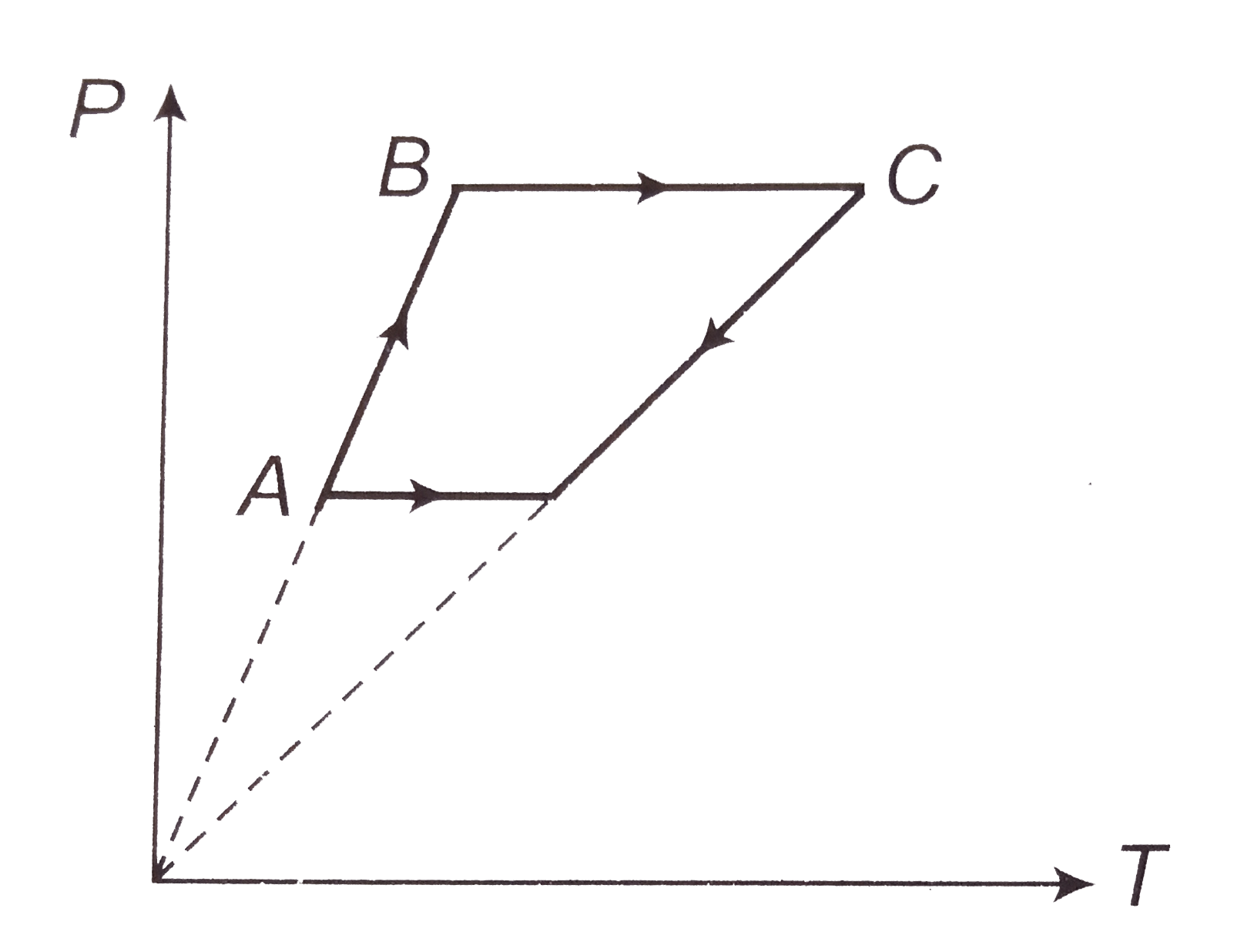
Six moles of an ideal gas performs a cycle shown in figure, the temperature are `T_A=600K,T_B=800K`,`T_C=2200K` and `T_D=1200K`, the work done per cycle is04:26View SolutionAssertion: The internal energy of an ideal gas does not change during an isothermal process.
Reason: The decrease in volume of a gas is compensated by a corresponding increase in perssure, when its temp. is held constant.01:45View SolutionFor an isothermal expansion of a perfect gas, the value of `(DeltaP)/(P)` is
01:26View SolutionIf heat is supplied to an ideal gas in an isothermal process.
01:40View SolutionIn an isothermal process on an ideal gas, the pressure increases by 0.5% . The volume decreases by about.
02:06View SolutionThe internal energy of a system remains constant when it undergoes
(i) a cyclic process
(ii) an isothermal process
(iii) an adiabatic process
(iv) any process in which the heat given out by the system equal to the work done on the system03:20View SolutionWhen an ideal gas in a cylinder was compreswsed isothermally by a piston, the work done on the gas found to be `1.5xx10^(4)` cal. During this process about
05:51View SolutionDuring an isothermal expansion, a confined ideal gas does `-150 J` of work aginst its surroundings. This implies that
02:07View SolutionA cyclic process is shown in the `P-T` siagram. Whech of the curves show the same process on a `P-V` diagram ?
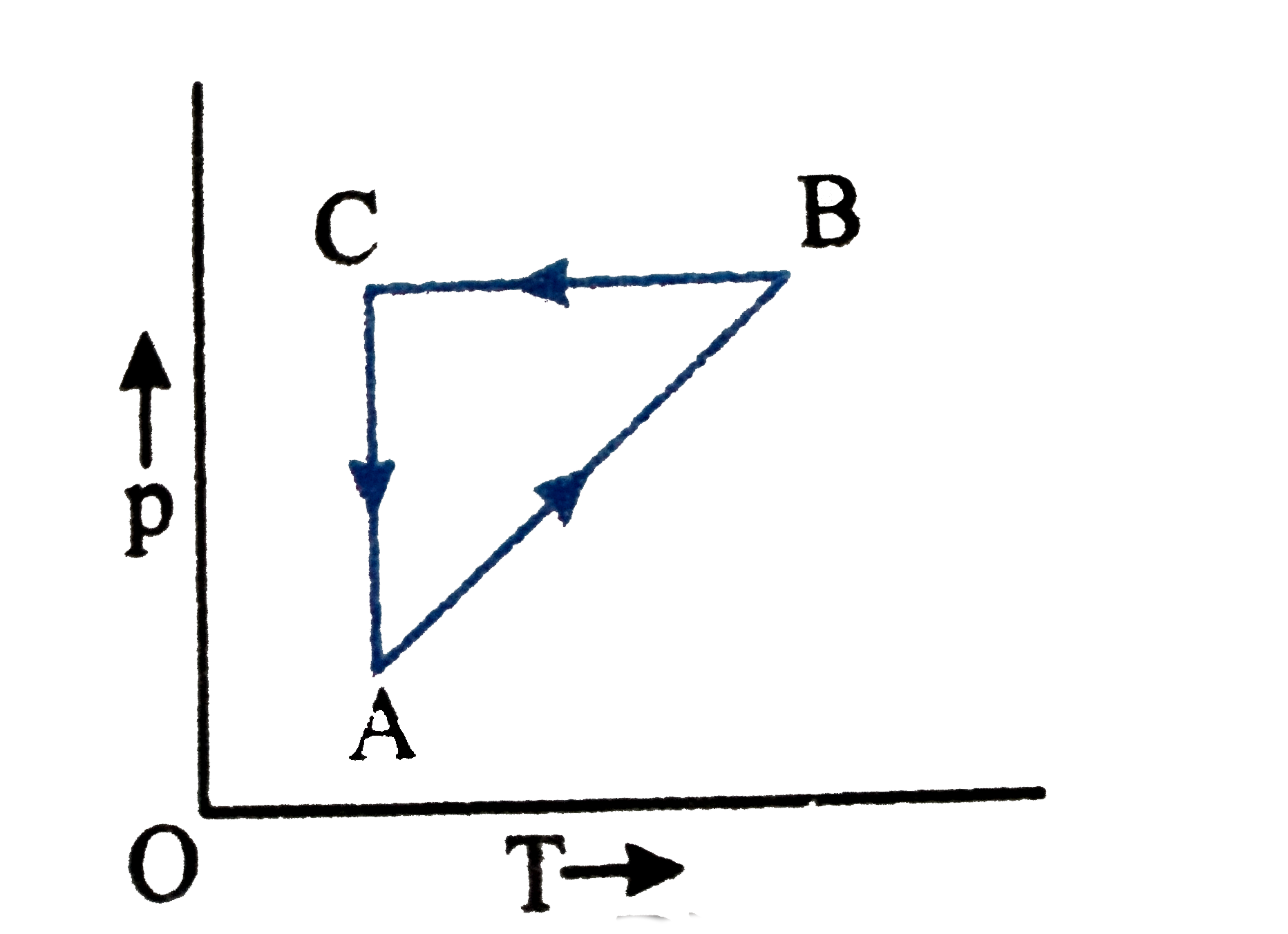 03:09View Solution
03:09View SolutionA cyclic process `ABCD` is shown is shown in the following `P-V` diagram. Which of the following curves represent the same process ?
 02:01View Solution
02:01View SolutionA cyclic process is shown on the P-T diagram. Which of the curve shown the same process on a V-T diagram?
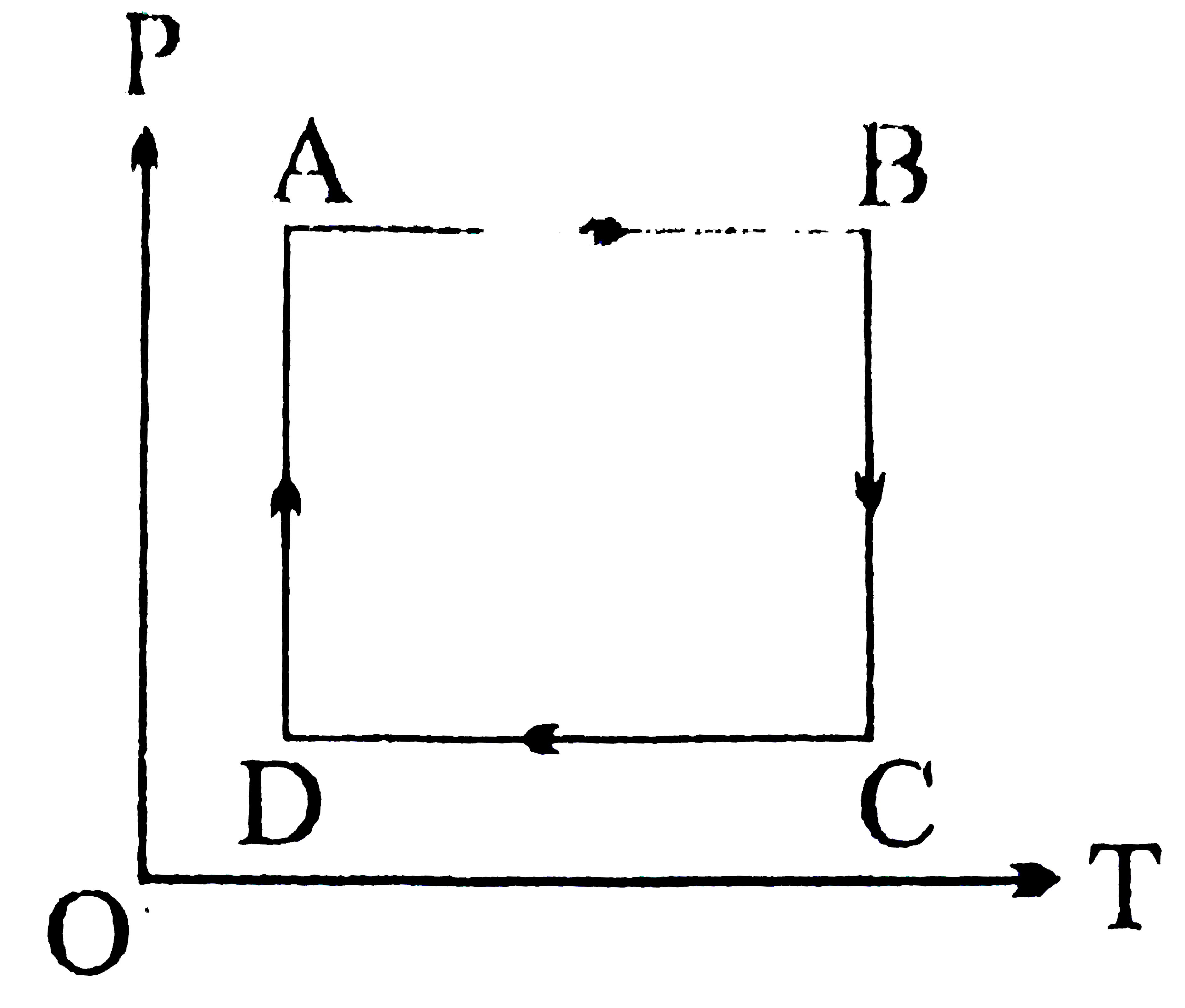 03:11View Solution
03:11View SolutionA gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
02:29View Solution
A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is `P_0` and temperature is `T_0`, atmospheric pressure is also `P_0`. Now the temperature of the gas is increased to `2T_0`, the tension in the wire will be03:20View SolutionThe latent heat of vaporisation of water is 2240 J/gm. If the work done in the process of expansion of 1 g of water is 168 J, then increase in internal energy is
01:31View SolutionWhen 1g of water at `0^@C` and `1xx10^5(N)/(m^2)` pressure is converted into ice of volume `1.091cm^3`. The external work done will e
01:18View SolutionA vessel containing 5 litres of a gas at 0.8 m pressure is connected to an evacuated vessel of volume 3 litres. The resultant pressure inside with be (assuming whole system to be isolated)
01:19View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are `P` and `T` for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
01:18View SolutionEach molecule of a gas has `f` degrees of freedom. The ratio `gamma` for the gas is
01:31View SolutionThe molar heat capacity of a gas at constant volumes is `C_V`. If `n` moles of the gas under `DeltaT` change in temperature it's internal energy will change by `nC_VDeltaT`
02:37View SolutionLet `(C_v) and (C_p)` denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively . Which of the following is a universal constant?
01:25View SolutionThe molar heat capacity for an ideal gas cannot
01:10View SolutionIf for a gas, `(R)/(C_V)=0.67`, the gas is
01:26View SolutionFor hydrogen gas `C_p-C_v=a` and for oxygen gas `C_p-C_v=b`,`C_p` and `C_v` being molar specific heats. The relation between a and b is
01:59View SolutionIf for hydrogen `s_p-s_v=a` and oxygen `s_p-s_v=b`, where `s_p` and `s_v` refer to specific heats at constant pressure and at constant volume then
02:44View SolutionThe ratio `(C_p)/(C_v)=gamma` for a gas. Its molecular weight is M. Its specific heat capacity at constant pressure is
02:12View Solution`C_p` is always greater than `C_v` for a gas, which of the following statements provide, partly or wholly, the reason for this?
(i) No work is done by a gas at constant volume
(ii) When a gas absorbs heat at constant pressure, its volume must change
(iii) For the same change in temperature, the internal energy of a gas changes by a smaller amount at constant volume that at constant pressure
(iv) The internal energy of an ideal gas is a function only of its temperature03:15View SolutionIf one mole of a monatomic gas `(gamma=5/3)` is mixed with one mole of a diatomic gas `(gamma=7/5),` the value of gamma for mixture is
03:02View SolutionA mixture of `n_1` moles of monoatomic gas and `n_2` moles of diatomic gas has `gamma=1.5`
04:31View SolutionWhen an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied, which increases the internal energy of the gas, is
02:20View SolutionA gas, for which `gamma` is `(4)/(3)` is heated at constant pressure. The percentage of heat supplied used for external work is
02:59View SolutionA monatomic gas expands at constant pressure on heating. The percentage of heat supplied that increases the internal energy of the gas and that is involed in the expansion is
02:13View Solution70 calories of heat required to raise the temperature of 2 moles of an ideal gas at constant pressure from `30^@Cto 35^@C.` The amount of heat required (in calories) to raise the temperature of the same gas through the same range `(30^@C to 35^@C)` at constant volume is:
03:29View SolutionThe average degrees of freedom per molecule for a gas are 6. The gas performs `25 J` of work when it expands at constant pressure. The heat absorbed by gas is
01:46View SolutionA rigid container of negligible heat capacity contains one mole of an ideal gas. The temperatures of the gas increases by `1^@C` if `3.0` cal of heat is added to it. The gas may be
02:41View SolutionWork done by a sample of an ideal gas in a process A is double the work done in another process B. The temperature rises through the same amount in the two processes. If `(C_A and C_B) be the molar heat capacities for the two processes,
03:14View SolutionIn case of water from `0` to `4^@C`
(i) Volume decreases and density of water is maximum at `4^@C`
(ii) `DeltaW` will be negative, since volume decreases
(iii) `C_p gt C_V`
(iv) `C_P lt C_V`04:28View SolutionA monoatomic gas of n-moles is heated temperature `T_1` to `T_2` under two different conditions
(i) at constant volume and
(ii) At constant pressure The change in internal energy of the gas is02:17View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
02:08View SolutionA monoatomic gas is supplied heat Q very slowly keeping the pressure constant. The work done by the gas is
05:39View SolutionWhich of the following is correct regarding adiabatic process
(i) In adiabatic process, all the three variables, P, V and T changes
(ii) In adiabatic process, the heat exchanged between system and surrounding is zero i.e., `DeltaQ=0`
(iii) Since `DeltaQ=nCDeltaT`, therefore for adiabatic process molar specific heat `C=0`
(iv) If a gas is suddenly expanded adiabatically temperature falls and if gas is adiabatically compressed, temperature rises03:07View SolutionWhich of the following is correct regarding adiabatic process
05:03View SolutionThe molar heat capacity for an ideal gas (i) Is zero for an adiabatic process
(ii) Is infinite for an isothermal process
(iii) depends only on the nature of the gas for a process in which either volume or pressure is constant
(iv) Is equal to the product of the molecular weight and specific heat capacity for any process03:55View SolutionFor an adiabatic expansion of a perfect gas, the value of `(DeltaP)/(P)` is equal to
03:11View SolutionIn an adiabatic process on a gas with `(gamma = 1.4)` the pressure is increased by `0.5%` . The volume decreases by about
03:28View SolutionDiatomic gas at pressure 'P' and volume 'V' is compressed adiabatically to 1/32 times the original volume. Then the final pressure is
02:01View SolutionAn ideal gas at `27^(@)C` is compressed adiabatically to `8//27` of its original volume. If `gamma = 5//3`, then the rise in temperature is
02:02View SolutionAn ideal gas at pressure of 1 atmosphere and temperature of `27^(@)C` is compressed adiabatically until its pressure becomes 8 times the initial pressure, then the final temperature is `(gamma=3//2)`
03:19View SolutionThe pressure and density of a diatomic gas `(gamma=7//5)` change adiabatically from (p,d) to `(p^('),d^('))`. If `(d^('))/(d)=32`, then `(P^('))/(P)` should be
02:38View SolutionA monoatomic ideal gas, initially at temperature `T_1,` is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature `T_2` by releasing the piston suddenly. If `L_1 and L_2` are the length of the gas column before expansion respectively, then `(T_1)/(T_2)` is given by
02:47View SolutionIn an adiabatic change, the pressure p and temperature T of a diatomic gas are related by the relation `ppropT^alpha`, where `alpha` equals
03:19View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
01:22View SolutionThe work of 146 kJ is performed in order to compress one kilo mole of a gas adiabatically and in this process the temperature of the gas increases by `7^@C`. The gas is `(R=8.3ml^-1Jmol^-1K^-1)`
02:39View SolutionThe adiabatic elasticity of hydrogen gas `(gamma=1.4)` at `NTP`
03:46View Solution`1mm^3` of a gas is compressed at 1 atmospheric pressure and temperature `27^@C` to `627^@C`. What is the final pressure under adiabatic condition `(gamma` for the gas `=1.5`)
04:35View SolutionFor which of the following processes is the entropy change zero,
01:26View SolutionIf a cylinder containing a gas at high pressure explodes, the gas undergoes
02:10View Solution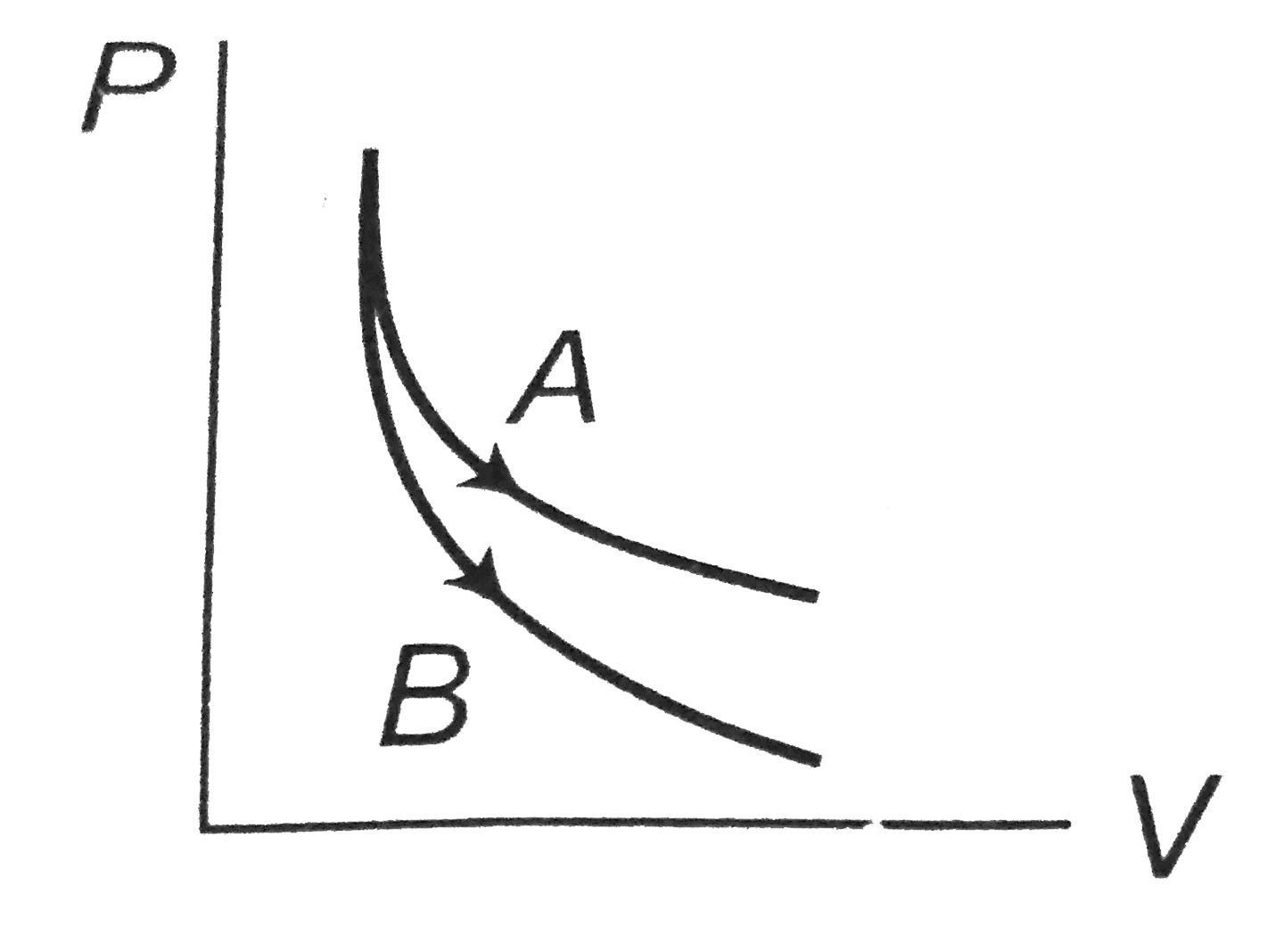
Consider the process A and B shown in the figure. It is possible that03:16View SolutionTwo gases have the same initial pressure, volume and temperature. They expand to the same final volume, one adiabatically and the other isothermally
08:32View Solution
EXERCISE questions and complete solutions for chapter LAWS OF THERMODYNAMICS of CP SINGH PHYSICS (HINGLISH) of Class 11
