Complete Solutions to बहुविकल्पीय प्रश्न of chapter बोध - संबद्ध प्रकार के प्रश्न of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | बोध - संबद्ध प्रकार के प्रश्न |
| BHARTI_BHAWAN | बहुविकल्पीय प्रश्न |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
विमीय समघातता के सिद्धांत के अनुसार किसी भी भौतिक सूत्र या समीकरण के बाएँ और दाएँ पक्षों के सभी पदों की विमाएँ समान होती है। उदाहरण के लिए `s=ut+1/2at^(2)` में पदों की संख्या 3 है तथा सभी के मात्रक और विमाएँ क्रमशः मीटर (m) तथा `"M"^(0)"L T"^(0)` है। इसी संदर्भ में न्यूटन के अनुसार तरल प्रवाह में स्पर्शीय प्रतिबल S की निर्भरता श्यानता गुणांक `(eta)` एवं वेग-प्रवणता `(dv)/(dr)` सूत्र `S=eta^(x)((dv)/(dr))^(y)` से व्यक्त की जाती है जहाँ `eta` की विमाएँ `"M L"^(-1)"T"^(-1)` है।
स्पर्शीय प्रतिबल की विमाएँ है।02:03View Solutionविमीय समघातता के सिद्धांत के अनुसार किसी भी भौतिक सूत्र या समीकरण के बाएँ और दाएँ पक्षों के सभी पदों की विमाएँ समान होती है। उदाहरण के लिए `s=ut+1/2at^(2)` में पदों की संख्या 3 है तथा सभी के मात्रक और विमाएँ क्रमशः मीटर (m) तथा `"M"^(0)"L T"^(0)` है। इसी संदर्भ में न्यूटन के अनुसार तरल प्रवाह में स्पर्शीय प्रतिबल S की निर्भरता श्यानता गुणांक `(eta)` एवं वेग-प्रवणता `(dv)/(dr)` सूत्र `S=eta^(x)((dv)/(dr))^(y)` से व्यक्त की जाती है जहाँ `eta` की विमाएँ `"M L"^(-1)"T"^(-1)` है।
x तथा y के मान है क्रमशः03:38View Solutionविमीय समघातता के सिद्धांत के अनुसार किसी भी भौतिक सूत्र या समीकरण के बाएँ और दाएँ पक्षों के सभी पदों की विमाएँ समान होती है। उदाहरण के लिए `s=ut+1/2at^(2)` में पदों की संख्या 3 है तथा सभी के मात्रक और विमाएँ क्रमशः मीटर (m) तथा `"M"^(0)"L T"^(0)` है। इसी संदर्भ में न्यूटन के अनुसार तरल प्रवाह में स्पर्शीय प्रतिबल S की निर्भरता श्यानता गुणांक `(eta)` एवं वेग-प्रवणता `(dv)/(dr)` सूत्र `S=eta^(x)((dv)/(dr))^(y)` से व्यक्त की जाती है जहाँ `eta` की विमाएँ `"M L"^(-1)"T"^(-1)` है।
श्यानता गुणांक का मात्रक है02:34View Solutionमुक्त आकाश में दो स्थिर आवेशों `q_(1)` तथा `q_(2)` के बीच की दूरी r हो, तो उनके बीच कार्यकारी बल
`F=(1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))`
तथा अनंत लंबाई के दो समांतर धारावाही चालकों के बीच एकांक लंबाई पर बल
`F=(mu_(0)I_(1)I_(2))/(2pi" "r)`
आधारी भौतिक राशियाँ द्रव्यमान (M), लंबाई (L), समय (T) तथा विधुत - धारा (A) मानते हुए नियतांक `in_(0)` तथा `mu_(0)` के SI मात्रक है04:06View Solutionमुक्त आकाश में दो स्थिर आवेशों `q_(1)` तथा `q_(2)` के बीच की दूरी r हो, तो उनके बीच कार्यकारी बल
`F=(1)/(4piepsilon_(0))(q_(1)q_(2))/(r^(2))`
तथा अनंत लंबाई के दो समांतर धारावाही चालकों के बीच एकांक लंबाई पर बल
`F=(mu_(0)I_(1)I_(2))/(2pi" "r)`
`in_(0)` तथा `mu_(0)` के किस संयोग से चाल की विमा प्राप्त होती है ?04:05View Solutionकिसी क्षैतिज नली से प्रति सेकंड प्रवाहित द्रव का आयतन V निम्नलिखित कारकों पर निर्भर करता है
(i) दाब - प्रवणता `(p)/(l)`,
जहाँ p = नली के सिरों पर दाबांतर, l = नली की लंबाई
(ii) नली के वृत्तीय काट का त्रिज्या r
(iii) द्रव का श्यानता गुणांक `eta`
अतः, V के लिए समीकरण है
`V=k(P/l)^(x)*r^(y)*eta^(z)`,
जहाँ k एक विमाहीन नियतांक है।
श्यानता गुणांक `eta` की विमाएँ वही है जो05:10View Solutionकिसी क्षैतिज नली से प्रति सेकंड प्रवाहित द्रव का आयतन V निम्नलिखित कारकों पर निर्भर करता है
(i) दाब - प्रवणता `(p)/(l)`,
जहाँ p = नली के सिरों पर दाबांतर, l = नली की लंबाई
(ii) नली के वृत्तीय काट का त्रिज्या r
(iii) द्रव का श्यानता गुणांक `eta`
अतः, V के लिए समीकरण है
`V=k(P/l)^(x)*r^(y)*eta^(z)`,
जहाँ k एक विमाहीन नियतांक है।
x,y,z के मान क्रमशः है07:14View Solutionकिसी क्षैतिज नली से प्रति सेकंड प्रवाहित द्रव का आयतन V निम्नलिखित कारकों पर निर्भर करता है
(i) दाब - प्रवणता `(p)/(l)`,
जहाँ p = नली के सिरों पर दाबांतर, l = नली की लंबाई
(ii) नली के वृत्तीय काट का त्रिज्या r
(iii) द्रव का श्यानता गुणांक `eta`
अतः, V के लिए समीकरण है
`V=k(P/l)^(x)*r^(y)*eta^(z)`,
जहाँ k एक विमाहीन नियतांक है।
इस प्रश्न के विवरण से प्राप्त समीकरण को कहा जाता है02:00View Solutionप्रक्षेप्य की गति में प्रक्षेप - पथ का स्वरूप परवलीय होता है तथा प्रक्षेप - कोण `theta=45^(@)` के लिए क्षैतिज परास महत्तम होता है। किसी बिंदु से दो कण A एवं B समान चाल u से क्षैतिज तल के सापेक्ष `alpha` और `beta` कोण `(alpha!=beta!=45^(@))` बनाते हुए फेंके गए है जिनके लिए क्षैतिज परास R समान है।
प्रक्षेप - कोण `alpha` तथा `beta` के लिए आवश्यक शर्त है04:41View Solutionप्रक्षेप्य की गति में प्रक्षेप - पथ का स्वरूप परवलीय होता है तथा प्रक्षेप - कोण `theta=45^(@)` के लिए क्षैतिज परास महत्तम होता है। किसी बिंदु से दो कण A एवं B समान चाल u से क्षैतिज तल के सापेक्ष `alpha` और `beta` कोण `(alpha!=beta!=45^(@))` बनाते हुए फेंके गए है जिनके लिए क्षैतिज परास R समान है।
यदि समान क्षैतिज R के लिए A एवं B द्वारा प्राप्त महत्तम ऊँचाई क्रमशः `h_(1)` तथा `h_(2)` हो तब03:35View Solutionप्रक्षेप्य की गति में प्रक्षेप - पथ का स्वरूप परवलीय होता है तथा प्रक्षेप - कोण `theta=45^(@)` के लिए क्षैतिज परास महत्तम होता है। किसी बिंदु से दो कण A एवं B समान चाल u से क्षैतिज तल के सापेक्ष `alpha` और `beta` कोण `(alpha!=beta!=45^(@))` बनाते हुए फेंके गए है जिनके लिए क्षैतिज परास R समान है।
A एवं B के उड़ान - काल क्रमशः `h_(1)` तथा `h_(2)` हो, तब03:22View Solutionसरल रेखा क्षैतिज दिशा में गतिशील किसी ब्लॉक का त्वरण समय के फलन के रूप में
`a(t)=alphat-betat^(2)`
द्वारा व्यक्त किया जाता है समय `t=0` पर ब्लॉक विरामावस्था में है तथा सभी सतह घर्षणमुक्त है।
समय (t) के फलन के रूप में ब्लॉक का वेग व्यक्त होगा01:36View Solutionसरल रेखा क्षैतिज दिशा में गतिशील किसी ब्लॉक का त्वरण समय के फलन के रूप में
`a(t)=alphat-betat^(2)`
द्वारा व्यक्त किया जाता है समय `t=0` पर ब्लॉक विरामावस्था में है तथा सभी सतह घर्षणमुक्त है।
ब्लॉक के कहहतम वेग का मान है02:59View Solutionसरल रेखा क्षैतिज दिशा में गतिशील किसी ब्लॉक का त्वरण समय के फलन के रूप में
`a(t)=alphat-betat^(2)`
द्वारा व्यक्त किया जाता है समय `t=0` पर ब्लॉक विरामावस्था में है तथा सभी सतह घर्षणमुक्त है।
समय (t) के फलन के रूप में ब्लॉक की स्थिति x(t) व्यक्त होगी02:43View Solutionसरल रेखा क्षैतिज दिशा में गतिशील किसी ब्लॉक का त्वरण समय के फलन के रूप में
`a(t)=alphat-betat^(2)`
द्वारा व्यक्त किया जाता है समय `t=0` पर ब्लॉक विरामावस्था में है तथा सभी सतह घर्षणमुक्त है।
ब्लॉक के कहहतम वेग का मान है02:59View Solutionसरल रेखा में गतिशील किसी कण के तात्कालिक वेग v को स्थिति x के फलन के रूप में समीकरण `v=v_(0)+kx` से व्यक्त किया जाता है, जहाँ k एक नियतांक है तथा वेग का विचरण x के सापेक्ष रैखिकतः होता है
कण का तात्कालिक त्वरण a है, जहाँ01:56View Solutionसरल रेखा में गतिशील किसी कण के तात्कालिक वेग v को स्थिति x के फलन के रूप में समीकरण `v=v_(0)+kx` से व्यक्त किया जाता है, जहाँ k एक नियतांक है तथा वेग का विचरण x के सापेक्ष रैखिकतः होता है
कण के वेग को `v_(0)` से `2v_(0)` बढ़कर होने में लगा समय होगा02:53View Solutionसरल रेखा में गतिशील किसी कण के तात्कालिक वेग v को स्थिति x के फलन के रूप में समीकरण `v=v_(0)+kx` से व्यक्त किया जाता है, जहाँ k एक नियतांक है तथा वेग का विचरण x के सापेक्ष रैखिकतः होता है
कण के वेग v एवं स्थिति x के बीच खींचे गए ग्राफ की प्रकृति है।01:49View Solutionm तथा 2m द्रव्यमान के दो ब्लॉक एक आदर्श डोरी से बँधे है तथा एक घर्षणरहित क्षैतिज समतल पर स्थित है (चित्र 4.1) | किसी एक ब्लॉक (2m) पर क्षैतिज दिशा में बल F आरोपित कर निकाय को खींचा जा रहा है

निकाय का उभयनिष्ठ त्वरण है01:23View Solutionm तथा 2m द्रव्यमान के दो ब्लॉक एक आदर्श डोरी से बँधे है तथा एक घर्षणरहित क्षैतिज समतल पर स्थित है (चित्र 4.1) | किसी एक ब्लॉक (2m) पर क्षैतिज दिशा में बल F आरोपित कर निकाय को खींचा जा रहा है

दोनों ब्लॉकों को जोड़ने वाली दोसी में तनाव है03:31View Solutionm तथा 2m द्रव्यमान के दो ब्लॉक एक आदर्श डोरी से बँधे है तथा एक घर्षणरहित क्षैतिज समतल पर स्थित है (चित्र 4.1) | किसी एक ब्लॉक (2m) पर क्षैतिज दिशा में बल F आरोपित कर निकाय को खींचा जा रहा है

यदि बल F को 2m द्रव्यमान वाले ब्लॉक पर नहीं लगाया जाऐ, बल्कि m द्रव्यमान के ब्लॉक पर क्षैतिजतः बाईं ओर की दिशा में लगाया जाऐ, तब05:14View Solutionm तथा 2m द्रव्यमान के दो ब्लॉक एक आदर्श डोरी से बँधे है तथा एक घर्षणरहित क्षैतिज समतल पर स्थित है (चित्र 4.1) | किसी एक ब्लॉक (2m) पर क्षैतिज दिशा में बल F आरोपित कर निकाय को खींचा जा रहा है

यदि दोनों ब्लॉकों को जोड़नेवाली डोरी को निकाय की गति के क्रम में अचानक काट दिया जाऐ तब02:39View Solutionद्रव्यमान M तथा m के दो ब्लॉक `(M gt m)` किसी आदर्श डोरी के सिरों से बँधे है तथा डोरी एक चिकनी एवं हलकी घिरनी से गुजरती है (चित्र 4.2)
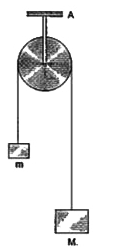 03:54View Solution
03:54View Solutionद्रव्यमान M तथा m के दो ब्लॉक `(M gt m)` किसी आदर्श डोरी के सिरों से बँधे है तथा डोरी एक चिकनी एवं हलकी घिरनी से गुजरती है (चित्र 4.2)
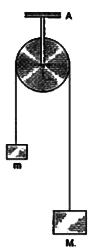 04:31View Solution
04:31View Solutionद्रव्यमान M तथा m के दो ब्लॉक `(M gt m)` किसी आदर्श डोरी के सिरों से बँधे है तथा डोरी एक चिकनी एवं हलकी घिरनी से गुजरती है (चित्र 4.2)
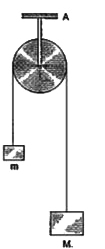 04:14View Solution
04:14View Solutionद्रव्यमान M तथा m के दो ब्लॉक `(M gt m)` किसी आदर्श डोरी के सिरों से बँधे है तथा डोरी एक चिकनी एवं हलकी घिरनी से गुजरती है (चित्र 4.2)
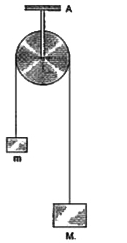 03:54View Solution
03:54View Solutionत्रिज्या R का एक दृढ अर्धगोला किसी क्षैतिज समतल से जुड़ा है तथा इसकी गोलीय सतह घर्षणरहित है (चित्र 4.3) गोले के उच्चतम बिंदु A से m द्रव्यमान का एक ब्लॉक फिसलना प्रारंभ करता है तथा P बिंदु पर इसका संपर्क गोले से छूट जाता है गोलीय तल की त्रिज्या R तथा `angleAOP=theta`.
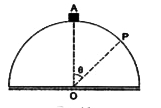
यदि बिंदु A पर ब्लॉक पर आरोपित अभिलंब प्रतिक्रिया `N_(A)` हो, तो02:14View Solutionत्रिज्या R का एक दृढ अर्धगोला किसी क्षैतिज समतल से जुड़ा है तथा इसकी गोलीय सतह घर्षणरहित है (चित्र 4.3) गोले के उच्चतम बिंदु A से m द्रव्यमान का एक ब्लॉक फिसलना प्रारंभ करता है तथा P बिंदु पर इसका संपर्क गोले से छूट जाता है गोलीय तल की त्रिज्या R तथा `angleAOP=theta`.
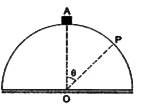
बिंदु A से P तक आने के क्रम में03:25View Solutionत्रिज्या R का एक दृढ अर्धगोला किसी क्षैतिज समतल से जुड़ा है तथा इसकी गोलीय सतह घर्षणरहित है (चित्र 4.3) गोले के उच्चतम बिंदु A से m द्रव्यमान का एक ब्लॉक फिसलना प्रारंभ करता है तथा P बिंदु पर इसका संपर्क गोले से छूट जाता है गोलीय तल की त्रिज्या R तथा `angleAOP=theta`.
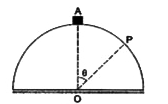
बिंदु P संपर्क छूटते समय यदि ब्लॉक की v चाल हो, तो03:12View Solutionत्रिज्या R का एक दृढ अर्धगोला किसी क्षैतिज समतल से जुड़ा है तथा इसकी गोलीय सतह घर्षणरहित है (चित्र 4.3) गोले के उच्चतम बिंदु A से m द्रव्यमान का एक ब्लॉक फिसलना प्रारंभ करता है तथा P बिंदु पर इसका संपर्क गोले से छूट जाता है गोलीय तल की त्रिज्या R तथा `angleAOP=theta`.
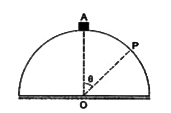
संपर्क छूटते समय कोण `theta` का मान होगा |02:42View Solutionत्रिज्या R का एक दृढ अर्धगोला किसी क्षैतिज समतल से जुड़ा है तथा इसकी गोलीय सतह घर्षणरहित है (चित्र 4.3) गोले के उच्चतम बिंदु A से m द्रव्यमान का एक ब्लॉक फिसलना प्रारंभ करता है तथा P बिंदु पर इसका संपर्क गोले से छूट जाता है गोलीय तल की त्रिज्या R तथा `angleAOP=theta`.

संपर्क छूटते समय यदि ब्लॉक की क्षैतिज समतल से ऊर्ध्वाधर ऊँचाई h हो, तो02:09View Solutionक्षैतिज से `alpha` कोण पर झुके किसी आनत तल (चित्र 4.4) पर सामान द्रव्यमान m के दो ब्लॉक स्थिर अवस्था में स्थिर है सभी सतहें घर्षणमुक्त है तथा दोनों डोरियाँ हलकी एवं अवितान्य है।
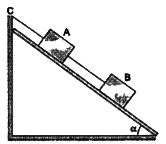
ब्लॉक A एवं B को जोड़नेवाली डोरी में तनाव है01:55View Solutionक्षैतिज से `alpha` कोण पर झुके किसी आनत तल (चित्र 4.4) पर सामान द्रव्यमान m के दो ब्लॉक स्थिर अवस्था में स्थिर है सभी सतहें घर्षणमुक्त है तथा दोनों डोरियाँ हलकी एवं अवितान्य है।
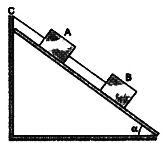
ब्लॉक A को ऊर्ध्वाधर दीवार से जोड़नेवाली डोरी में तनाव है02:11View Solutionक्षैतिज से `alpha` कोण पर झुके किसी आनत तल (चित्र 4.4) पर सामान द्रव्यमान m के दो ब्लॉक स्थिर अवस्था में स्थिर है सभी सतहें घर्षणमुक्त है तथा दोनों डोरियाँ हलकी एवं अवितान्य है।

यदि A एवं B को जोड़ने वाली डोरी को अचानक काट दिया जाए, तब04:00View Solutionएक चिकने क्षैतिज समतल पर रखे m तथा 2m द्रव्यमान के दो ब्लॉकों को एक आदर्श स्प्रिंग (बल नियतांक = k) से जोड़ा गया (चित्र 4.5) | 2m द्रवमानवाले ब्लॉक को तीव्र आवेग देने पर वह दाहिनी ओर `v_(0)` वेग प्राप्त करता है।
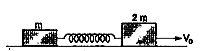
निकाय के द्रव्यमान केंद्र का वेग है01:36View Solutionएक चिकने क्षैतिज समतल पर रखे m तथा 2m द्रव्यमान के दो ब्लॉकों को एक आदर्श स्प्रिंग (बल नियतांक = k) से जोड़ा गया (चित्र 4.5) | 2m द्रवमानवाले ब्लॉक को तीव्र आवेग देने पर वह दाहिनी ओर `v_(0)` वेग प्राप्त करता है।
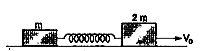
निकाय के द्रव्यमान केंद्र का वेग है01:36View Solutionएक चिकने क्षैतिज समतल पर रखे m तथा 2m द्रव्यमान के दो ब्लॉकों को एक आदर्श स्प्रिंग (बल नियतांक = k) से जोड़ा गया (चित्र 4.5) | 2m द्रवमानवाले ब्लॉक को तीव्र आवेग देने पर वह दाहिनी ओर `v_(0)` वेग प्राप्त करता है।

स्प्रिंग का महत्तम प्रसार होने पर02:21View Solutionएक चिकने क्षैतिज समतल पर रखे m तथा 2m द्रव्यमान के दो ब्लॉकों को एक आदर्श स्प्रिंग (बल नियतांक = k) से जोड़ा गया (चित्र 4.5) | 2m द्रवमानवाले ब्लॉक को तीव्र आवेग देने पर वह दाहिनी ओर `v_(0)` वेग प्राप्त करता है।

स्प्रिंग का महत्तम प्रसार होगा02:45View Solutionचित्र `4.6` में प्रदर्शित व्यवस्था संतुलन में स्थिर है जिसमें `m_(1)=2" kg",m_(2)=8" kg",k_(1)=50" N m"^(-1),k_(2)=70" N m"^(-1)` तथा स्प्रिंग 2 में 50 cm का संकुचन है दोनों स्प्रिंग की स्वाभाविक लंबाई समान है दोनों ब्लॉक से संबद्ध धागा हल्का ओर अवितान्य है।
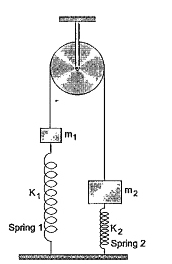
स्प्रिंग 1 में प्रसार है03:32View Solutionचित्र `4.6` में प्रदर्शित व्यवस्था संतुलन में स्थिर है जिसमें `m_(1)=2" kg",m_(2)=8" kg",k_(1)=50" N m"^(-1),k_(2)=70" N m"^(-1)` तथा स्प्रिंग 2 में 50 cm का संकुचन है दोनों स्प्रिंग की स्वाभाविक लंबाई समान है दोनों ब्लॉक से संबद्ध धागा हल्का ओर अवितान्य है।
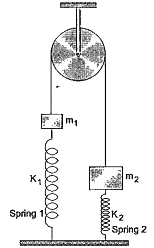
धागे में तनाव है02:13View Solutionचित्र `4.6` में प्रदर्शित व्यवस्था संतुलन में स्थिर है जिसमें `m_(1)=2" kg",m_(2)=8" kg",k_(1)=50" N m"^(-1),k_(2)=70" N m"^(-1)` तथा स्प्रिंग 2 में 50 cm का संकुचन है दोनों स्प्रिंग की स्वाभाविक लंबाई समान है दोनों ब्लॉक से संबद्ध धागा हल्का ओर अवितान्य है।

स्प्रिंग 1 को काट देने के तुरंत बाद ब्लॉक `m_(2)` का तात्क्षणिक त्वरण होगा04:12View Solutionएक चिकने क्षैतिज समतल पर किसी कण की तिरछी अप्रत्यास्थ टक्कर का प्रभाव वेग के परिमाण एवं दिशा में परिवर्तन लाता है जो टक्कर के प्रत्यावस्थान गुणांक e पर निर्भर करता है इस गुणांक e को निम्नलिखित संबंध से परिभाषित किया जाता है।
पृथक्करण का वेग `=e xx` उपगमन का वेग
चित्र `4.7` के अनुसार प्रत्यावस्थान गुणांक e का मान है
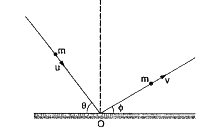 03:30View Solution
03:30View Solutionएक चिकने क्षैतिज समतल पर किसी कण की तिरछी अप्रत्यास्थ टक्कर का प्रभाव वेग के परिमाण एवं दिशा में परिवर्तन लाता है जो टक्कर के प्रत्यावस्थान गुणांक e पर निर्भर करता है इस गुणांक e को निम्नलिखित संबंध से परिभाषित किया जाता है।
पृथक्करण का वेग `=e xx` उपगमन का वेग
कण की अंतिम एवं प्रारंभिक गतिज ऊर्जा का अनुपात है07:54View Solutionएक चिकने क्षैतिज समतल पर किसी कण की तिरछी अप्रत्यास्थ टक्कर का प्रभाव वेग के परिमाण एवं दिशा में परिवर्तन लाता है जो टक्कर के प्रत्यावस्थान गुणांक e पर निर्भर करता है इस गुणांक e को निम्नलिखित संबंध से परिभाषित किया जाता है।
पृथक्करण का वेग `=e xx` उपगमन का वेग
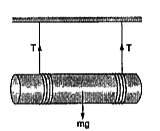
क्षैतिज समतल द्वारा कण को प्रदान किया गया आवेग है06:02View Solutionचित्र 4.8 में प्रदर्शित द्रव्यमान m तथा त्रिज्या R के एक ठोस बेलन पर दो अवितान्य धागो को लपेटकर दृढ आधार से लटकाया गया है धागो पर बेलन की गति गुरुत्व के अधीन पूर्णतः लोटनिक है।
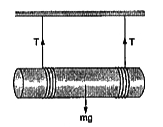
बेलन की गति में यदि रैखिक त्वरण a हो, तो `(a)/(g)` का मान है03:43View Solutionचित्र 4.8 में प्रदर्शित द्रव्यमान m तथा त्रिज्या R के एक ठोस बेलन पर दो अवितान्य धागो को लपेटकर दृढ आधार से लटकाया गया है धागो पर बेलन की गति गुरुत्व के अधीन पूर्णतः लोटनिक है।

प्रत्येक धागे में तनाव T हो, तो03:54View Solutionचित्र 4.8 में प्रदर्शित द्रव्यमान m तथा त्रिज्या R के एक ठोस बेलन पर दो अवितान्य धागो को लपेटकर दृढ आधार से लटकाया गया है धागो पर बेलन की गति गुरुत्व के अधीन पूर्णतः लोटनिक है।
यदि बेलन को विराम से चलकर ऊर्ध्वाधरतः h दूरी तय करने पर वेग v प्राप्त हो, तो02:59View Solutionचित्र 4.9 में प्रदर्शित व्यवस्था में अवितान्य डोरी से जुड़े दो ब्लॉक जिनके द्रव्यमान क्रमशः m तथा 4m है, एक भारतरहित घिरनी से होकर गुजरते है द्रव्यमान 4m के ब्लॉक को h ऊँचाई से विरामावस्था से मुक्त किया जाता है।
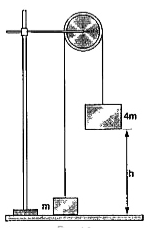
ब्लॉक की गति के क्रम में उनका उभयनिष्ठ त्वरण है02:04View Solutionचित्र 4.9 में प्रदर्शित व्यवस्था में अवितान्य डोरी से जुड़े दो ब्लॉक जिनके द्रव्यमान क्रमशः m तथा 4m है, एक भारतरहित घिरनी से होकर गुजरते है द्रव्यमान 4m के ब्लॉक को h ऊँचाई से विरामावस्था से मुक्त किया जाता है।
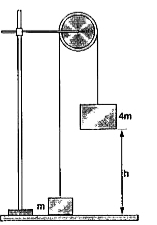
ब्लॉक की गति के क्रम में सम्बद्ध डोरी में तनाव है02:31View Solutionचित्र 4.9 में प्रदर्शित व्यवस्था में अवितान्य डोरी से जुड़े दो ब्लॉक जिनके द्रव्यमान क्रमशः m तथा 4m है, एक भारतरहित घिरनी से होकर गुजरते है द्रव्यमान 4m के ब्लॉक को h ऊँचाई से विरामावस्था से मुक्त किया जाता है।
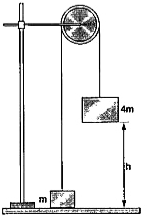
4m द्रव्यमान के ब्लॉक का क्षैतिज तल से संपर्क होने से ठीक दोनों ब्लॉक की चाल होगी02:44View Solutionचित्र 4.9 में प्रदर्शित व्यवस्था में अवितान्य डोरी से जुड़े दो ब्लॉक जिनके द्रव्यमान क्रमशः m तथा 4m है, एक भारतरहित घिरनी से होकर गुजरते है द्रव्यमान 4m के ब्लॉक को h ऊँचाई से विरामावस्था से मुक्त किया जाता है।
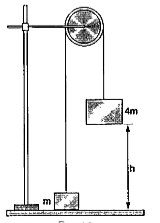
घिरनी पर गति के क्रम में कुल दाब है02:53View Solutionकिसी पतले गोलीय खोल से बाहर इसका गुरुत्वीय क्षेत्रफा तथा विभव वही होता है जैसे इसका संपूर्ण द्रव्यमान गोले के केंद्र पर केंद्रित हो। गोलीय खोल के भीतर इसका गुरुत्वीय क्षेत्र शून्य होता है जबकि विभव सभी आंतरिक बिंदुओं पर सतह पर विभव के मान के बराबर होता है।
चित्र 4.10 में प्रदर्शित M तथा 2M द्रव्यमान के दो संकेंद्रीय पतले गोलीय खोल की त्रिज्याएँ क्रमशः R तथा 2R है उभयनिष्ठ केंद्र O पर m द्रव्यमान के कण की गुरुत्वीय स्थितिज ऊर्जा है
 03:55View Solution
03:55View Solutionकिसी पतले गोलीय खोल से बाहर इसका गुरुत्वीय क्षेत्रफा तथा विभव वही होता है जैसे इसका संपूर्ण द्रव्यमान गोले के केंद्र पर केंद्रित हो। गोलीय खोल के भीतर इसका गुरुत्वीय क्षेत्र शून्य होता है जबकि विभव सभी आंतरिक बिंदुओं पर सतह पर विभव के मान के बराबर होता है।
उभयनिष्ठ केंद्र से `1.5` R दूरी पर m द्रव्यमान के कण पर क्रियाशील गुरुत्वीय बल का परिमाण04:58View Solutionकिसी पतले गोलीय खोल से बाहर इसका गुरुत्वीय क्षेत्रफा तथा विभव वही होता है जैसे इसका संपूर्ण द्रव्यमान गोले के केंद्र पर केंद्रित हो। गोलीय खोल के भीतर इसका गुरुत्वीय क्षेत्र शून्य होता है जबकि विभव सभी आंतरिक बिंदुओं पर सतह पर विभव के मान के बराबर होता है।
उभयनिष्ठ केंद्र O से 3R दूरी पर गुरुत्वीय विभव04:58View Solutionकिसी पतले गोलीय खोल से बाहर इसका गुरुत्वीय क्षेत्रफा तथा विभव वही होता है जैसे इसका संपूर्ण द्रव्यमान गोले के केंद्र पर केंद्रित हो। गोलीय खोल के भीतर इसका गुरुत्वीय क्षेत्र शून्य होता है जबकि विभव सभी आंतरिक बिंदुओं पर सतह पर विभव के मान के बराबर होता है।
उभयनिष्ठ केंद्र O से 3R दूरी पर गुरुत्वीय क्षेत्र का परिमाण04:58View Solutionभारी बोझो को उठाने के लिए क्रेनों का उपयोग होता है इसमें धातु के तारो से बनी मोती रस्सी होती है जिससे बोझ लटकाए जाते है बोझ के कारण स्थायी विरूपण न हो, इसकी सावधानी राखी जाती है इसके लिए रस्सी में विस्तार प्रत्यास्थता सीमा से कम रहना चाहिए। स्टील का पराभाव सामर्थ्य `3xx10^(8)" N m"^(-2)` है मान ले कि क्रेन के बोझ उठाने की क्षमता 10 मीट्रिक टन है।
रस्सी के अनुप्रस्थ काट का क्षेत्रफल कम-से-कम कितना होना चाहिए ?04:50View Solutionभारी बोझो को उठाने के लिए क्रेनों का उपयोग होता है इसमें धातु के तारो से बनी मोती रस्सी होती है जिससे बोझ लटकाए जाते है बोझ के कारण स्थायी विरूपण न हो, इसकी सावधानी राखी जाती है इसके लिए रस्सी में विस्तार प्रत्यास्थता सीमा से कम रहना चाहिए। स्टील का पराभाव सामर्थ्य `3xx10^(8)" N m"^(-2)` है मान ले कि क्रेन के बोझ उठाने की क्षमता 10 मीट्रिक टन है।
क्रेन की स्टील की रस्सी की मोटाई कितनी होनी चाहिए ?04:50View Solutionभारी बोझो को उठाने के लिए क्रेनों का उपयोग होता है इसमें धातु के तारो से बनी मोती रस्सी होती है जिससे बोझ लटकाए जाते है बोझ के कारण स्थायी विरूपण न हो, इसकी सावधानी राखी जाती है इसके लिए रस्सी में विस्तार प्रत्यास्थता सीमा से कम रहना चाहिए। स्टील का पराभाव सामर्थ्य `3xx10^(8)" N m"^(-2)` है मान ले कि क्रेन के बोझ उठाने की क्षमता 10 मीट्रिक टन है।
रस्सी का सामर्थ्य, लचीलापन तथा निर्माण में सुगमता को ध्यान में रखकर बोझ लटकाने के लिए04:50View Solution1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
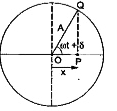
चित्र 4.11 में एक कण को अचर कोणीय चाल `omega` से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति `omegat+delta` हैं यहाँ `delta` इस कण की `t=0` पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
`x=Acos(omegat=delta)`
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
`x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"}`
तो
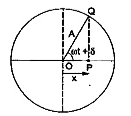
सरल आवर्त गति के आयाम या निर्देश वृत्त की त्रिज्या का मान है03:55View Solution1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
चित्र 4.11 में एक कण को अचर कोणीय चाल `omega` से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति `omegat+delta` हैं यहाँ `delta` इस कण की `t=0` पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
`x=Acos(omegat=delta)`
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
`x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"}`
तो
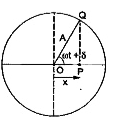
सरल आवर्त गति की कोणीय आवृत्ति या एकसमान वृत्तीय गति करते कण की कोणीय चाल है03:56View Solution1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
चित्र 4.11 में एक कण को अचर कोणीय चाल `omega` से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति `omegat+delta` हैं यहाँ `delta` इस कण की `t=0` पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
`x=Acos(omegat+delta)`
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
`x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"}`
तो
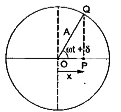
सरल आवर्त गति या एकसमान वृत्तीय गति की आवृत्ति का मान है03:41View Solution1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
चित्र 4.11 में एक कण को अचर कोणीय चाल `omega` से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति `omegat+delta` हैं यहाँ `delta` इस कण की `t=0` पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
`x=Acos(omegat=delta)`
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
`x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"}`
तो
सरल आवर्त गति का दोलन - काल या एकसमान वृत्तीय गति का परिक्रमण काल है04:20View Solution1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
चित्र 4.11 में एक कण को अचर कोणीय चाल `omega` से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति `omegat+delta` हैं यहाँ `delta` इस कण की `t=0` पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
`x=Acos(omegat=delta)`
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
`x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"}`
तो
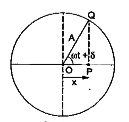
`t=1.5s` पर कण का विस्थापन होगा04:35View Solution1610 में गैलीलियो ने वृहस्पति गृह के चाकर प्रमुख चंद्रमाओं की खोज की उन्हें प्रत्येक चंद्रमा, जैसे कैलिस्ट्रो, गृह के सापेक्ष सरल आवर्त गति करता हुआ प्रतीत हुआ। वास्तव में कैलिस्ट्रो की गति एकसमान वृत्तीय गति है यदि कोई कण किसी वृत्त की परिधि पर एक समान चाल से परिक्रमण कर रहा हों तो कण से वृत्त के व्यास पर खींचे गए लंब के पाद की गति सरल आवर्त गति देती है इस वृत्त को सरल आवर्त गति का निर्देश वृत्त कहते है।
चित्र 4.11 में एक कण को अचर कोणीय चाल `omega` से A त्रिज्या के वृत्त पर गति करते हुए दर्शाया गया है। किसी समय t पर, कण की कोणीय स्थिति `omegat+delta` हैं यहाँ `delta` इस कण की `t=0` पर कोणीय स्थिति है x-अक्ष पर Q के प्रक्षेप बिंदु P की स्थिति निमांकित समीकरण से प्राप्त होती है।
`x=Acos(omegat+delta)`
जो कि सरल आवर्त गति का समीकरण है
यदि प्रक्षेप बिंदु P निम्नलिखित समीकरण के अनुसार सरल आवर्त गति करता है,
`x=(4.0m)cos{(4pi" rad s"^(-1))t+pi/3" rad"}`
तो
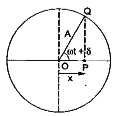
`t=1.5s` पर कण का विस्थापन होगा04:35View Solutionकिसी बिंदु पर वायुमंडलीय दाब उस बिंदु के एकांक अनुप्रस्थ काट वाले क्षेत्रफल पर उस बिंदु से वायुमंडल के शीर्ष तक की वायु के स्तंभ के भार के बराबर होता है समुद्रतल पर यह दाब `1.013xx10^(5)" Pa"` है। वास्तव में ऊँचाई के साथ वायु के घनत्व में कमी होती जाती है ऐसा ही गुरुत्वीय त्वरण g के साथ भी होता है वायुमंडलीय आवरण का विस्तार घटते दाब के साथ लगभग 100 km तक है।
समुद्रतल पर वायुमंडल का घनत्व `1.29" kg m"^(-3)` है। परिकलन की सुविधा के लिए मानब कि ऊँचाई के साथ घनत्व और गुरुत्वीय त्वरण में कोई परिवर्तन नहीं होता है गुरुत्वीय त्वरण g का मान `9.8" m s"^(-2)` और समुद्री जल का घनत्व `1.03xx10^(-3)" kg m"^(-3)` लें।
ऊँचाई के साथ वायुमंडल के घनत्व और गुरुत्वीय त्वरण में कोई परिवर्तन न हो, तो वायुमंडल का विस्तार कितनी ऊँचाई तक होगा ?01:43View Solutionकिसी बिंदु पर वायुमंडलीय दाब उस बिंदु के एकांक अनुप्रस्थ काट वाले क्षेत्रफल पर उस बिंदु से वायुमंडल के शीर्ष तक की वायु के स्तंभ के भार के बराबर होता है समुद्रतल पर यह दाब `1.013xx10^(5)" Pa"` है। वास्तव में ऊँचाई के साथ वायु के घनत्व में कमी होती जाती है ऐसा ही गुरुत्वीय त्वरण g के साथ भी होता है वायुमंडलीय आवरण का विस्तार घटते दाब के साथ लगभग 100 km तक है।
समुद्रतल पर वायुमंडल का घनत्व `1.29" kg m"^(-3)` है। परिकलन की सुविधा के लिए मानब कि ऊँचाई के साथ घनत्व और गुरुत्वीय त्वरण में कोई परिवर्तन नहीं होता है गुरुत्वीय त्वरण g का मान `9.8" m s"^(-2)` और समुद्री जल का घनत्व `1.03xx10^(-3)" kg m"^(-3)` लें।
समुद्र के नीचे 1000 m गहराई पर परम दाब कितना है ?01:43View Solutionकिसी बिंदु पर वायुमंडलीय दाब उस बिंदु के एकांक अनुप्रस्थ काट वाले क्षेत्रफल पर उस बिंदु से वायुमंडल के शीर्ष तक की वायु के स्तंभ के भार के बराबर होता है समुद्रतल पर यह दाब `1.013xx10^(5)" Pa"` है। वास्तव में ऊँचाई के साथ वायु के घनत्व में कमी होती जाती है ऐसा ही गुरुत्वीय त्वरण g के साथ भी होता है वायुमंडलीय आवरण का विस्तार घटते दाब के साथ लगभग 100 km तक है।
समुद्रतल पर वायुमंडल का घनत्व `1.29" kg m"^(-3)` है। परिकलन की सुविधा के लिए मानब कि ऊँचाई के साथ घनत्व और गुरुत्वीय त्वरण में कोई परिवर्तन नहीं होता है गुरुत्वीय त्वरण g का मान `9.8" m s"^(-2)` और समुद्री जल का घनत्व `1.03xx10^(-3)" kg m"^(-3)` लें।
उसी गहराई पर गेज दाब कितना है ?01:43View Solutionकिसी बिंदु पर वायुमंडलीय दाब उस बिंदु के एकांक अनुप्रस्थ काट वाले क्षेत्रफल पर उस बिंदु से वायुमंडल के शीर्ष तक की वायु के स्तंभ के भार के बराबर होता है समुद्रतल पर यह दाब `1.013xx10^(5)" Pa"` है। वास्तव में ऊँचाई के साथ वायु के घनत्व में कमी होती जाती है ऐसा ही गुरुत्वीय त्वरण g के साथ भी होता है वायुमंडलीय आवरण का विस्तार घटते दाब के साथ लगभग 100 km तक है।
समुद्रतल पर वायुमंडल का घनत्व `1.29" kg m"^(-3)` है। परिकलन की सुविधा के लिए मानब कि ऊँचाई के साथ घनत्व और गुरुत्वीय त्वरण में कोई परिवर्तन नहीं होता है गुरुत्वीय त्वरण g का मान `9.8" m s"^(-2)` और समुद्री जल का घनत्व `1.03xx10^(-3)" kg m"^(-3)` लें।
इस गहराई पर पनडुब्बी की `30cmxx30cm` क्षेत्रफलवाली खिड़की (जिसके आंतरिक भाग का दाब समुद्र तल पर वायुमंडलीय दाब के बराबर रखा गया है) पर आरोपित बल का आकलन कीजिए।01:43View Solutionचित्र 4.12 में एक ऐयरोफॉयल दर्शाया गया है जिसे ऐसा आकार दिया गया है ताकि जब वह वायु में होकर क्षतिजतः गति करता है तो उस पर एक ऊर्ध्वमुखी ऊर्ध्वाधर बल आरोपित हो। इसी प्रकार का बल किसी वायुयान को उड़ाता है।
किसी वायुयान में पंखो की अनुप्रस्थ काट चित्र 4.12 में दर्शाए गए ऐयरोफॉयल के समान प्रतीत होती है ऐयरोफॉयल की विशेष आकृति के कारण वेग से पीछे की ओर जाती वायु की चाल ऐयरोफॉयल के शीर्षभाग पर पेंदी की तुलना में कहीं अधिक हो जाती है बर्नूली के सिद्धांत के अनुसार इसके कारण पंखो पर उर्ध्वमुखी बल उत्पन्न होता है जो वायुयान के भार को संतुलित करता है किसी पूर्णतः भारित बोइंग विमान का संहति द्रव्यमान `3.3xx10^(5)" kg"` है। इसका कुल पंख क्षेत्रफल `490" m"^(2)` है यह एक निश्चित ऊँचाई पर `972" km h"^(-1)` की चाल से उड़ रहा है वायु का घनत्व `rho=1.2" kg m"^(-3)` है

पंख के ऊपरी तथा निचले पृष्ठों के बीच दाबांतर क्या होगा ?06:25View Solutionचित्र 4.12 में एक ऐयरोफॉयल दर्शाया गया है जिसे ऐसा आकार दिया गया है ताकि जब वह वायु में होकर क्षतिजतः गति करता है तो उस पर एक ऊर्ध्वमुखी ऊर्ध्वाधर बल आरोपित हो। इसी प्रकार का बल किसी वायुयान को उड़ाता है।
किसी वायुयान में पंखो की अनुप्रस्थ काट चित्र 4.12 में दर्शाए गए ऐयरोफॉयल के समान प्रतीत होती है ऐयरोफॉयल की विशेष आकृति के कारण वेग से पीछे की ओर जाती वायु की चाल ऐयरोफॉयल के शीर्षभाग पर पेंदी की तुलना में कहीं अधिक हो जाती है बर्नूली के सिद्धांत के अनुसार इसके कारण पंखो पर उर्ध्वमुखी बल उत्पन्न होता है जो वायुयान के भार को संतुलित करता है किसी पूर्णतः भारित बोइंग विमान का संहति द्रव्यमान `3.3xx10^(5)" kg"` है। इसका कुल पंख क्षेत्रफल `490" m"^(2)` है यह एक निश्चित ऊँचाई पर `972" km h"^(-1)` की चाल से उड़ रहा है वायु का घनत्व `rho=1.2" kg m"^(-3)` है

निचले पृष्ठों की तुलना में ऊपरी पृष्ठ पर वायु की चाल में आंशिक वृद्धि का मान क्या होगा ?07:35View Solutionकिसी वक्रित द्रव - वायु अंतरापृष्ठ के दोनों ओर दाब में अंतर होने के परिणामस्वरूप किसी पतली नली में गुरुत्व के विरुद्ध जल ऊपर उठता है लैटिन भाषा में शब्द का अर्थ है केश इसी शब्द से व्युत्पन्न हुआ एक अन्य शब्द जिसका अर्थ है केशनली अथवा केशिका। यदि कोई नली केश की भाँति पतली हो, तो उस नली में जल अधिक ऊँचाई तक ऊपर उठेगा।
एक केशनली में जल `8.0` cm ऊँचाई तक चढ़ता है यदि केशनली को उर्ध्व से `45^(@)` झुका दिया जाए, तो नली में जल-स्तंभ की ऊर्ध्वाधर ऊँचाई क्या होगी ?02:01View Solutionकिसी वक्रित द्रव - वायु अंतरापृष्ठ के दोनों ओर दाब में अंतर होने के परिणामस्वरूप किसी पतली नली में गुरुत्व के विरुद्ध जल ऊपर उठता है लैटिन भाषा में शब्द का अर्थ है केश इसी शब्द से व्युत्पन्न हुआ एक अन्य शब्द जिसका अर्थ है केशनली अथवा केशिका। यदि कोई नली केश की भाँति पतली हो, तो उस नली में जल अधिक ऊँचाई तक ऊपर उठेगा।
जल नली की कितनी लम्बाई को घेरेगा ?07:42View Solutionकिसी वक्रित द्रव - वायु अंतरापृष्ठ के दोनों ओर दाब में अंतर होने के परिणामस्वरूप किसी पतली नली में गुरुत्व के विरुद्ध जल ऊपर उठता है लैटिन भाषा में शब्द का अर्थ है केश इसी शब्द से व्युत्पन्न हुआ एक अन्य शब्द जिसका अर्थ है केशनली अथवा केशिका। यदि कोई नली केश की भाँति पतली हो, तो उस नली में जल अधिक ऊँचाई तक ऊपर उठेगा।
यदि नली को जल में इस तरह ऊर्ध्वाधर खड़ा किया जाए की उसकी `5.0` cm लम्बाई ही जल की सतह के ऊपर रहे तो अब जल की क्या स्थिति होगी ?03:00View Solutionकिसी गैस (जैसे हवा) में किसी द्रव के बुलबुले (जैसे साबुन का बुलबुला) के भीतर दाब - आधिक्य
`Deltap=(4gamma)/(R)`
जबकि किसी द्रव के भीतर द्रव के बुलबुले के भीतर दाब - आधिक्य
`Deltap=(2gamma)/(R)`,
जहाँ `gamma` द्रव - गैस अंतरापृष्ठ का पृष्ठ - तनाव तथा R बुलबुले की त्रिज्या है।
`2.00` mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ठ से `8.00` cm नीचे तक डुबोया जाता है और नली के जल में डूबे सिरे पर अर्धगोलिय बुलबुला फुलाया जाता है प्रयोग के ताप पर जल का पृष्ठ - तनाव `7.28xx10^(-2)" N m"^(-1)` है जल का घनत्व `=1000" kg/m"^(-3)`, वायुमंडलीय दाब `1.013xx10^(5)" Pa"` तथा `g=9.80" m s"^(-2)`.
द्रव में गैस के बुलबुले के लिए द्रव-गैस अंतरापृष्ठ कितने है ?05:40View Solutionकिसी गैस (जैसे हवा) में किसी द्रव के बुलबुले (जैसे साबुन का बुलबुला) के भीतर दाब - आधिक्य
`Deltap=(4gamma)/(R)`
जबकि किसी द्रव के भीतर द्रव के बुलबुले के भीतर दाब - आधिक्य
`Deltap=(2gamma)/(R)`,
जहाँ `gamma` द्रव - गैस अंतरापृष्ठ का पृष्ठ - तनाव तथा R बुलबुले की त्रिज्या है।
`2.00` mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ठ से `8.00` cm नीचे तक डुबोया जाता है और नली के जल में डूबे सिरे पर अर्धगोलिय बुलबुला फुलाया जाता है प्रयोग के ताप पर जल का पृष्ठ - तनाव `7.28xx10^(-2)" N m"^(-1)` है जल का घनत्व `=1000" kg/m"^(-3)`, वायुमंडलीय दाब `1.013xx10^(5)" Pa"` तथा `g=9.80" m s"^(-2)`.
गैस में द्रव के बुलबुले (जैसे साबुन का बुलबुला) द्रव - गैस अंतरापृष्ठ कितने है ?05:40View Solutionकिसी गैस (जैसे हवा) में किसी द्रव के बुलबुले (जैसे साबुन का बुलबुला) के भीतर दाब - आधिक्य
`Deltap=(4gamma)/(R)`
जबकि किसी द्रव के भीतर द्रव के बुलबुले के भीतर दाब - आधिक्य
`Deltap=(2gamma)/(R)`,
जहाँ `gamma` द्रव - गैस अंतरापृष्ठ का पृष्ठ - तनाव तथा R बुलबुले की त्रिज्या है।
`2.00` mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ठ से `8.00` cm नीचे तक डुबोया जाता है और नली के जल में डूबे सिरे पर अर्धगोलिय बुलबुला फुलाया जाता है प्रयोग के ताप पर जल का पृष्ठ - तनाव `7.28xx10^(-2)" N m"^(-1)` है जल का घनत्व `=1000" kg/m"^(-3)`, वायुमंडलीय दाब `1.013xx10^(5)" Pa"` तथा `g=9.80" m s"^(-2)`.
नली के जल में डूबे सिरे पर अर्धगोलीय बुलबुला के बाहर दाब क्या होगा ?05:40View Solutionकिसी गैस (जैसे हवा) में किसी द्रव के बुलबुले (जैसे साबुन का बुलबुला) के भीतर दाब - आधिक्य
`Deltap=(4gamma)/(R)`
जबकि किसी द्रव के भीतर द्रव के बुलबुले के भीतर दाब - आधिक्य
`Deltap=(2gamma)/(R)`,
जहाँ `gamma` द्रव - गैस अंतरापृष्ठ का पृष्ठ - तनाव तथा R बुलबुले की त्रिज्या है।
`2.00` mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ठ से `8.00` cm नीचे तक डुबोया जाता है और नली के जल में डूबे सिरे पर अर्धगोलिय बुलबुला फुलाया जाता है प्रयोग के ताप पर जल का पृष्ठ - तनाव `7.28xx10^(-2)" N m"^(-1)` है जल का घनत्व `=1000" kg/m"^(-3)`, वायुमंडलीय दाब `1.013xx10^(5)" Pa"` तथा `g=9.80" m s"^(-2)`.
बुलबुले के अंदर दाब - आधिक्य का मान क्या होगा ?05:40View Solutionकिसी गैस (जैसे हवा) में किसी द्रव के बुलबुले (जैसे साबुन का बुलबुला) के भीतर दाब - आधिक्य
`Deltap=(4gamma)/(R)`
जबकि किसी द्रव के भीतर द्रव के बुलबुले के भीतर दाब - आधिक्य
`Deltap=(2gamma)/(R)`,
जहाँ `gamma` द्रव - गैस अंतरापृष्ठ का पृष्ठ - तनाव तथा R बुलबुले की त्रिज्या है।
`2.00` mm व्यास की किसी केशनली का निचला सिरा बीकर में भरे जल के पृष्ठ से `8.00` cm नीचे तक डुबोया जाता है और नली के जल में डूबे सिरे पर अर्धगोलिय बुलबुला फुलाया जाता है प्रयोग के ताप पर जल का पृष्ठ - तनाव `7.28xx10^(-2)" N m"^(-1)` है जल का घनत्व `=1000" kg/m"^(-3)`, वायुमंडलीय दाब `1.013xx10^(5)" Pa"` तथा `g=9.80" m s"^(-2)`.
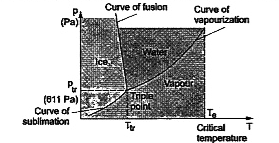
नली के जल में डूबे सिरे पर अर्धगोलीय बुलबुला के अंदर दाब क्या होगा ?05:40View Solutionp-V समताप रेखा से संबंधित सूचना को सारांशित करने के लिए दाब (p-T) प्रावस्था आरेख p-T समतल को ठोस भाग, वाष्प भाग एवं द्रव भाग में विभाजित करता है ये भाग उन वक्रो से पृथक रहते जो ठोस - द्रव साम्यावस्था (गलन), द्रव - वाष्प
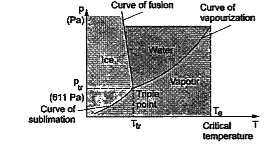
साम्यावस्था (क्वथन) तथा ठोस - वाष्प साम्यावस्था (ऊर्ध्वपातन) को व्यक्त करते है तीनों वक्र त्रिक बिंदु (ठोस -द्रव-वाष्प साम्यावस्था) पर मिलते है जल के लिए (p-T) आरेख चित्र 4.13 में दर्शाया गया है।
जल के गलनांक पर दाब में वृद्धि का क्या प्रभाव होता है ?02:38View Solutionp-V समताप रेखा से संबंधित सूचना को सारांशित करने के लिए दाब (p-T) प्रावस्था आरेख p-T समतल को ठोस भाग, वाष्प भाग एवं द्रव भाग में विभाजित करता है ये भाग उन वक्रो से पृथक रहते जो ठोस - द्रव साम्यावस्था (गलन), द्रव - वाष्प
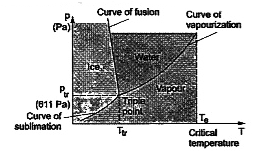
साम्यावस्था (क्वथन) तथा ठोस - वाष्प साम्यावस्था (ऊर्ध्वपातन) को व्यक्त करते है तीनों वक्र त्रिक बिंदु (ठोस -द्रव-वाष्प साम्यावस्था) पर मिलते है जल के लिए (p-T) आरेख चित्र 4.13 में दर्शाया गया है।
जल के क्वथनांक पर दाब में वृद्धि का क्या प्रभाव होता है ?02:58View Solutionp-V समताप रेखा से संबंधित सूचना को सारांशित करने के लिए दाब (p-T) प्रावस्था आरेख p-T समतल को ठोस भाग, वाष्प भाग एवं द्रव भाग में विभाजित करता है ये भाग उन वक्रो से पृथक रहते जो ठोस - द्रव साम्यावस्था (गलन), द्रव - वाष्प
साम्यावस्था (क्वथन) तथा ठोस - वाष्प साम्यावस्था (ऊर्ध्वपातन) को व्यक्त करते है तीनों वक्र त्रिक बिंदु (ठोस -द्रव-वाष्प साम्यावस्था) पर मिलते है जल के लिए (p-T) आरेख चित्र 4.13 में दर्शाया गया है।
वह कौन - सा ताप है जिससे अधिक ताप पर भाप पानी में संघनित नहीं होती यघपि यह अत्यधिक दाब से (संतापीय विधि से) संघनित की जाती है02:06View Solutionp-V समताप रेखा से संबंधित सूचना को सारांशित करने के लिए दाब (p-T) प्रावस्था आरेख p-T समतल को ठोस भाग, वाष्प भाग एवं द्रव भाग में विभाजित करता है ये भाग उन वक्रो से पृथक रहते जो ठोस - द्रव साम्यावस्था (गलन), द्रव - वाष्प

साम्यावस्था (क्वथन) तथा ठोस - वाष्प साम्यावस्था (ऊर्ध्वपातन) को व्यक्त करते है तीनों वक्र त्रिक बिंदु (ठोस -द्रव-वाष्प साम्यावस्था) पर मिलते है जल के लिए (p-T) आरेख चित्र 4.13 में दर्शाया गया है।
जल के त्रिक बिंदु का दाब क्या है01:42View Solutionp-V समताप रेखा से संबंधित सूचना को सारांशित करने के लिए दाब (p-T) प्रावस्था आरेख p-T समतल को ठोस भाग, वाष्प भाग एवं द्रव भाग में विभाजित करता है ये भाग उन वक्रो से पृथक रहते जो ठोस - द्रव साम्यावस्था (गलन), द्रव - वाष्प
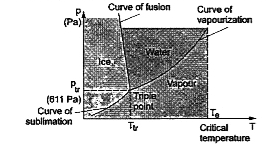
साम्यावस्था (क्वथन) तथा ठोस - वाष्प साम्यावस्था (ऊर्ध्वपातन) को व्यक्त करते है तीनों वक्र त्रिक बिंदु (ठोस -द्रव-वाष्प साम्यावस्था) पर मिलते है जल के लिए (p-T) आरेख चित्र 4.13 में दर्शाया गया है।
क्या होता है यदि 450 Pa दाब पर जल के वाष्प को `0" "^(@)C` तक ठंडा किया जाता है ?03:47View Solutionलोहे की एक गेंद 100 g की गेंद `10.0` m की ऊँचाई से गिरती है तथा पृथ्वी से टकराकर पुनः `1.0` m ऊँचाई तक उछल जाती है गेंद के पदार्थ की विशिष्ट ऊष्मा-धारिता `500" J kg"^(-1)" K"^(-1)` है मान लें कि गेंद की यांत्रिक ऊर्जा का क्षय हुआ अंश पूर्णतः गेंद में ही रह जाता है।
गेंद पर कितना कार्य किया गया ?06:41View Solutionलोहे की एक गेंद 100 g की गेंद `10.0` m की ऊँचाई से गिरती है तथा पृथ्वी से टकराकर पुनः `1.0` m ऊँचाई तक उछल जाती है गेंद के पदार्थ की विशिष्ट ऊष्मा-धारिता `500" J kg"^(-1)" K"^(-1)` है मान लें कि गेंद की यांत्रिक ऊर्जा का क्षय हुआ अंश पूर्णतः गेंद में ही रह जाता है।
गेंद की आंतरिक ऊर्जा में क्या परिवर्तन हुआ ?06:41View Solutionलोहे की एक गेंद 100 g की गेंद `10.0` m की ऊँचाई से गिरती है तथा पृथ्वी से टकराकर पुनः `1.0` m ऊँचाई तक उछल जाती है गेंद के पदार्थ की विशिष्ट ऊष्मा-धारिता `500" J kg"^(-1)" K"^(-1)` है मान लें कि गेंद की यांत्रिक ऊर्जा का क्षय हुआ अंश पूर्णतः गेंद में ही रह जाता है।
टकराने पर गेंद के ताप में कितनी वृद्धि हुई ?06:41View Solutionकोई तरंग, चारे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
संचरण स्थिरांक का SI मात्रक क्या है ?02:36View Solutionकोई तरंग, चारे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
तरंग की कोणीय आवृत्ति का SI मात्रक क्या है ?02:21View Solutionकोई तरंग, चारे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
तरंग का आयाम क्या है ?02:51View Solutionकोई तरंग, चारे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
तरंग का तरंगदैर्घ्य का मान कितना है ?03:59View Solutionकोई तरंग, चारे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
तरंग की आवृत्ति क्या है ?02:48View Solutionकोई तरंग, चाहे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
तरंग का आवर्तकाल का मान कितना है ?03:33View Solutionकोई तरंग, चाहे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
दूरी `x=30` cm तथा समय `t=20` s पर तरंग का विस्थापन y क्या होगा ?06:05View Solutionकोई तरंग, चारे वह अनुप्रस्थ हो अथवा अनुदैर्घ्य, प्रगामी तरंग कहलाती है, यदि वह माध्यम के एक बिंदु से दूसरे बिंदु तक गमन करती है। केवल तरंग अथवा विक्षोभ ही एक सिरे से दूसरे सिरे तक गमन करता है वह द्रव्य जिससे तरंग संचारित होती है गति नहीं करता। अनुप्रस्थ तरंगो में कणो की गति तरंग संचरण की दिशा के लंबवत होती है।
किसी माध्यम में तरंग गति के संचरण (तथा माध्यम के किसी अवयव की गति) के विवरण के लिए हमें किसी ऐसे फलां की आवश्यकता होती है जो उस तरंग की आकृति का समय के प्रत्येक क्षण पर सम्पूर्ण विवरण देता हो।
मान लिया कि समय t तथा स्थिति x पर डोरी के किसी अवयव का अनुप्रस्थ विस्थापन y(x,t) है जब तरंग डोरी के अनुवर्ती अवयवों की ओर बढ़ती जाती है तो वे अवयव y-अक्ष के समांतर दोलन करने लगते है तब हम किसी समय t पर स्थिति x पर अवस्थित अवयव के विस्थापन y को इस प्रकार व्यक्त करते है
`y(x,t)=asin(kx-omegat)`,
जहाँ `k=(2pi)/(lamda)` और`omega=(2pi)/(T)=2pif`.
k को संचरण स्थिरांक अथवा कोणीय तरंग संख्या और `omega` को तरंग की कोणीय आवृत्ति कहते है।
किसी डोरी के अनुदिश गमन करती तरंग का विवरण इस प्रकार दिया गया है -
`y(x,t)=(0.005" m")sin{(80.0" rad/m")x-(3.0" rad/s")t}`
तरंग की चाल का मान क्या होगा ?07:20View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter बोध - संबद्ध प्रकार के प्रश्न of DAS GUPTA of Class 11