Complete Solutions to Level 1 Subjective of chapter LAWS OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF THERMODYNAMICS |
| DC PANDEY | Level 1 Subjective |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
How many moles of helium at temperature 300K and 1.00 atm pressure are needed to make the internal energy of the gas 100J?
View SolutionShow how internal energy U varies with T in isochoric, isobaric and adiabatic process?
View SolutionA system is taken around the cycle shown in figure from state a to state b and then back to state a. The absolute value of the heat transfer during one cyle is 7200J. (a) Does the system absorb or liberate heat when it goes around the cycle in the direction shown in figure? (b) What is the work W done by the system in one cycle? (c) If the system goes around the cycle in a counter-clock wise direction, does it absorb or liberate heat in one cycle? What is the magnitude of the heat absorbed or liberated in one counter-clockwise cycle?
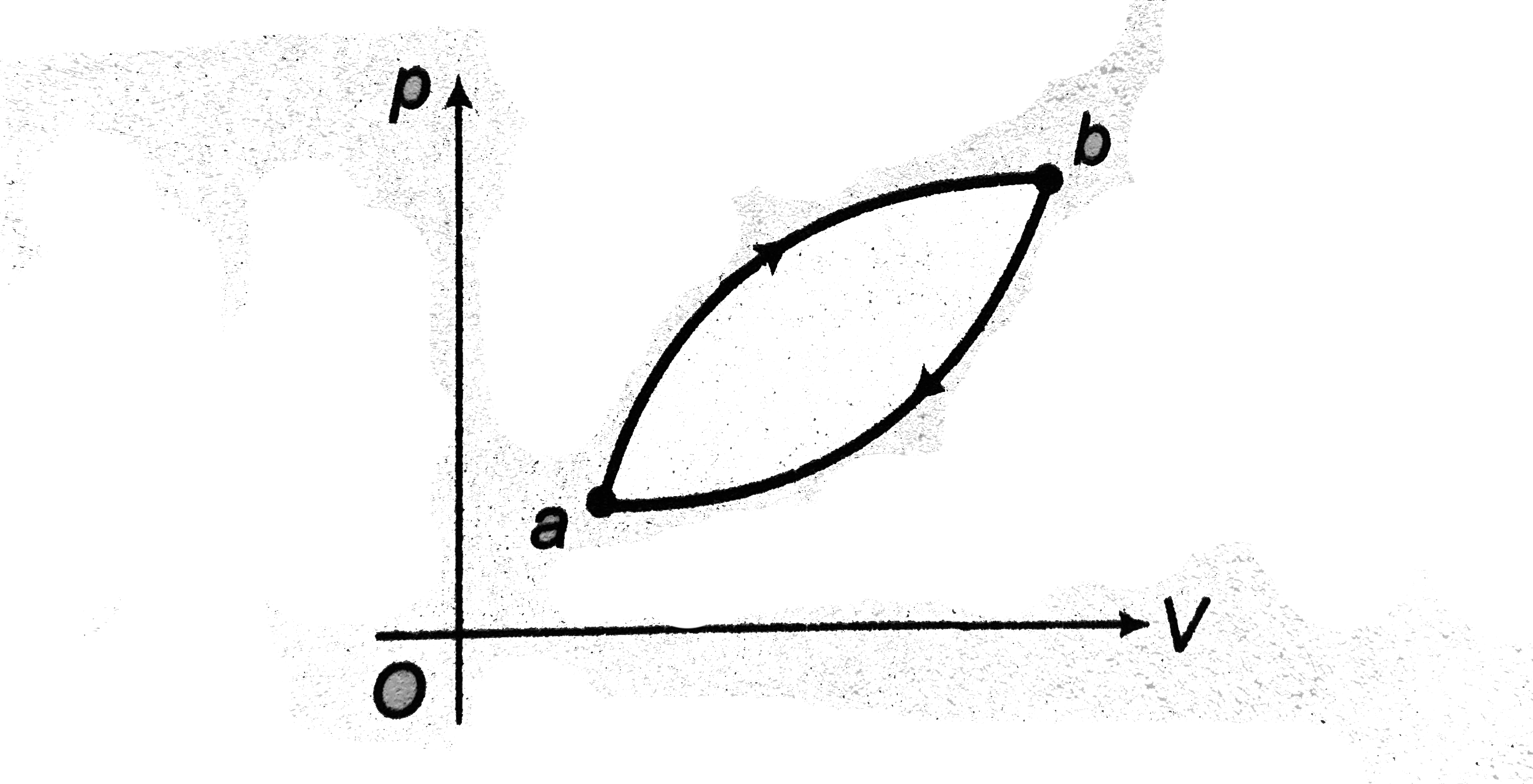
View SolutionFor the thermodynamic cycle shown in figure find (a) net output work of the gas during the cycle, (b) net heat flow into the gas per cycle.

View SolutionA thermodynamic system undergoes a cyclic process as shown in figure. The cycle consists of two closed loops, loop I and loop II. (a) Over one complete cycle, does the system do positive or negative work? (b) In each of loops I and II, is the net work done by the system positive or negative? (c) Over one complete cycle, does heat flow into or out of the system? (d) In each of loops I and II, does heat flow into or out of the system?

View SolutionA gas undergoes the cycle shown in figure. The cycle is repeated 100 times per minute. Determine the power generated.

View SolutionOne mole of an ideal monoatomic gas is initially at 300K. Find the final temperature if 200J of heat are added as follows:
(a) at constant volume (b) at constant pressure.
View SolutionA closed vessel 10L in volume contains a diatomic gas under a pressure of `10^5N//m^2`. What amount of heat should be imparted to the gas to increase the pressure in the vessel five times?
View SolutionOne mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.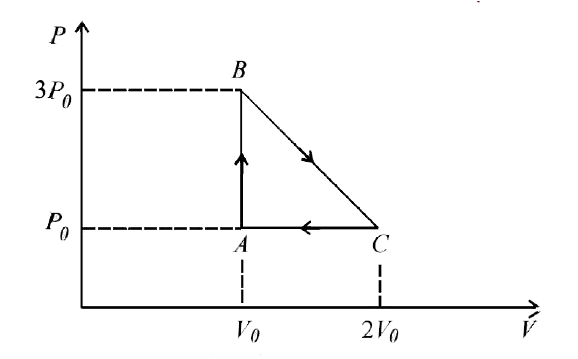
View SolutionA diatomic ideal gas is heated at constant volume until its pressure becomes three times. It is again heated at constant pressure until its volume is doubled. Find the molar heat capacity for the whole process.
View SolutionTwo moles of a certain gas at a temperature `T_0=300K` were cooled isochorically so that the pressure of the gas got reduced 2 times. Then as a result of isobaric process, the gas is allowed to expand till its temperature got back to the initial value. Find the total amount of heat absorbed by gas in this process.
View SolutionFive moles of an ideal monoatomic gas with an initial temperature of `127^@C` expand and in the process absorb 1200J of heat and do 2100J of work. What is the final temperature of the gas?
View SolutionFind the change in the internal energy of `2 kg` of water as it heated from `0^(0)C to 4^(0)C`. The specific heat capacity of water is `4200 J kg^(-1) K^(-1)` and its densities at `0^(0)C` and `4^(0)C` are `999.9 kg m^(-3)` and `1000 kg m^(-3)` respectively. atmospheric pressure `=10^(5)` Pa.
View SolutionCalculate the increase in the internal energy of `10 g` of water when it is heated from `0^(0)C to 100^(0)C` and converted into steam at `100 kPa`. The density of steam `=0.6 kg m^(-3)`, specific heat capacity of water `=4200 J//kgC` ,latent heat of vaporization of water `=2.25xx10^6 J kg^(-1)`
View SolutionOne gram of water `(1 cm^3)` becomes `1671 cm^3` of steam when boiled at a constant pressure of 1 atm `(1.013xx10^5Pa)`. The heat of vaporization at this pressure is `L_v=2.256xx10^6J//kg`. Compute (a) the work done by the water when it vaporizes and (b) its increase in internal energy.
View SolutionA gas in a cyclinder is held at a constant pressure of `2.30xx10^5 Pa` and is cooled and compressed from `1.70m^3` to `1.20m^3`. The internal energy of the gas decreases by `1.40xx10^5J`. (a) Find the work done by the gas. (b) Find the absolute value `|Q|` of the heat flow into or out of the gas and state the direction of the heat flow. (c) Does it matter whether or not the gas is ideal? Why or why not?
View Solutionp-V diagram of an ideal gas for a process ABC is as shown in the figure.
(a) Find total heat absorbed or released by the gas during the process ABC.
(b) Change in internal energy of the gas during the process ABC.
(c) Plot pressure versus density graph of the gas for the process ABC.
View SolutionIn the given graph, an ideal gas changes its state from A to C by two paths ABC and AC.
(a) Find the path along which work done is less.
(b) The internal energy of gas at A is 10J and the amount of heat supplied in path AC is 200J. Calculate the internal energy of gas at C.
(c) The internal energy of gas at state B is 20J. Find the amount of heat supplied to the gas to go from A to B.
View SolutionWhen a gas expands along AB, it does 500J of work and absorbs 250 J of heat. When the gas expands along AC, it does 700J of work and absorbs 300J of heat.
(a) How much heat does the gas exchange along Bc?
(b) When the gas makes the transition from C to A along CDA, 800J of work are done on it from C to D. How much heat does it exchange along CDA?

View SolutionA 1.0 kg bar of copper is heated at atmospheric pressure `(1.01xx10^5N//m^2)`. If its temperature increases from `20^@C` to `50^@C`, calculate the change in its internal energy. `alpha=7.0xx10^-6//^@C`, `rho=8.92xx10^3kg//m^3` and `c=387J//kg-^@C`.
View SolutionOne mole of an ideal monoatomic gas occupies a volume of `1.0xx10^-2m^3` at a pressure of `2.0xx10^5N//m^2`.
(a) What is the temperature of tha gas?
(b) The gas undergoes an adiabatic compression until its volume is decreased to `5.0xx10^-3m^3`. What is the new gas temperature?
(c) How much work is done on the gas during the compression?
(d) What is the change in the intenal energy of the gas?
View SolutionA bullet of mass 10g travelling horizontally at `200m//s` strikes and embeds in a pendulum bob of mass 2.0 kg.
(a) How much mechanical energy is dissipated in the collision?
(b) Assuming that `C_v` for the bob plus bullet is 3R, calculate the temperature increase of the system due to the collision. Take the molecular mass of the system to be `200g//mol.`
View SolutionAn ideal gas is carried through a thermodynamic cycle consisting of two isobaric and two isothermal processes as shown in figure. Show that the net work done in the entire cycle is given by the equation. `W_(n et)=p_1(V_2-V_1) In(p_2)/(p_1)`

View SolutionAn ideal gas is enclosed in a cyclinder with a movable piston on top. The piston has mass of 8000g and an area of `5.00cm^2` and is free to slide up and down, keeping the pressure of the gas constant. How much work is done as the temperature of `0.200mol` of the gas is raised from `200^@C` to `300^@C`?
View Solution
Level 1 Subjective questions and complete solutions for chapter LAWS OF THERMODYNAMICS of DC PANDEY ENGLISH of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS LAWS OF THERMODYNAMICS
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Exercise 21.1
- Exercise 21.2
- Exercise 21.3
- Exercise 21.4
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Objective Questions
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Passage I
- Level 2 Passage II
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Example