Complete Solutions to C Comprehension Type Questions of chapter WORK, POWER AND ENERGY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, POWER AND ENERGY |
| DC PANDEY MASTER PROBLEM PACKAGE | C Comprehension Type Questions |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
A ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

Let h be the maximum height from ground reached by ball after leaving track at B. Then,
View SolutionA ball is released from point A as shown in figure. The ball leaves the track at B. All surfaces are smooth.

If track makes an angle `30^(@)` with horizontal at B, then maximum height attained by ball will be
View SolutionIn the figure shown, upper block is given a velocity of `6 m//s` and lower block. `3 m//s`. When relative motion between them is stopped

View SolutionIn the figure shown, upper block is given a velocity of `6 m//s` and lower block. `3 m//s`. When relative motion between them is stopped

View SolutionA ball is released from the bottom of a tank filled with water up to 2m. On reaching the top its kinetic energy is found to be 16 J. Mass of the ball is 2 kg.
Ignoring the viscosity, let `W_(1)` be the work done by upthrust and `W_(2)` the work done by gravity, then `(g = 10 m//s^(2))`

View SolutionA ball is released from the bottom of a tank filled with water up to 2m. On reaching the top its kinetic energy is found to be 16 J. Mass of the ball is 2 kg.
Density of the ball in `(kg)/(m^(3))` is

View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is `10 N//m`.
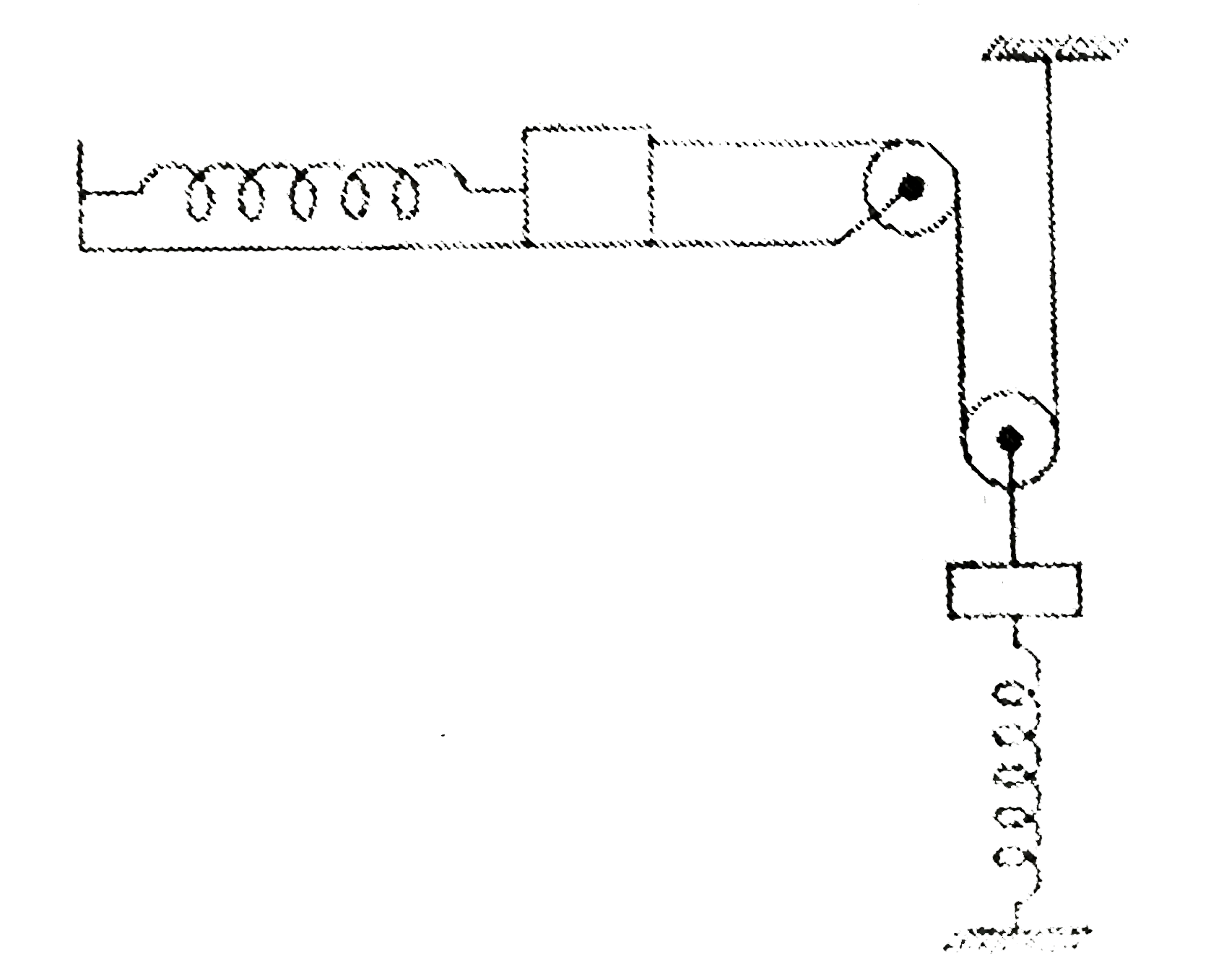
Extension of horizontal spring in equilibrium is
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is `10 N//m`.
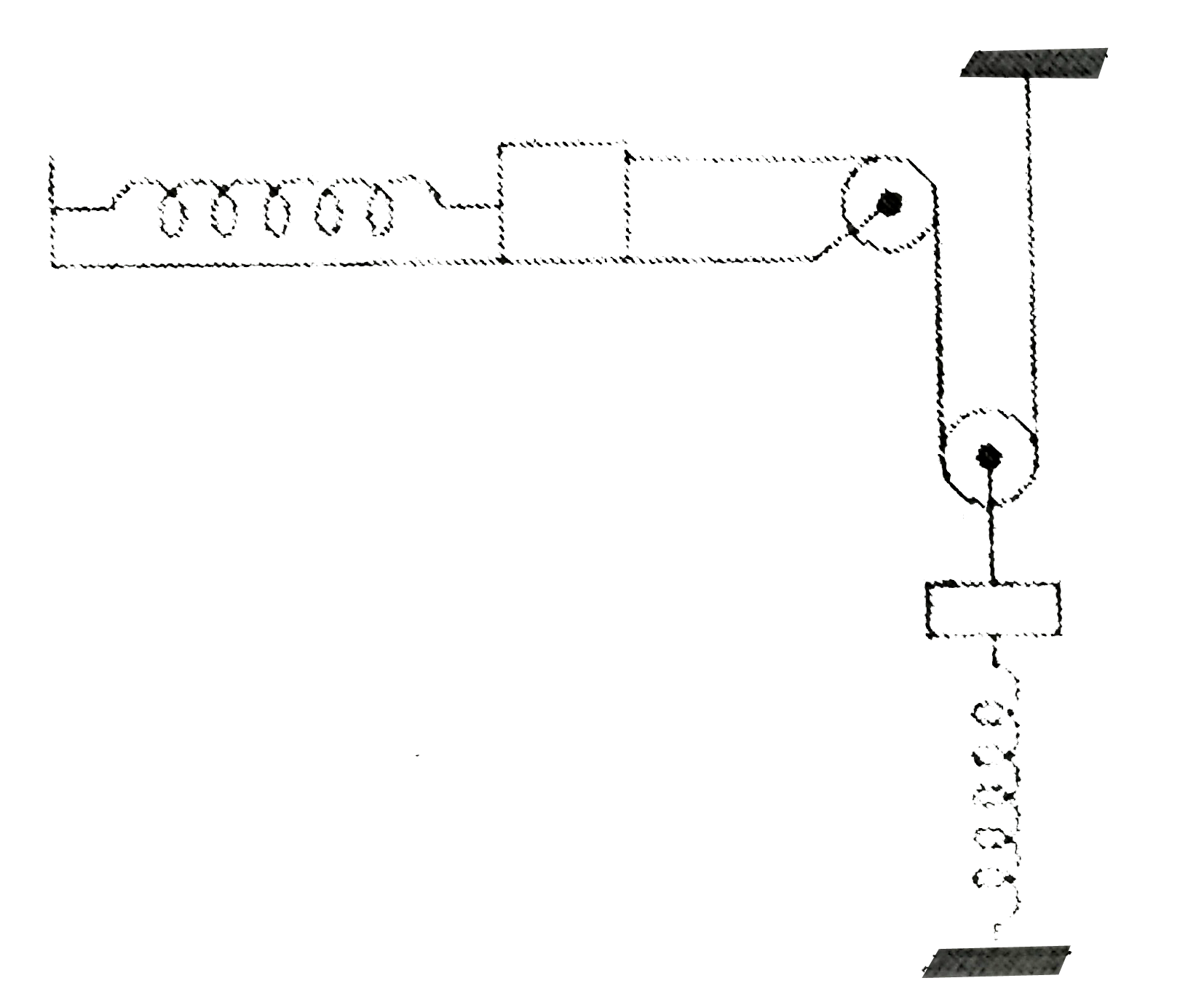
In the equilibrium position, speed of the block placed horizontally is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given by
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using `F = -(dU)/(dr)`. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : `U(r )=(A)/(r^(2))-(B)/(r )` where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is `E=-(3B^(2))/(16A)`, and it is known that the motion is radial only then the velocity is zero at
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
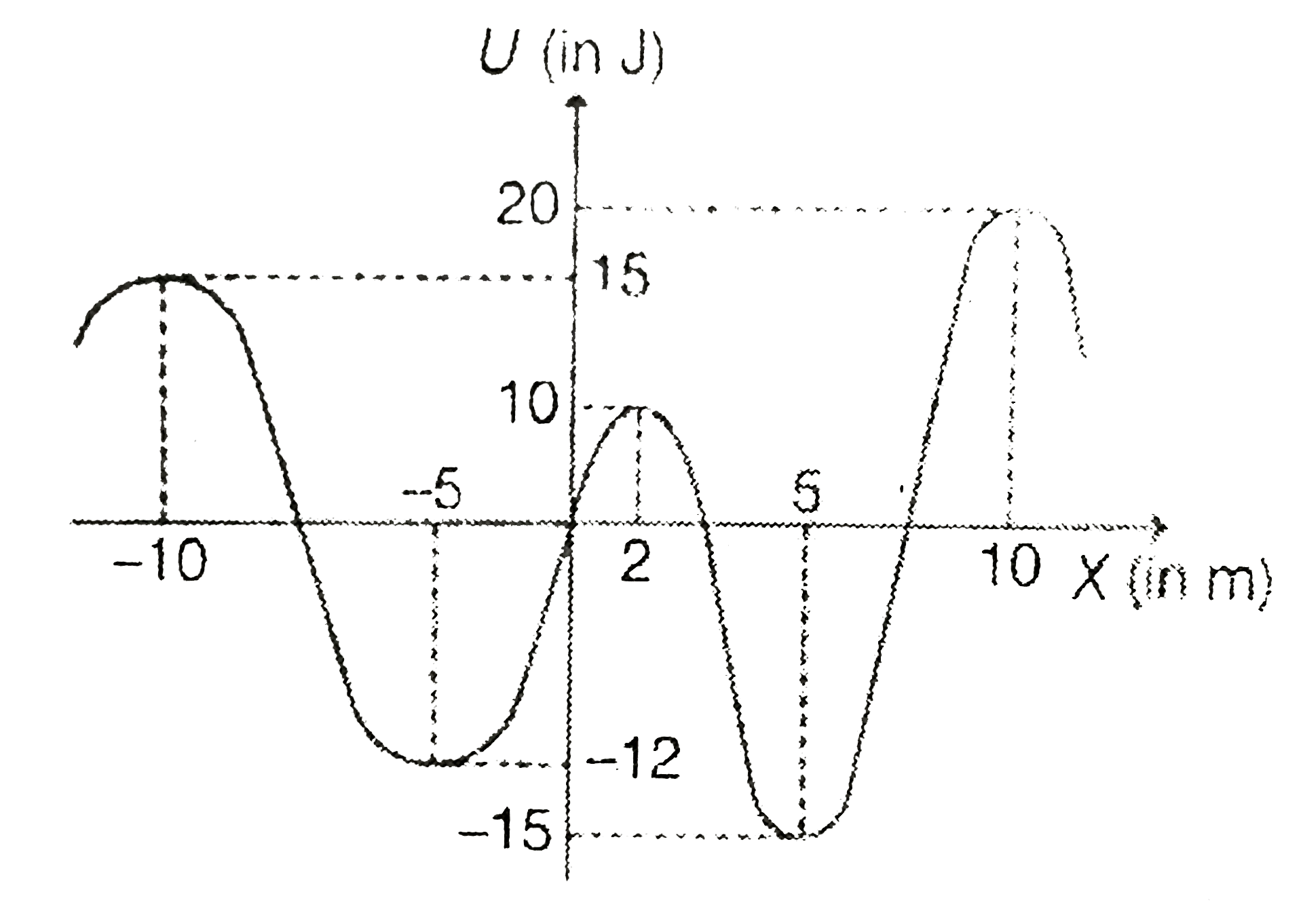
If the particle is released at the origin, then
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
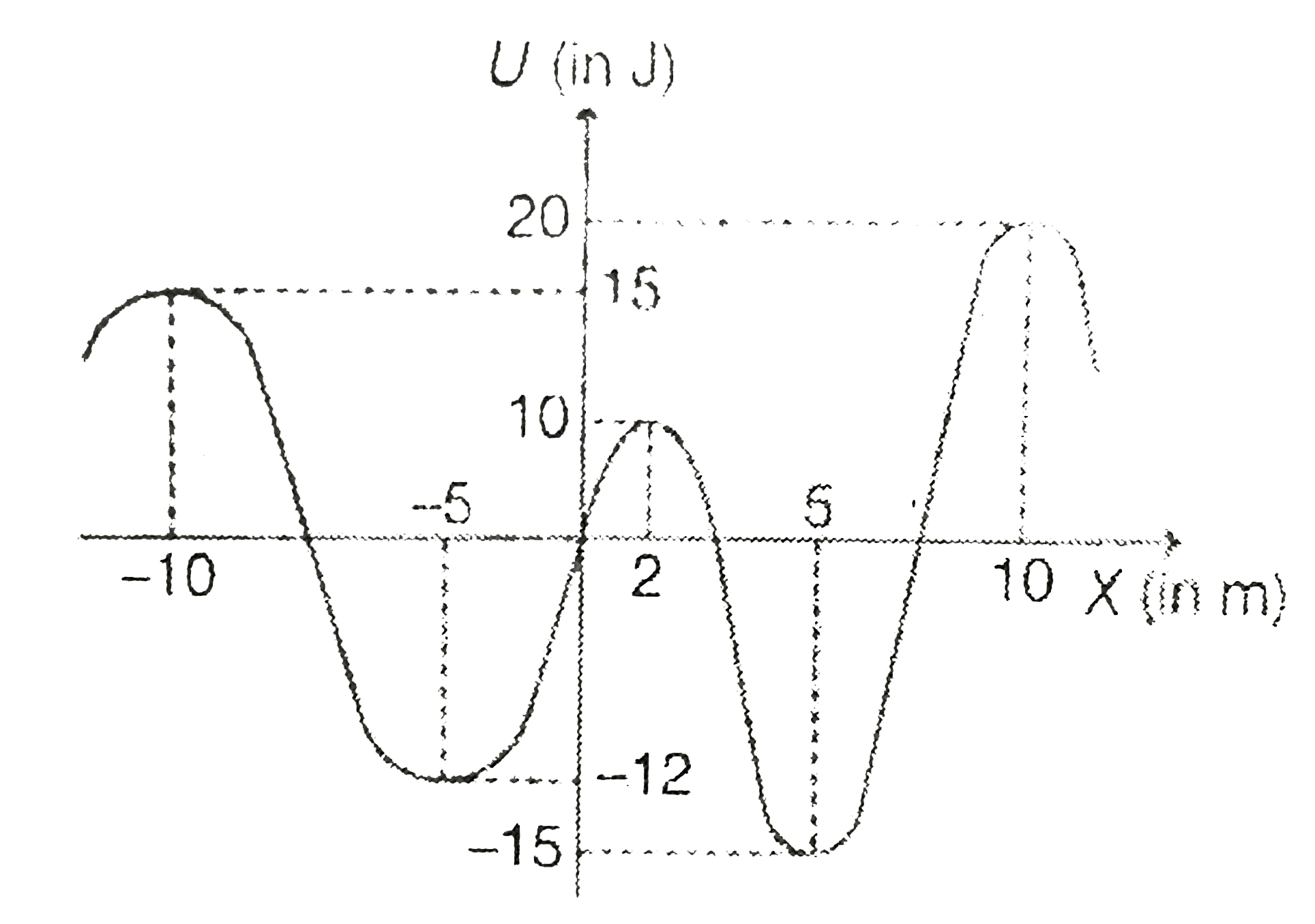
If the particle is released at `x = 2 + Delta` where `Delta rarr 0` (it is positive), then its maximum speed in subsequent motion will be
View SolutionIn the figure the variation of potential energy of a particle of mass `m = 2kg` is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
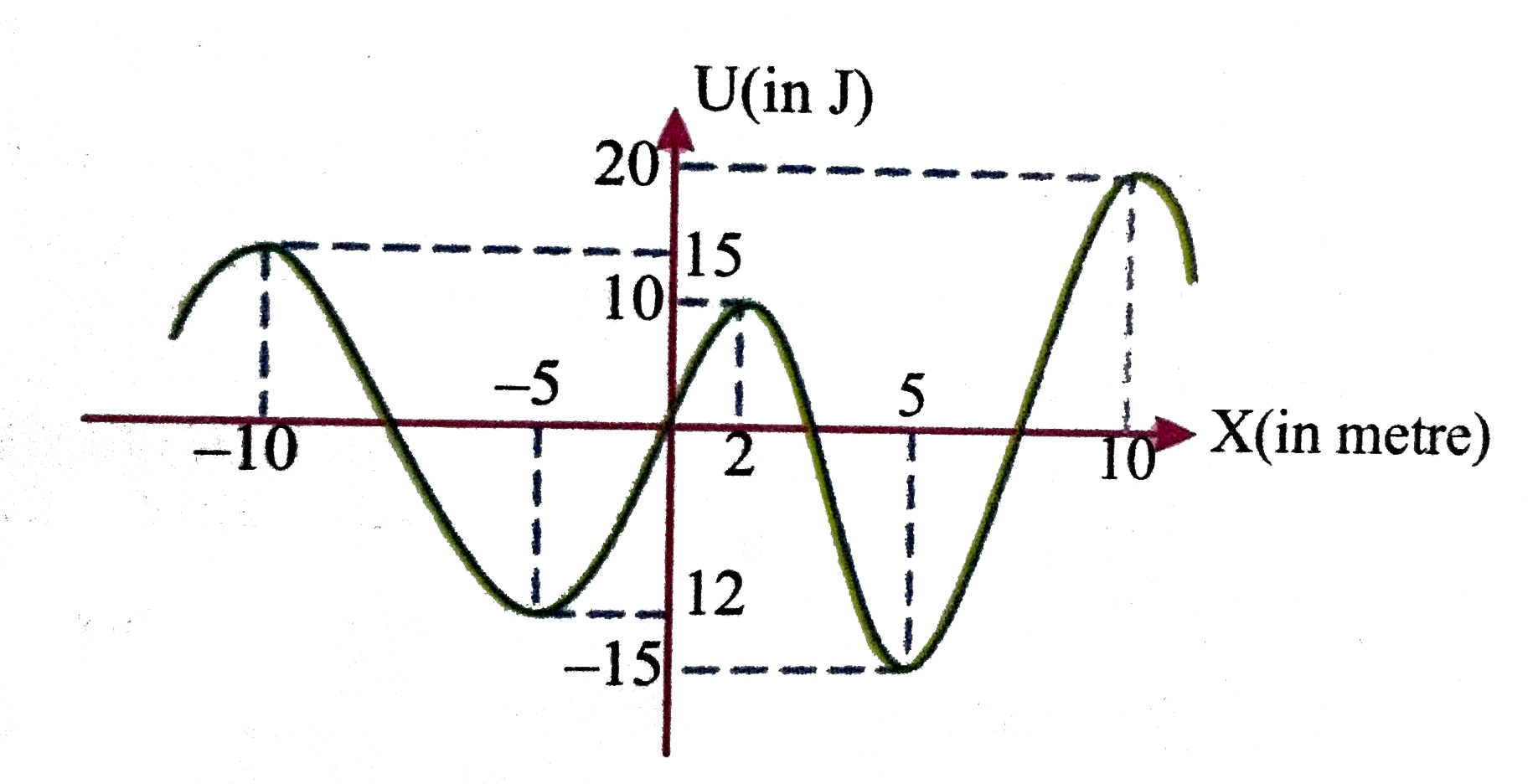
`x = - 5m` and `x = 10 m` position of the particle are respectively of
View SolutionA block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed `20 m//sec` towards right at all time.
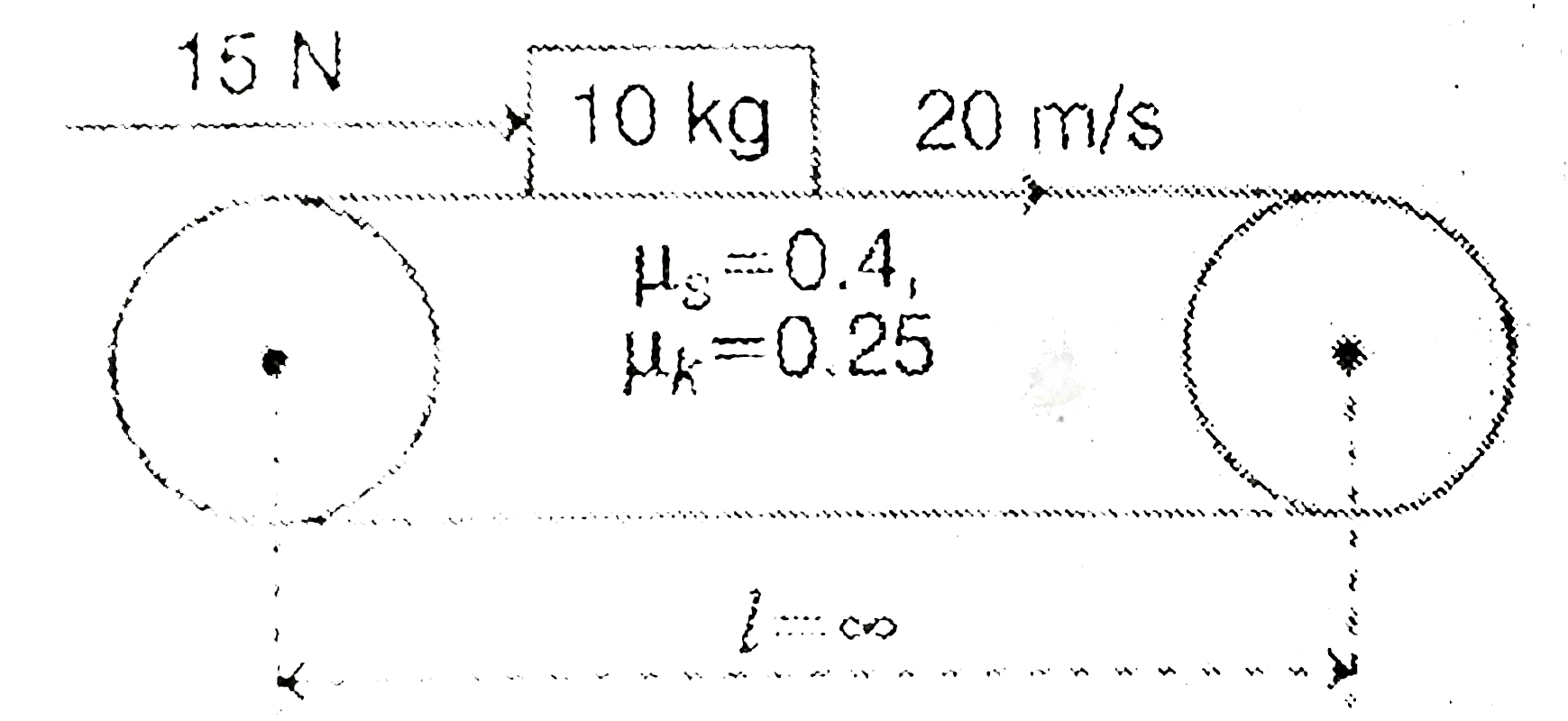
A constant force of magnitude 15 N is applied on the block continuously during its motion.
The nature of friction acting on the block of mass 10 kg during its motion is
View SolutionA block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed `20 m//sec` towards right at all time.

A constant force of magnitude 15 N is applied on the block continuously during its motion.
Work done by the kinetic friction on the block of mass 10 kg is
View SolutionA block of mass 10 kg is put gently on a belt-conveyor system of infinite length at t = 0, which is moving with constant speed `20 m//sec` towards right at all time.
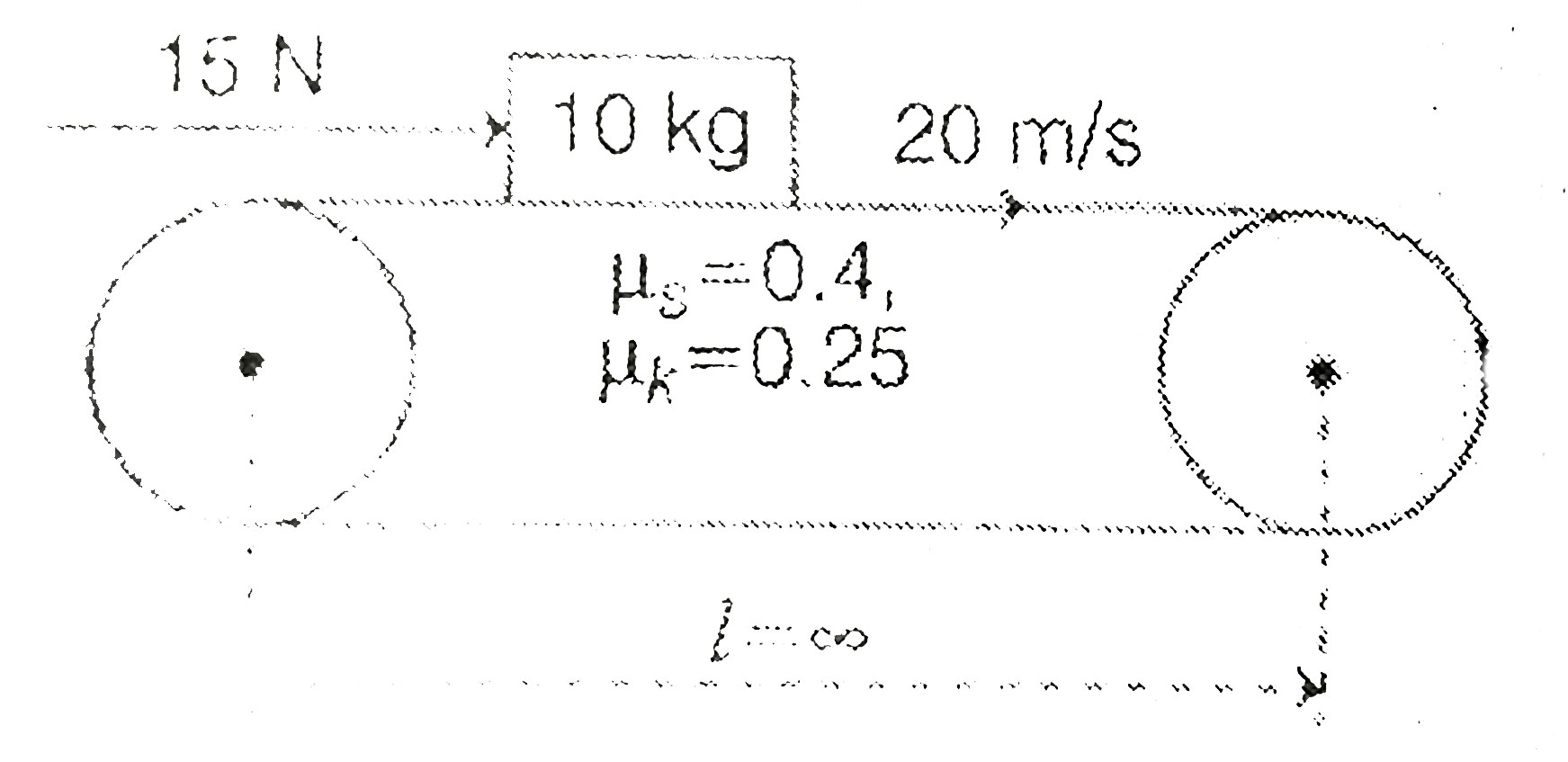
A constant force of magnitude 15 N is applied on the block continuously during its motion.
The magnitude of acceleration of the block of mass 10 kg at t = 6s is
View Solution
C Comprehension Type Questions questions and complete solutions for chapter WORK, POWER AND ENERGY of DC PANDEY PHYSICS (HINGLISH) of Class 11