Complete Solutions to Comprehension of chapter PROPERTIES OF MATTER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROPERTIES OF MATTER |
| DC PANDEY MASTER PROBLEM PACKAGE | Comprehension |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
_E01_173_Q01.png)
In a U-tube if different liquids are filled then we can say that pressure at same level of same liquid is same.
Q. In a U-tube 20 cm of a liquid of density `rho` is on left hand side and 10 cm of another liquid of density 1.5 `rho` is on right hand side in between them there is a third liquid of density `2rho` what is the value of `h`.02:24View Solution_E01_174_Q01.png)
In a U-tube if different liquids are filled then we can say that pressure at same level of same liquid is same.
Q. If small but equal lengths of liquid -1 and liquid -2 are increased in their corresponding sides then h will03:21View SolutionLiquid is filled in a vessel of square base `(2mxx2m)` upto a height of 2m as shown in figure (i). In figure (ii) the vessel is tilted from horizontal at `30^(@)`.

What is the velocity of efflux in this case. Liquid does not spills out?03:28View SolutionLiquid is filled in a vessel of square base `(2mxx2m)` upto a height of 2m as shown in figure (i). In figure (ii) the vessel is tilted from horizontal at `30^(@)`.

What is time of fall of liquid on the ground?02:56View SolutionLiquid is filled in a vessel of square base `(2mxx2m)` upto a height of 2m as shown in figure (i). In figure (ii) the vessel is tilted from horizontal at `30^(@)`.
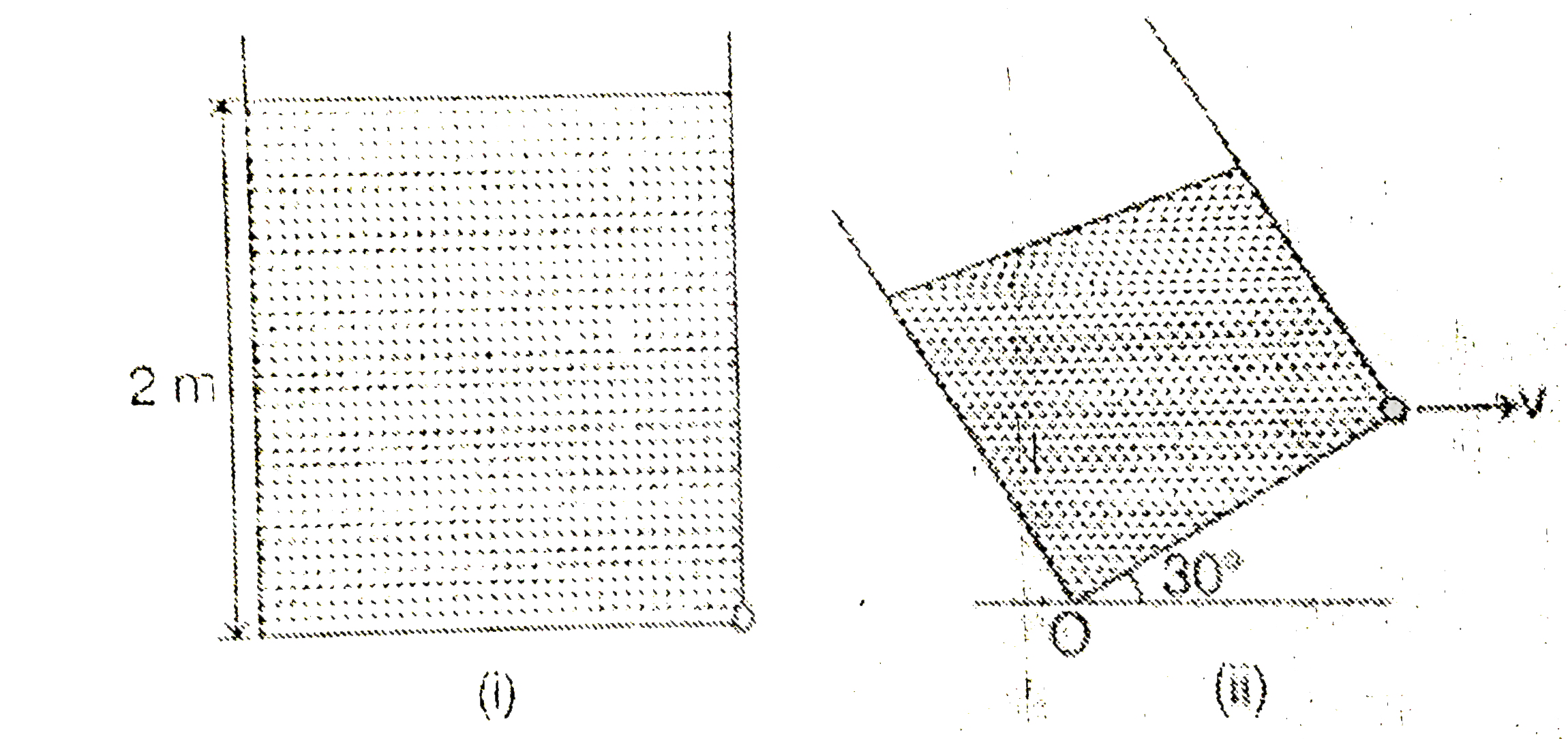
At what distance from point O, will the liquid strike on the ground?03:12View SolutionA cube (side `=10 cm`) of density `0.5 g//cm^(3)` is placed in a vessel of base area `20 cmxx20 cm`. A liquid of density `1.0 g/ cm^(2)` is gradually filled in the vessel at a constant rate `Q=50 cm^(3)//s`

If we plot a graph between the normal reaction on cube by the vessel versus time. The graph will be like02:21View SolutionA cube (side `=10 cm`) of density `0.5 g//cm^(3)` is placed in a vessel of base area `20 cmxx20 cm`. A liquid of density `1.0 g/ cm^(2)` is gradually filled in the vessel at a constant rate `Q=50 cm^(3)//s`
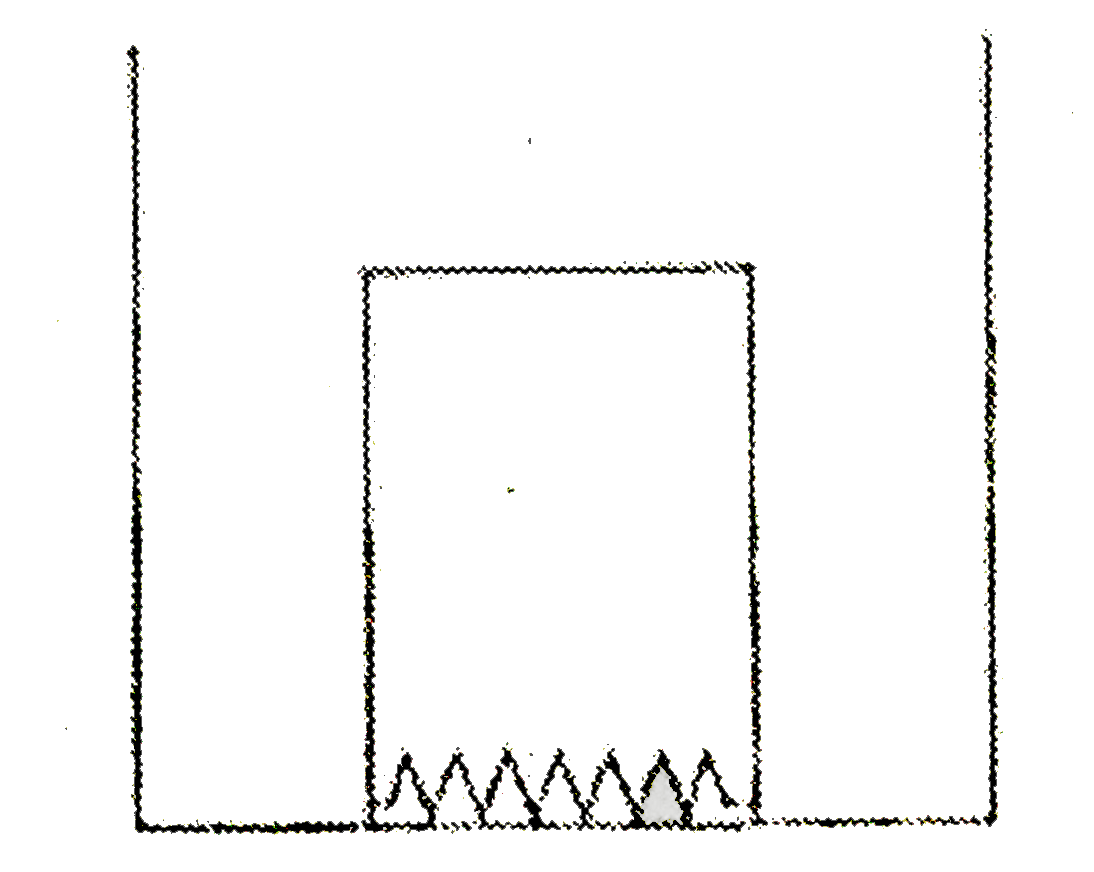
The cube will leave contact with the vessel after time t= ......... s.02:37View Solution_E01_175_Q01.png)
Newton's laws of motion can be applied to a block in liquid also force due to liquid (e.g. upthrust) are also considered in addition to other forces. A small block of weight W is kept inside. The block is attached with a string connected to the bottom of the vessel. Tension in the string is `W//2`
Q. The string is cut. find the time when it reaches the surface of the liquid02:31View Solution_E01_176_Q01.png)
Newton's laws of motion can be applied to a block in liquid also force due to liquid (e.g. upthrust) are also considered in addition to toher forces. A small block of weight W is kept inside. The block is attached with a string connected to the bottom of the vessel. Tension in the string is `W//2`
Q. If weight of the block is doubled then tension in the string becomes x times and the length calculated from above becomes y times then03:10View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density `rho` and height h is filled over another liquid of density `2rho`. Speeds of liquid ejecting from two holes are say `v_(1)` and `v_(2)`.

The ratio `v_(1)/v_(2)` will be02:21View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density `rho` and height h is filled over another liquid of density `2rho`. Speeds of liquid ejecting from two holes are say `v_(1)` and `v_(2)`.

If density of lower liquid is increased02:36View SolutionA cubical vessel (open from top) of side L is filled with a liquid of density `rho`.
What is the torque of hydrostatic force on a side wall about an axis passing through one of the bottom edges?06:50View SolutionA cubical vessel (open from top) of side L is filled with a liquid of density `rho`.
What is the ratio of magnitude of torque on one side wall to the torque on base about the same axis06:50View SolutionA siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figure.

(a) Find the velocity of the liquid through the siphon.
(b) Find the pressure at the highest point B.
(c ) Find the pressure at point C.06:19View SolutionA siphon tube is discharging a liquid of density
`900(kg)/(m^(3))` as shown in figure. `(P_(0)=1.01xx10^(5) N//m^(2))`

Pressure at point B is02:13View SolutionA siphon tube is discharging a liquid of density
`900(kg)/(m^(3))` as shown in figure. `(P_(0)=1.01xx10^(5) N//m^(2))`
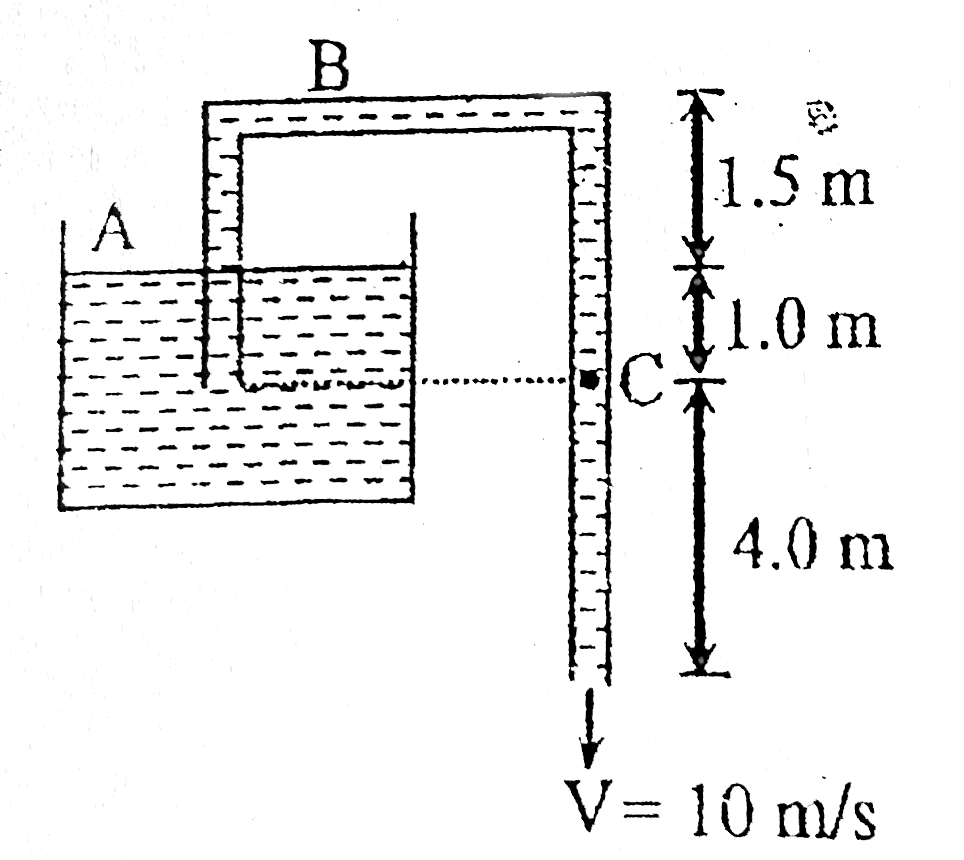
Pressure at point C is02:20View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density `rho`. Given angle of contact `=0^(@)`.
The work done by surface tension will be06:02View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density `rho`. Given angle of contact `=0^(@)`.
What is the potential energy acquired by the liquid in the capillary?02:20View SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density `rho`) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is `P_(0)`. It is observed that the capillary retains some liquid.
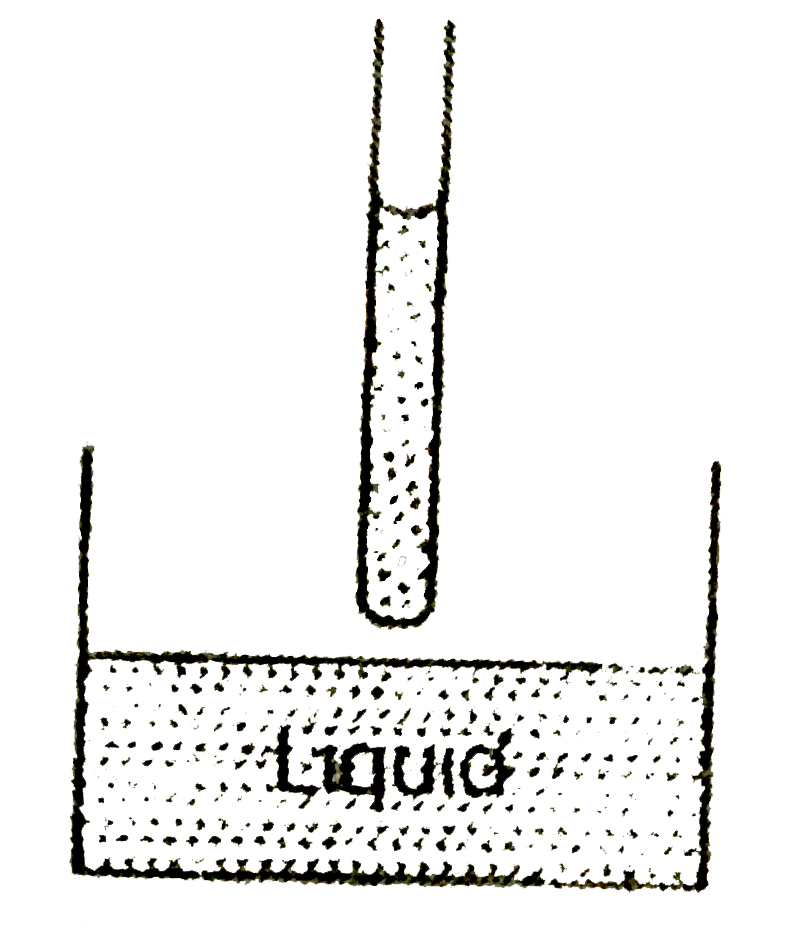
The radius of curvature of meniscus at the bottom of tube is01:52View SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density `rho`) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is `P_(0)`. It is observed that the capillary retains some liquid.
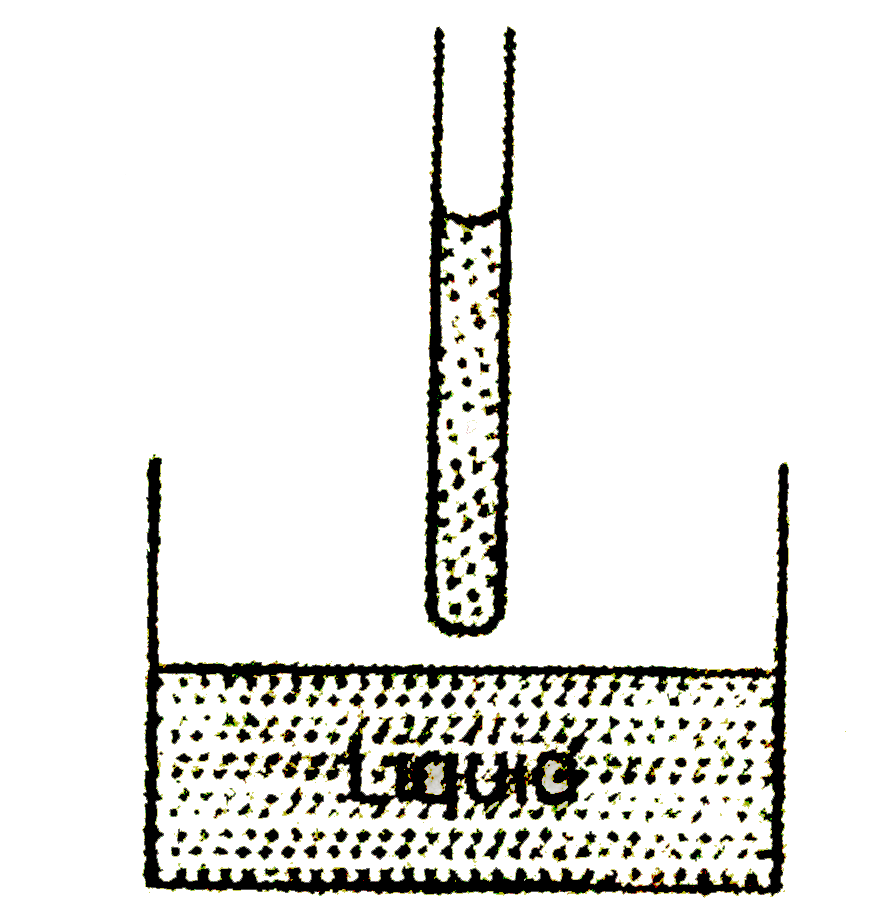
The length of liquid column retained in the capillary is02:31View SolutionIn two identical communicating vessel we poured water (see picture). In one of them we put an ice ball of volume `V=100 cm^(3)` which gets exactly half immersed in the water. The density of water `rho_(w)=1000kg//m^(3)` the density of ice `rho_(i)=900kg//m^(3)`

Select the correct statement (s). Soon after placing the ice ball in left vessel.02:41View SolutionIn two identical communicating vessel we poured water (see picture). In one of them we put an ice ball of volume `V=100 cm^(3)` which gets exactly half immersed in the water. The density of water `rho_(w)=1000kg//m^(3)` the density of ice `rho_(i)=900kg//m^(3)`

After a long time, select the correct statement (s)02:26View SolutionSoap bubble of radius R is blown at one end of a pipe of circular of circular cross-section of radius R as shown in diagram. On the vertical portion of pipe, there is a piston of mass m. T is surface tension of liquid.

Find the mass of piston for which it remain in equilibrium01:35View SolutionSoap bubble of radius R is blown at one end of a pipe of circular of circular cross-section of radius R as shown in diagram. On the vertical portion of pipe, there is a piston of mass m. T is surface tension of liquid.

If piston is slightly displaced in downward direction, then its acceleration when radius of bubble grows to 2R is02:51View SolutionA container contains three liquds as shown in the figure. The specific gravity of liquid 1 and liquid 2 are 0.8 and 1.2 respectively. A small hole having area `10^(-6) m^(2)` at point P is as shown in the figure. Initially hole is closed. The cross-sectional area of container is `50 cm^(2)`. assume all liquids ae ideal and neglect any type of friction between liquid and container. (Given that `g=9.8 m//s^(2)` and `h=28 cm`)
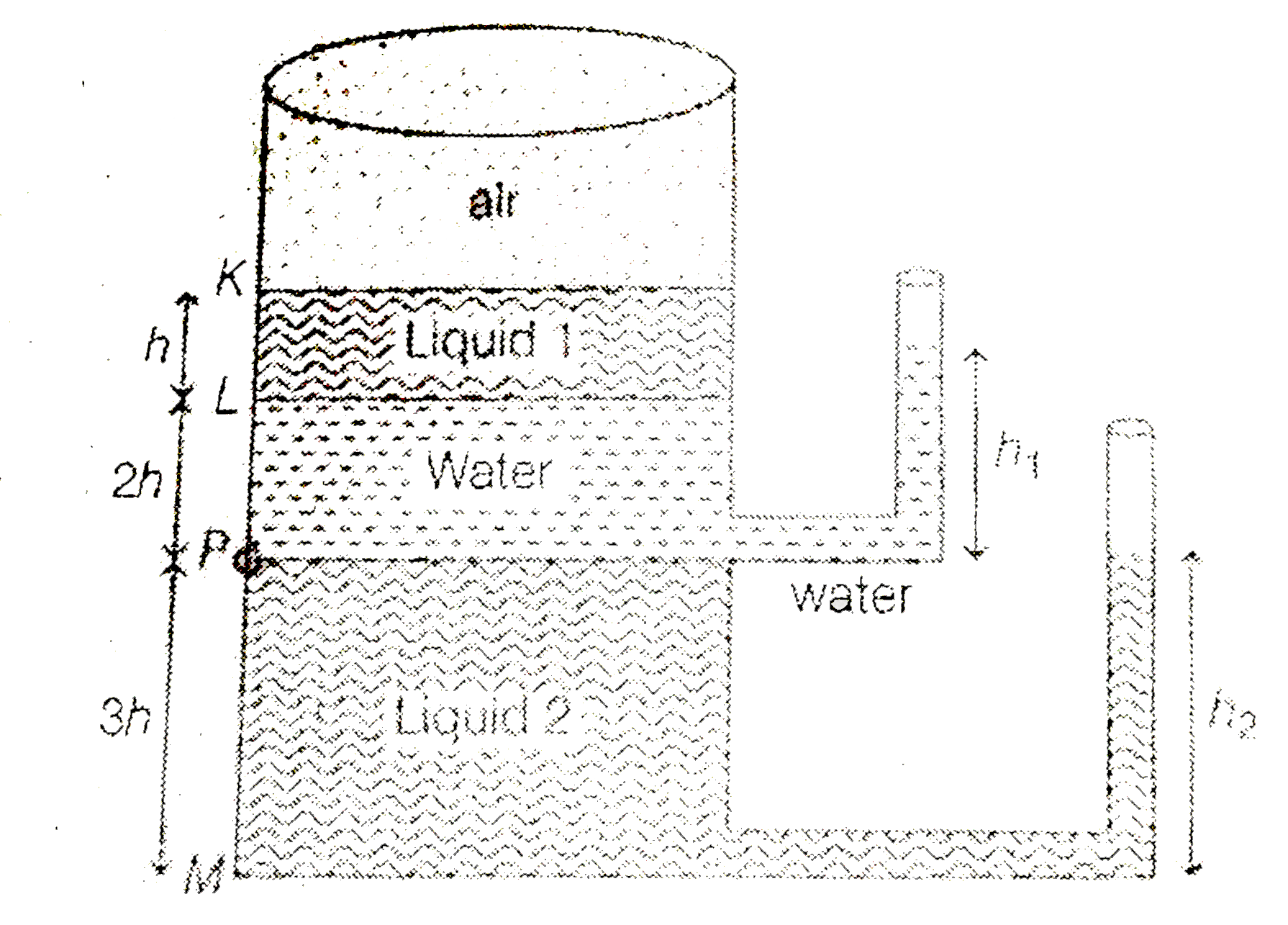
The value of `h_(2)//h_(1)` is03:51View SolutionA container contains three liquds as shown in the figure. The specific gravity of liquid 1 and liquid 2 are 0.8 and 1.2 respectively. A small hole having area `10^(-6) m^(2)` at point P is as shown in the figure. Initially hole is closed. The cross-sectional area of container is `50 cm^(2)`. assume all liquids ae ideal and neglect any type of friction between liquid and container. (Given that `g=9.8 m//s^(2)` and `h=28 cm`)
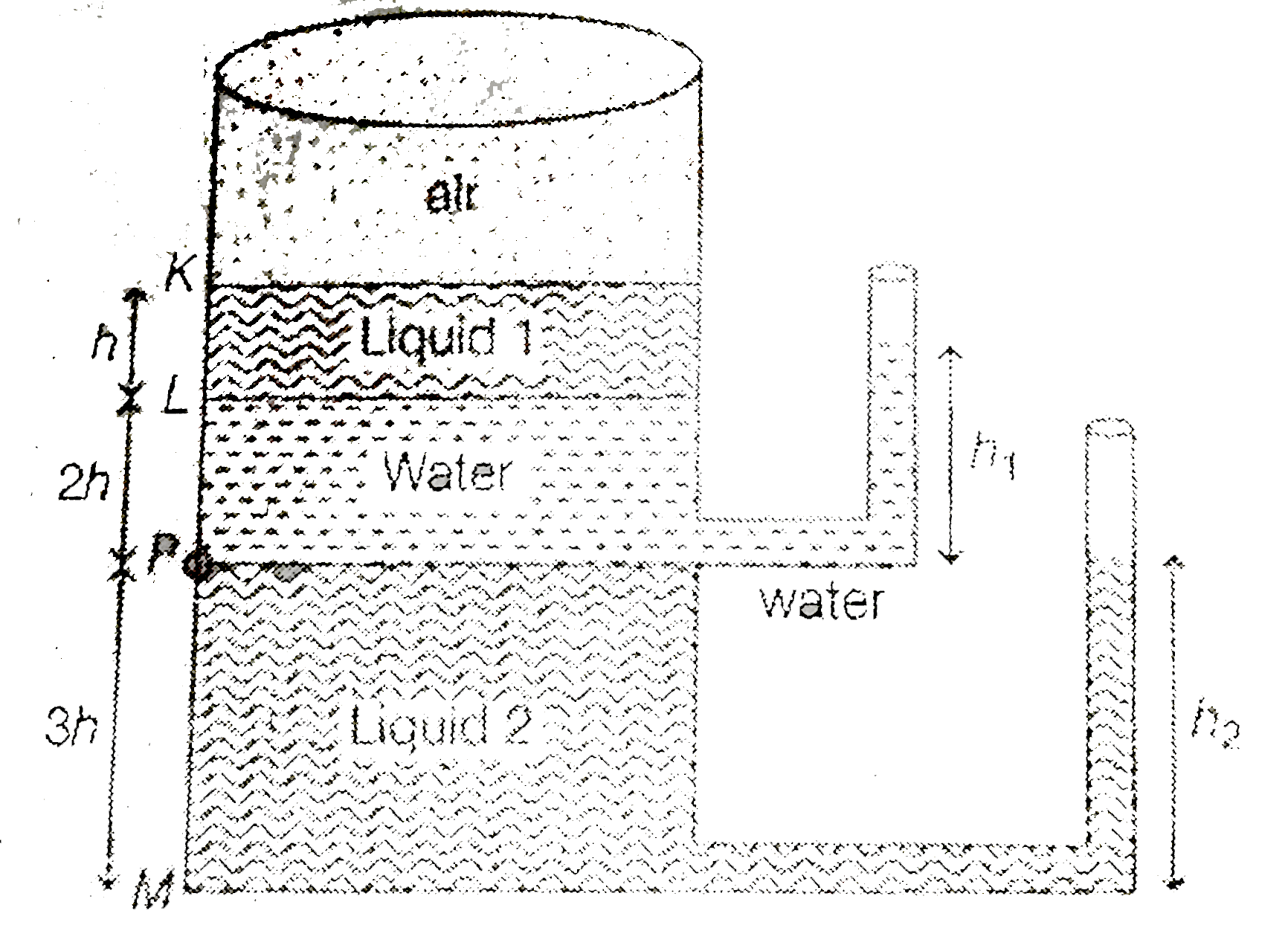
At some instant, hole is opened. the speed of water coming out from hole just after the opening of hole is02:22View SolutionA tank contains water on top of mercury . A cube of iron, 60mm along each edge, is sitting upright in equilibrium in the liquids. Find how much of it is in each liquid. The densities of iron and mercury are `7.7xx10^(3)kg//m^(3)` and `13.6xx10^(3) kg//m^(3)` respectively
 03:12View Solution
03:12View SolutionA tank contains water and mercury as shown in figure. An iron cube of edge `d=6` cm is in equilibrium as shown. (density of iron `=7.8xx10^(3) kg//m^(3)`, density of mercury `=13.6xx10^(3) kg//m^(3)`, density of water `=10^(3) kgm^(3)`)(Neglect the atmospheric pressure)

Time period of small oscillations of block is05:42View SolutionA ring of radius R is made of a thin wire of material of density `rho`, having cross-section area a and Young's modulus y. The ring rotates about an axis perpendicular to its plane and through its centre. Angular frequency of rotation is `omega`.
The tension in the ring will be02:41View SolutionA ring of radius R is made of a thin wire of material of density `rho`, having cross-section area a and Young's modulus y. The ring rotates about an axis perpendicular to its plane and through its centre. Angular frequency of rotation is `omega`.
The ratio of kinetic energy to potential energy is02:57View SolutionA thin uniform copper rod length `l` and mass m rotates unifomly with an angular velocity `omega` about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is `sigma_(max)`, cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions

The maximum angular velocity with which the rod can rotate so that is won't break, is03:27View SolutionA uniform rod of length `l`, mass `m`, cross-sectional area `A` and Young's modulus `Y` is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity `omega`. Find the total extension in the rod due to the tension produced in the rod.
06:45View Solution
Comprehension questions and complete solutions for chapter PROPERTIES OF MATTER of DC PANDEY PHYSICS (HINGLISH) of Class 11
