Complete Solutions to Only One Option is Correct of chapter MAGNETIC EFFECT OF CURRENT AND MAGNETISM of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MAGNETIC EFFECT OF CURRENT AND MAGNETISM |
| DC PANDEY MASTER PROBLEM PACKAGE | Only One Option is Correct |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
Equal currents `i=1` A are flowing through the wires parallel to y-axis located at `x=+1m, x=+2m, x=+4m` and so on...., etc. but in opposite directions as shown in Fig The magnetic field (in tesla) at origin would be
 03:46View Solution
03:46View SolutionSame current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
07:31View SolutionTwo identical particles having the same mass m and charges +q and -q separated by a distance d enter a uniform magnetic field B directed perpendicular to paper inwards with speeds `v_1 and v_2` as shown in Fig. 1.139. The particles will not collide if
 06:22View Solution
06:22View SolutionFind the magnetic field at `P` due to the arrangement shown
 .07:43View Solution
.07:43View SolutionA wire of length 1 m placed in x-z plane carries current of 1 amp. The coefficient of friction between wire and the surface is `0.2` and mass of the wire is 2. The magnetic field of strengh 2 T exists along position y direction . Then choose the correct statment .
02:31View SolutionA charge particle having charge q expericenec a `F_(1)q=(-hatj+hatk)N ` in a magnetic field B when is has velocity `v_(1)=(1.0)hati(m)/(s)`. The force becomes `F=q(hati-hatl)` when the velocity is charged to `F=q(hati-hatl)` magnetic induction vector at that point is
View SolutionA change particule is projected with velocity `v_(0)` at positive x-axis .The magnetic field B is direction s negative z-aixs between `x=0` and `x=l` . The particule emerges out (at x =L) at an angle of `60^(@)` with direction of projected (at x = 0) a positive x-axis so that wahen it emerges out (at x = L) the angle made by it is `30^(@)` with the direction projection
02:59View SolutionThe dimensions of `(B^(2)R^(2)C^(2))/(2mu_(0))` (Where B is magnetic filed, and `mu_(0)` is permeability of free space , R resistance and C is capacitance) is
02:35View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination `theta` with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field `vec B` exists in space. Then, magnitude of magnetic field `vec B` is
 02:21View Solution
02:21View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field `vec E = E_0 hat i and vec B = B_0 hat i` with a velocity `vec v = v_0 hat j`. The speed of the particle will become `2v_0` after a time.
08:40View SolutionA rigid circular loop of radius `r` and mass `m` lies in the `XY-` plane of a flat table and has a current `I` flowing in it. At this particular place. The Earth's magnetic field `vec(B)=B_(x)i+B_(z)k`. The value of `I` so that the loop starts tilting is `:`
03:57View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
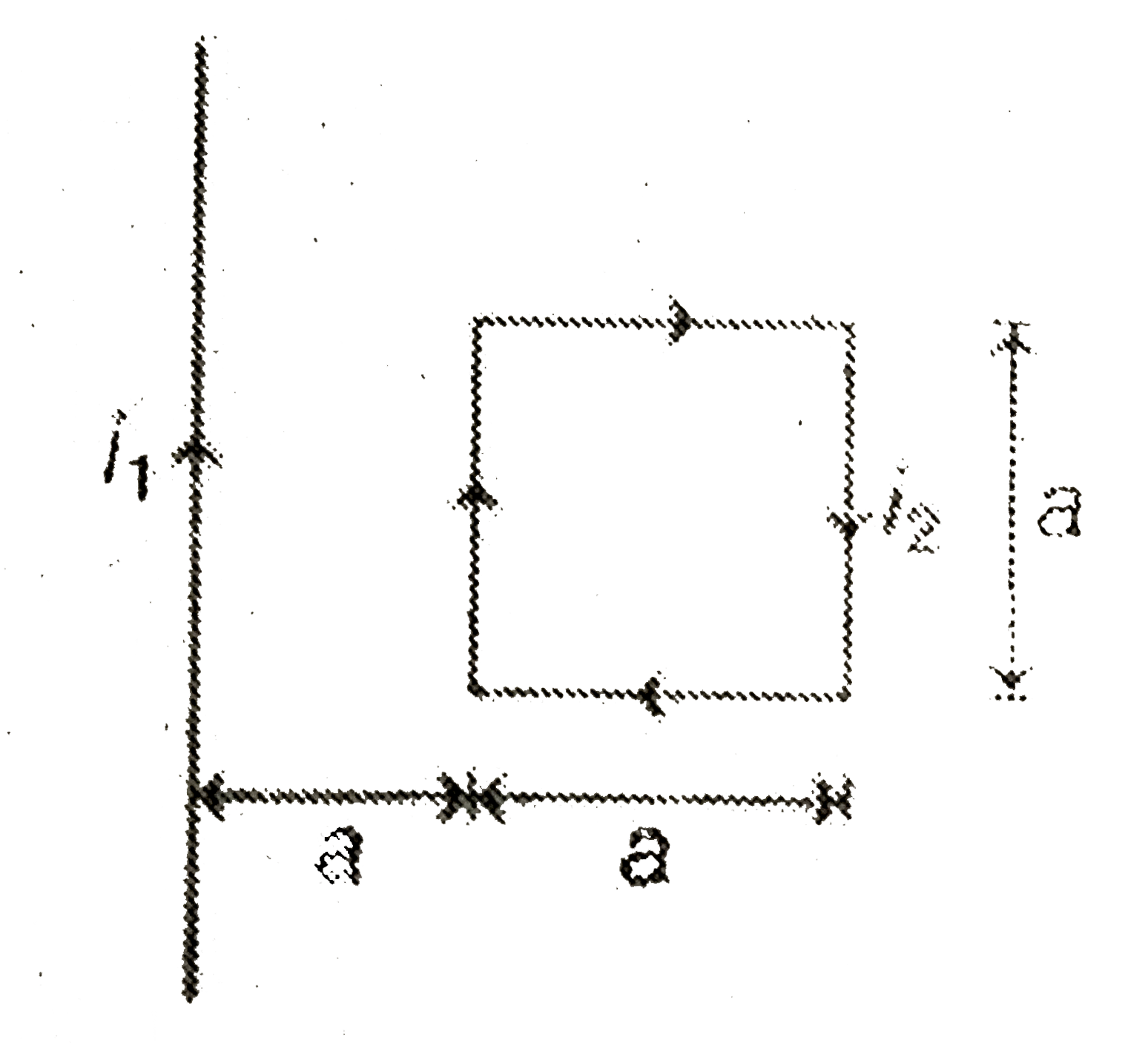 01:51View Solution
01:51View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
02:45View SolutionA particle of charge per unit mass `alpha` is released from origin with a velocity `vecv=v_(0)hati` in a magnetic field
`vec(B)=-B_(0)hatk` for `xle(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
and `vec(B)=0` for `xgt(sqrt(3))/2 (v_(0))/(B_(0)alpha)`
The `x`-coordinate of the particle at time `t((pi)/(3B_(0)alpha))` would be03:27View SolutionThe x -co- ordinates of the particle at time t `(gt(pi)/(3B_(0)alpha))` would be
View SolutionTwo wires AO and OC carry equal currents i as shown in Fig. One end of both the wires extends to infinity. Angle AOC is `alpha`. The magnitude of magnetic field is point P on the bisector of these two wires at a distance r from point O is
 03:33View Solution
03:33View SolutionFigure shows a square current carrying loop `ABCD` of side `2m` and current` i=(1)/(2)A`. The magnetic moment `vec(M)` of the loop is
 07:55View Solution
07:55View SolutionA conducting ring of mass 2kg and radius `0.5m` is placed on a smooth plane. The ring carries a current of `i=4A`. A horizontal magnetic field `B=10 T` is switched on at time `t=0` as shown in fig The initial angular acceleration of the ring will be
 .03:27View Solution
.03:27View SolutionA charge praticule of sepeific charge (charge/ mass ) `alpha` is realsed from origin at time t=0 with velocity `v= v_(0)(hati+hatj)` in unifrom magnetic fields `B= B_(0)hati`. Co-ordinaties of the particle at time `t = (pi)/(B_(0)alpha)` are
04:28View SolutionMagnetic moment of an electron in nth orbit of hydrogen atom is
03:52View SolutionTwo very long straight parallel wires carry steady currents `i` and `2i` in opposite directions. The distance between the wires is `d`. At a certain instant of time a point charge `q` is at a point equidistant from the two wires in the plane of the wires. Its instantaneous velocity `vecv` is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on t he charge at this instant is
02:33View SolutionIn Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
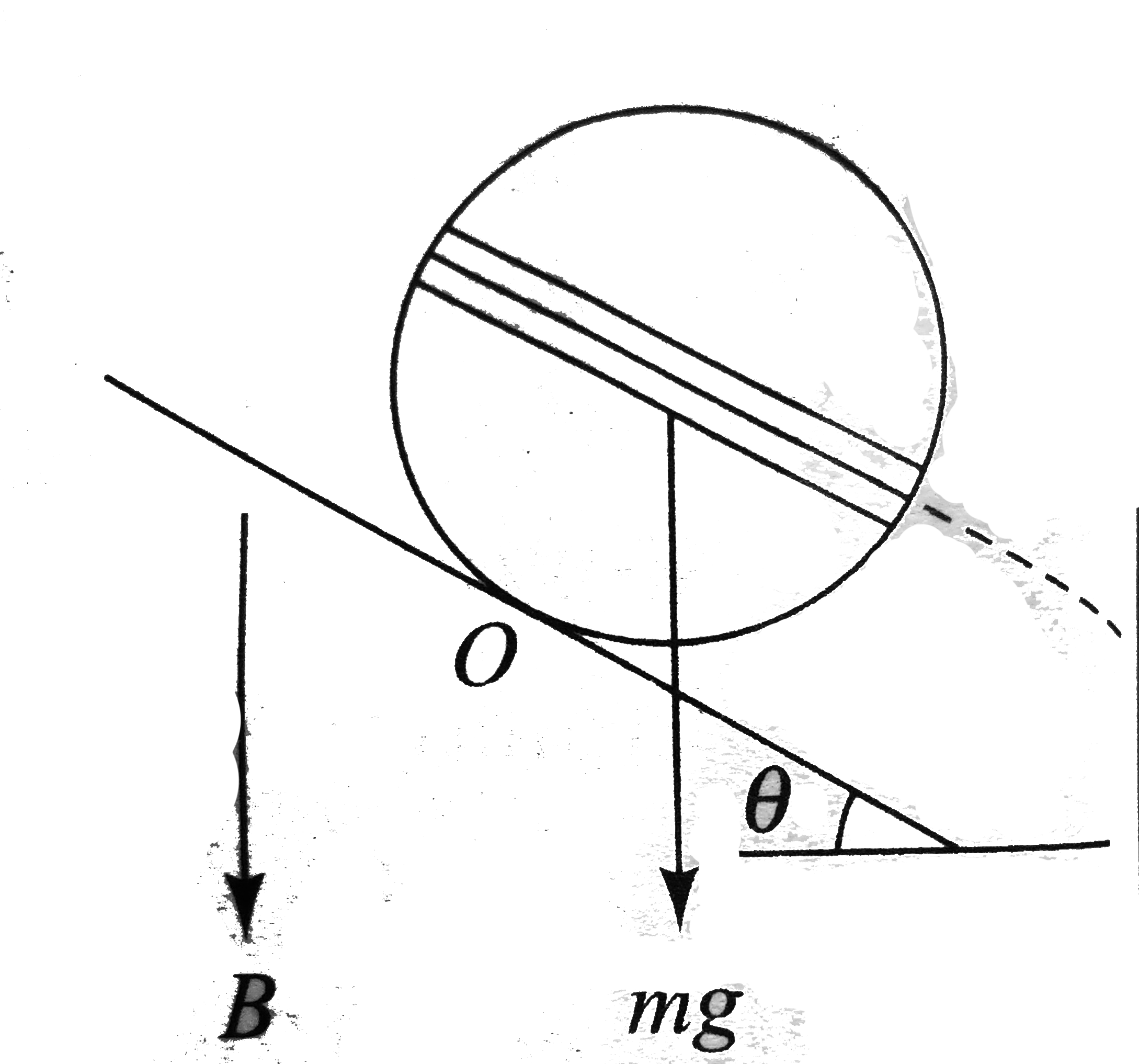 03:30View Solution
03:30View SolutionA particule having charge q enters a rection of untiormal magnetic field B (direction inwards) and in denfectro as shown . The magnetic of the momentum of the particles is
 02:27View Solution
02:27View SolutionA particle of specific charge (charge/mass) `alpha` starts moving from the origin under the action of an electric field `oversetrarrE = E_(0)hati` and magnetic field
`oversetrarrB = B_(0)hatk` Its velocity at `(x_(0),y_(0).0)` is `(4hati +3hatj)` The value of `x_(0)` is .03:42View SolutionA conducting wire bent in the from of a parabola `y^(2)=2x` carries a current `i=2A` as shown in figure This wire is placed in a unifrom magnetic field
`oversetrarrB = - 4hatk` Tesla The magnetic force on the wire is (newton)
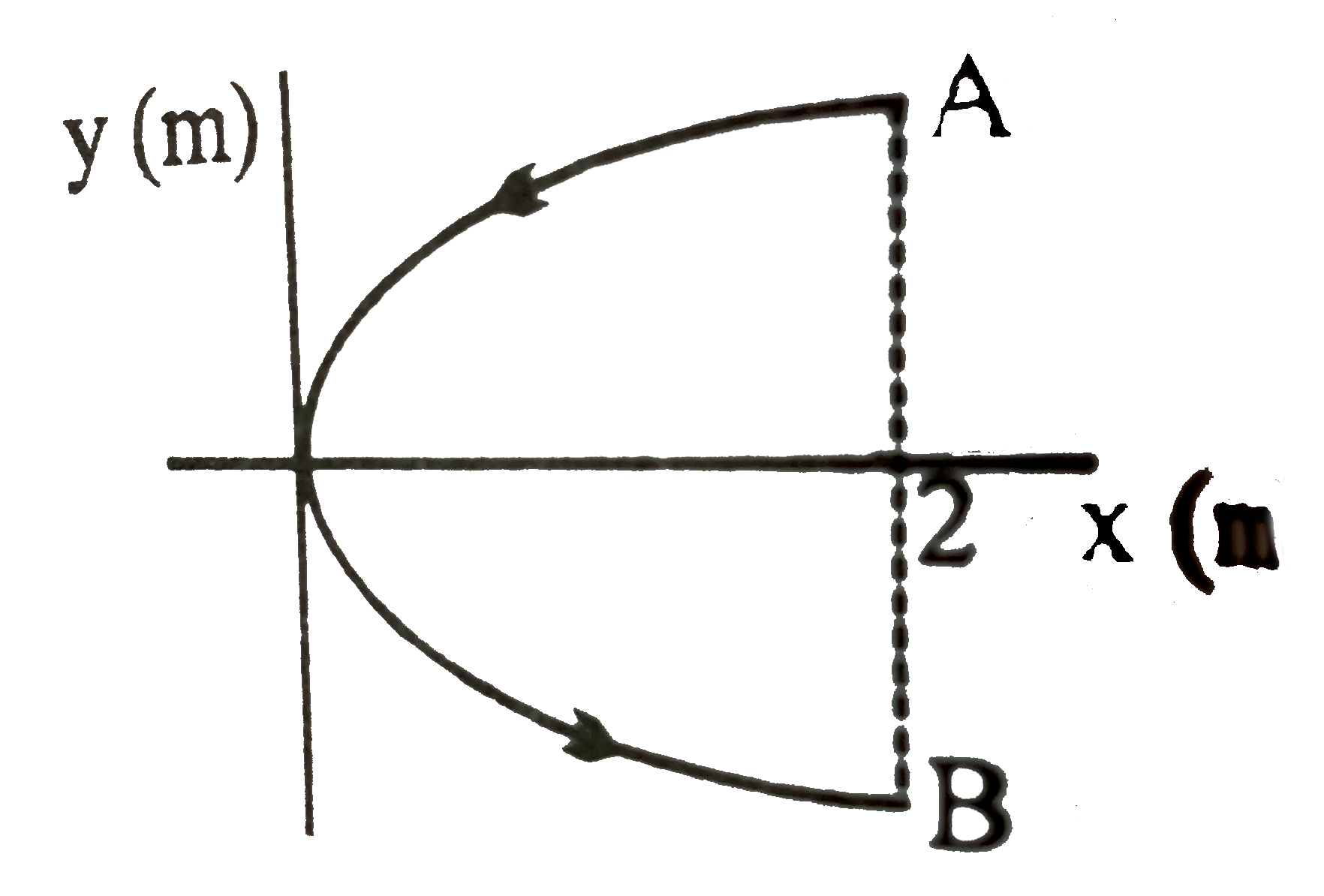 .02:23View Solution
.02:23View SolutionA rectangular loop PQRS made from a uniform wire has length a, width b and mass m. It is free to rotate about the arm PQ, which remains hinged along a horizontal line taken as the y-axis (see figure). Take the vertically upward direction as the z-axis. A uniform magnetic field `vec(B) = (3 hat(i) + 4 hat(k)) B_(0)` exists in the region. The loop is held in the x-y plane and a current I is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium

(a) What is the direction of the current I in PQ?
(b) Find the magnetic force on the arm RS.
(c) Find the expression for I in terms of `B_(0)`, a, b and m13:46View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
00:57View SolutionA rectangular loop carrying a current ` i` is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current ` I` is established in the wire as shown in the figure ,
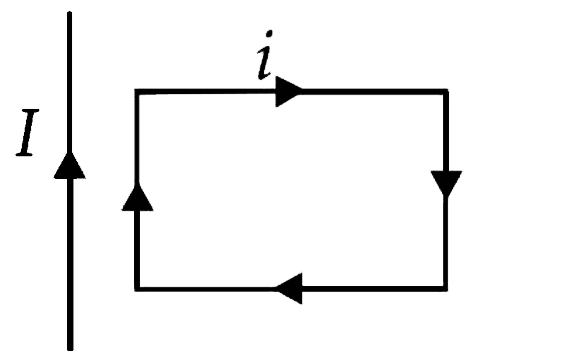 02:40View Solution
02:40View SolutionKinetic energy of a charged particle is zero at time `t_(0)`. K at time 2 `t_(0)`. 2K at time 3 `t_(0)`. It remains constant (i.e.2K) upto 4 `t_(0)`. Choose the correct option.
01:59View SolutionThree infinetely long wires 1 , 2 and 3 carry equal currents in the directions shown in fiugre. They are placed on the vertices of an equilateral triangle. Let F be the magnitude of force between any two wires.

`F_(1)` is the magnitude of force on wire 1 and `F_(2)` the magnitude of force on wire 2. Then03:01View SolutionA change q=1 C is at (3m,4m) and moving towards positive x-axis with constant velocity of 4 `m//s`. A long current carrying wire is at origin. Current in this wire is 2.A and towards positive z-axis. Magnetic force on the charge at given instant is
02:57View SolutionTwo identical magnetic dipoles of magnetic moments `1*0Am^2` each are placed at a separation of `2m` with their axes perpendicular to each other. What is the resultant magnetic field at a point midway between the dipoles?
04:02View SolutionA cylinder wire of radius R is carrying uniformly distributed current I over its cross-section. If a circular loop of radius r is taken as amperian loop, then the variation value of `oint vec(B)* Vec(dl)` over this loop with radius 'r' of loop will be best represented by
05:19View SolutionA uniform magnetic field `vec(B) = 3 hat i + 4 hat j + hat k` exists in region of space. A semicircular wire of radius of 1 m carrying current 1 A having its centre at (2, 2, 0) is placed in x-y plane as shown in Fig. The force on semicircular wire will be
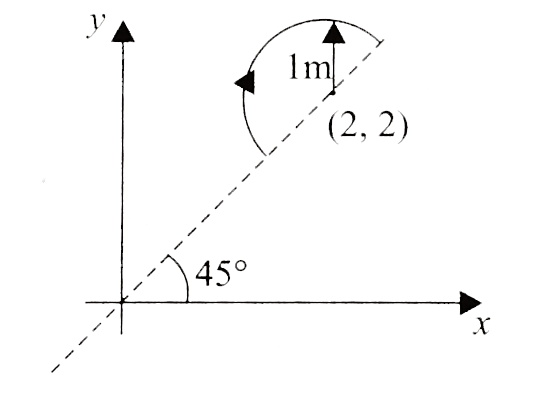 04:15View Solution
04:15View SolutionIn the figure shown a current `I_(1)` is established in the long straight wire AB. Another wire CD carrying currrent `I_(2)` is placed in the plane of the paper. The line joining the ends of this wire is perpendicular to the wire AB. The resultant force on the wire CD is :
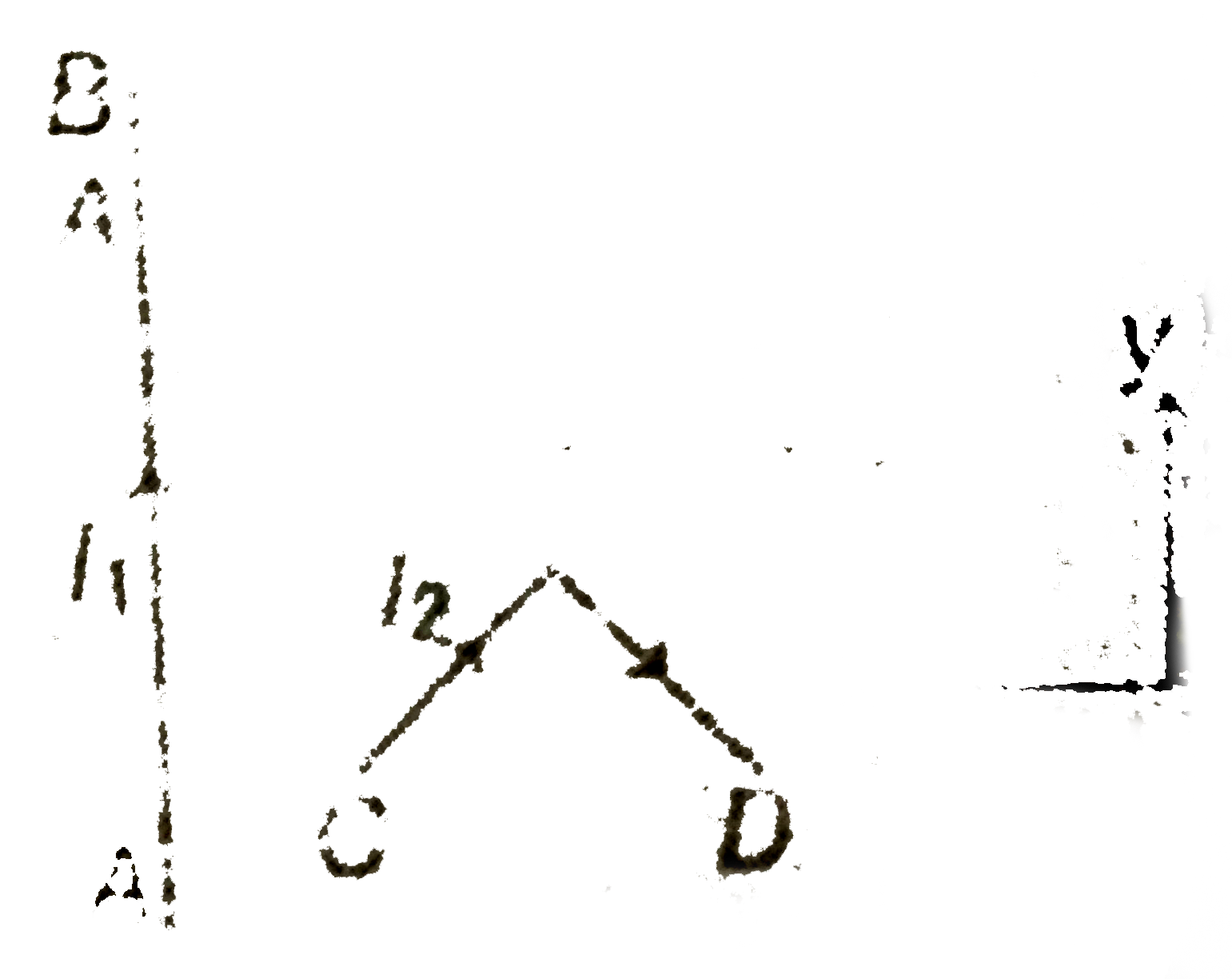 01:58View Solution
01:58View SolutionAn `alpha` is moving along a circle of radius R with a constant angular velocity `omega`. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by the `alpha`-particle. If the minimum time interval between two successive time at which A records zero magnetic field is t, the angular speed `omega`, in terms of t, is
03:06View SolutionA long straight metal rod has a very long hole of radius `'a'` drilled parallel to the rod axis as shown in the figure. If the rod carries a current `I`, find the magnetic field on axis of hole. Given `C` is the centre of the hole and `OC=c`.
 04:00View Solution
04:00View SolutionA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
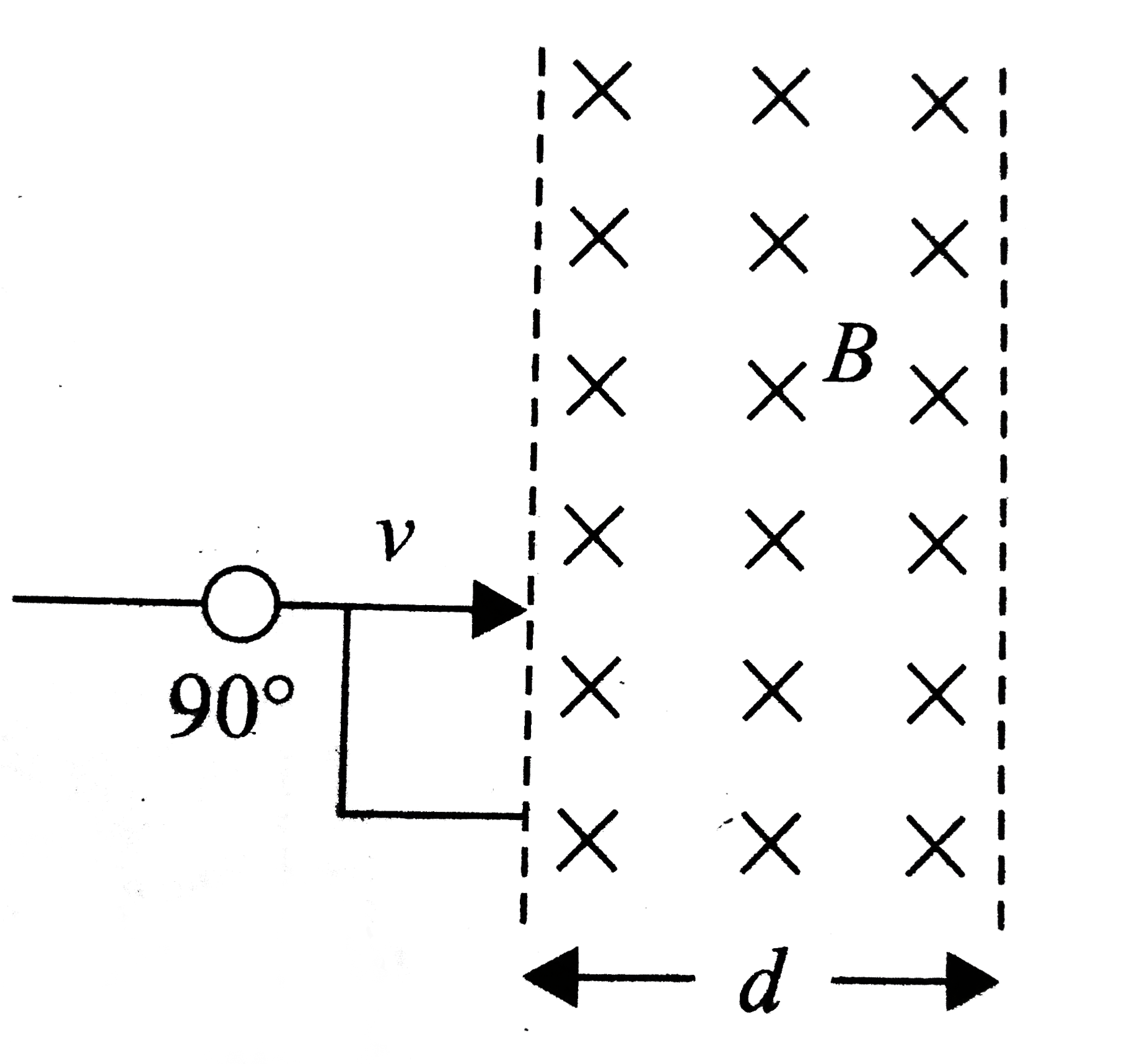 04:26View Solution
04:26View SolutionRefer to the figure. Rectangle PQRS represents the cross section of a uniform magnetic field region of 0.20 T. An electron is projected at a speed of `V=2.0xx10^(6)m//s` into the region at an angle of `30^(@)` to the direction of the mangetic field. The length of the magnetic field region is 0.01 m. Find the number of revolutions made by the electron before it leaves the magnetic field region.
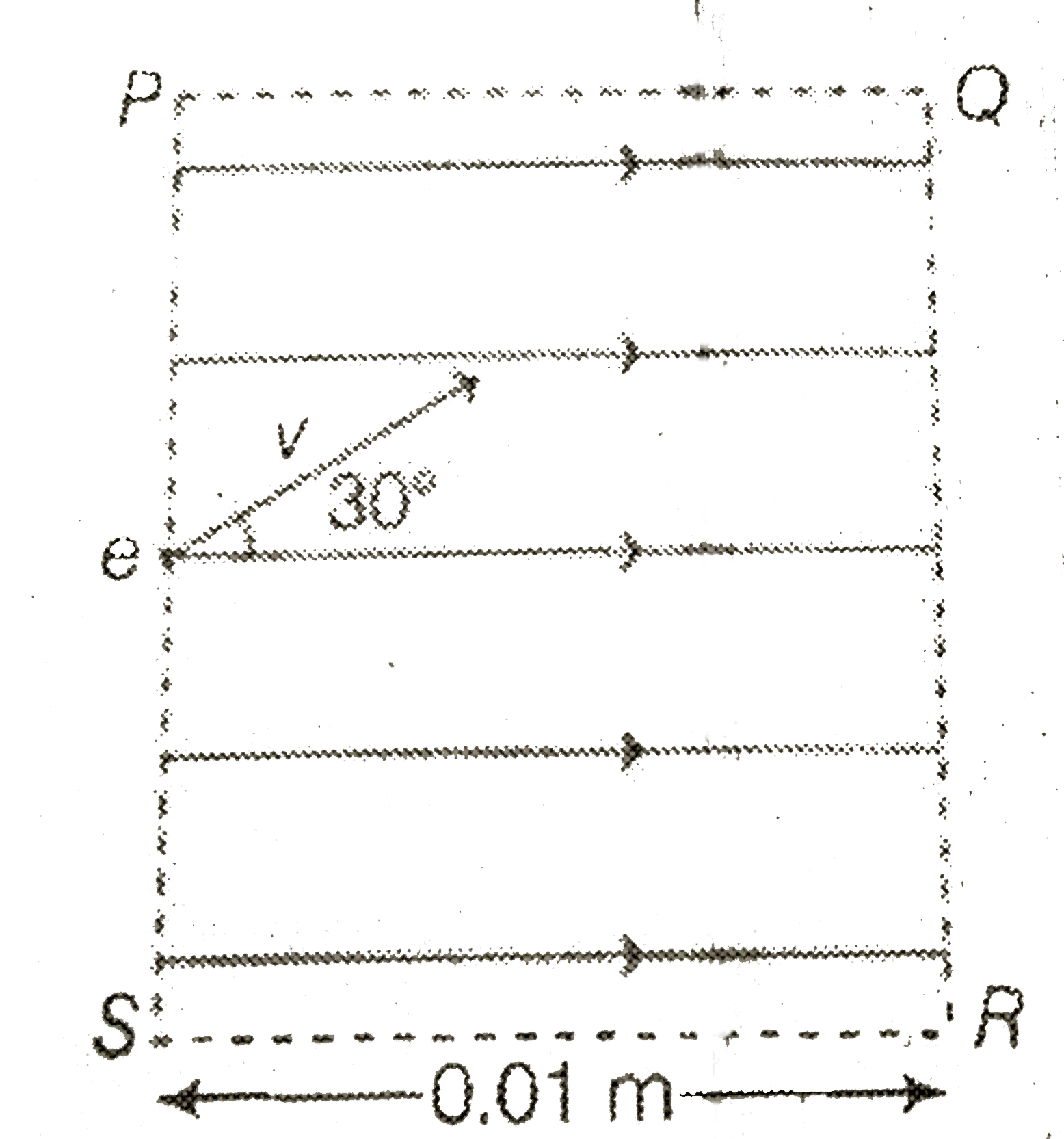 02:21View Solution
02:21View SolutionIn a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed `V=4xx10^(4)m//s` at an angle of `alpha` with the field direction. The proton reaches a point B in the field where its velocity makes an angle `beta` with the field direction. If `(sinalpha)/(sinbeta)=sqrt3.` Find the electric potential difference between the points A and B. Take mp (mass of proton) `=1.6xx10^(-27)`kg and e (magnitude of electronic charge) `=1.6xx10^(-19)`C.
View SolutionA particle of specific charge `q//m = (pi) C//kg` is projected from the origin towards positive x-axis with a velocity of `10 m//s` in a uniform magnetic field `vec(B) = -2 hat K` Tesla. The velocity `vec V` of the particle after time `t =1//6` s will be
04:54View SolutionIn a certain region of space there exists a constant and uniform magnetic field of induction B. The width of the magnetic field is a. A charged particle having charge q is projected perpendicular to B and along the width the field. If deflection produced by the fiel perpendicular to the width is d, then the magnitud of the momentum of the particle is,
 03:18View Solution
03:18View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point 2a, `b//2`, 0 its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
04:22View SolutionThree long wires are placed in xy plane in a gravity free space. 'I' is the current flowing in each wire. The currents are constant in magnitude. Distance between each wire is 'd' and `lamda` is the mass per unit length of each wire. Wires 'A' and wire 'C' are fixed and wire 'B' is slightly displaced along 'z' axis. The period of oscillation of wire 'B' is
 07:19View Solution
07:19View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of `60^(@)` with the boundary surface of magnetic field and comes out at an angle of `30^(@)` with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.
 View Solution
View Solution
Only One Option is Correct questions and complete solutions for chapter MAGNETIC EFFECT OF CURRENT AND MAGNETISM of DC PANDEY PHYSICS (HINGLISH) of Class 11
