Complete Solutions to Level 2 Single Correct of chapter LAWS OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | LAWS OF THERMODYNAMICS |
| DC PANDEY | Level 2 Single Correct |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
The equation of a state of a gas is given by `p(V-b)=nRT`. If 1 mole of a gas is isothermally expanded from volume V and 2V, the work done during the process is
View SolutionThe cyclic process for 1 mole of an ideal gas is shown in the V-T diagram. The work done in AB, BC and CA respectively is

View SolutionTen moles of a diatomic perfect gas are allowed to expand at constant pressure. The initial volume and temperature are `V_0` and `T_0` respectively. If `7/2RT_0` heat is transferred to the gas, then the final volume and temperature are
View SolutionAn ideal monoatomic gas is carried around the cycle ABCDA as shown in the figure. The efficiency of the gas cycle is

View SolutionIn the process shown in figure, the internal energy of and ideal gas decreases by `(3p_0V_0)/(2)` in going from point C to A. Heat transfer along the process CA is
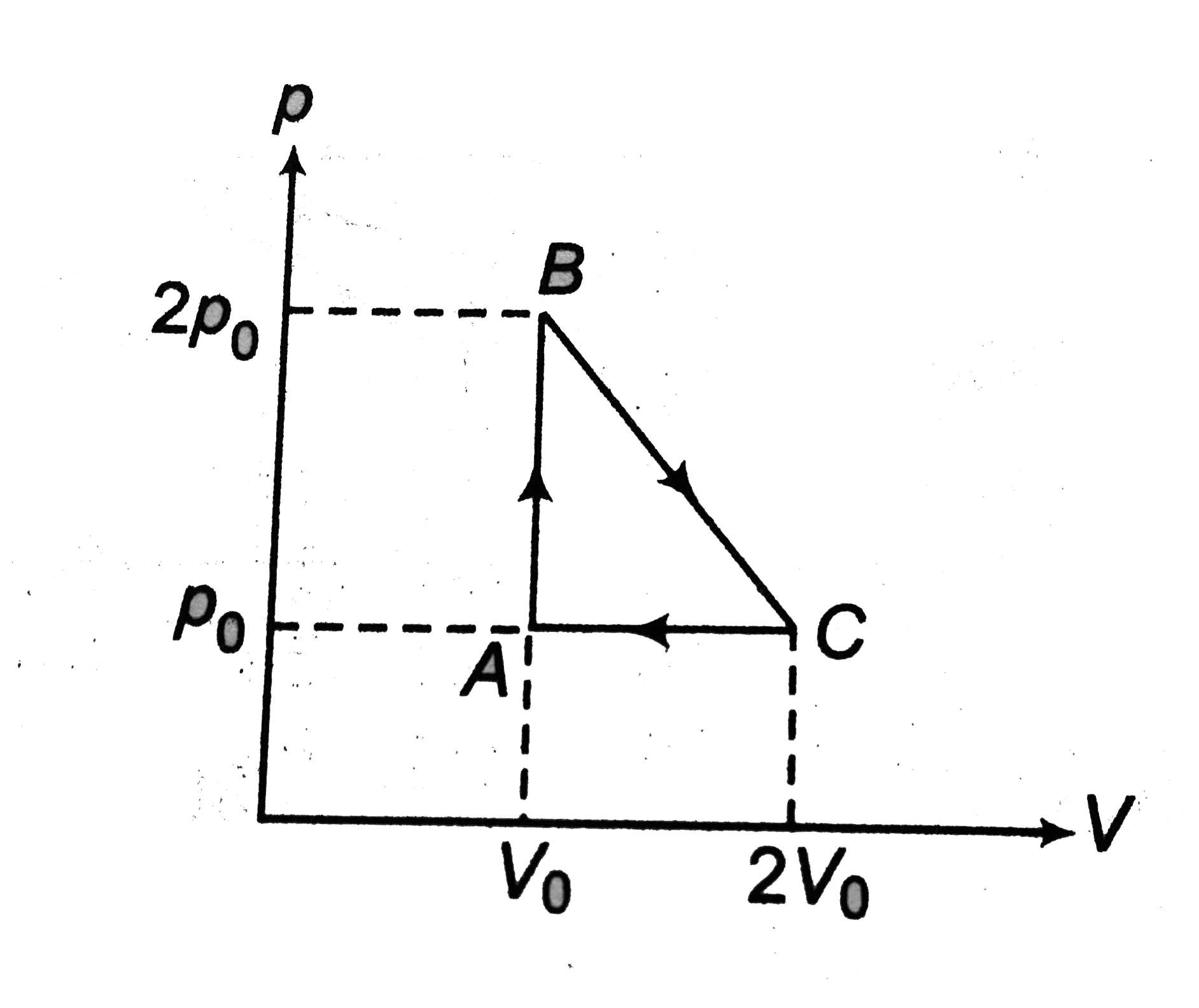
View SolutionOne mole of an ideal monoatomic gas at temperature `T_0` expands slowly according to the law `p/V` = constant. If the final temperature is `2T_0`, heat supplied to the gas is
View SolutionA mass of gas is first expanded isothermally and then compressed adiabatically to its original volume. What further simplest operation must be performed on the gas to restore it to its original state?
View SolutionA monoatomic ideal gas, initially at temperature `T_1,` is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature `T_2` by releasing the piston suddenly. If `L_1 and L_2` are the length of the gas column before expansion respectively, then `(T_1)/(T_2)` is given by
View SolutionOne mole of an ideal gas is taken through a cyclic process. The minimum temperature during the cycle is 300K. Then, net exchange of heat for complete cycle is
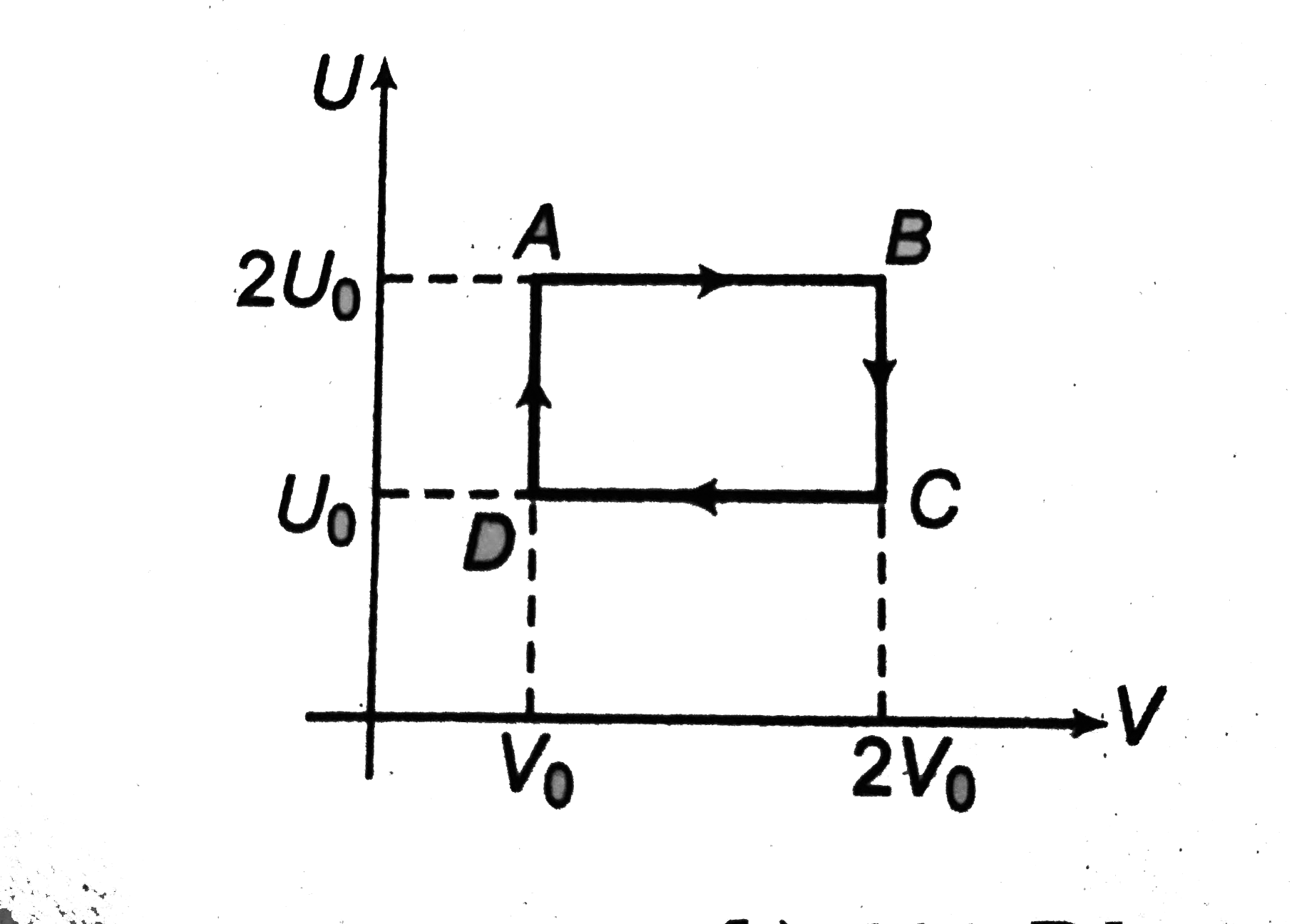
View SolutionTwo moles of an ideal gas are undergone a cyclic process 1-2-3-1. If net heat exchange in the process is 300J, the work done by the gas in the process 2-3 is

View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionA gas follows a process `TV^(n-1)=const ant`, where `T=` absolute temperature of the gas and `V=` volume of the gas. The bulk modulus of the gas in the process is given by
View SolutionOne mole of an ideal gas at temperature `T_` expands slowly according to the law `p/V=` constant.
Its final temperature is `T_2`. The work done by the gas is
View Solution600J of heat is added to a monoatomic gas in a process in which the gas performs a work of 150J. The molar heat capacity for the process is
View SolutionThe internal energy of a gas is given by `U=2pV`. It expands from `V_0` to `2V_0` against a constant pressure `p_0`. The heat absorbed by the gas in the process is
View SolutionThe figure shows two paths for the change of state of a gas from A to B. The ratio of molar heat capacities in path 1 and path 2 is

View Solutionp-T diagram of one mole of an ideal monatomic gas is shown. Processes AB and CD are adiabatic. Work done in the complete cycle is

View SolutionAn ideal monoatomic gas undergoes a process in which its internal energy U and density `rho` vary as `Urho`= constant. The ratio of change in internal energy and the work done by the gas is
View SolutionThe given figure shows the variation of force applied by ideal gas on a piston which undergoes a process during which piston position changes from 0.1 to 0.4m. If the internal energy of the system at the end of the process is 2.5 J higher, then the heat ( in joule ) absorbed during the process is

View SolutionA gas can expand through two processes : (i) isobaric, (ii) `p/V` =constant. Assuming that the initial volume is same in both processes and the final volume which is two times the initial volume is also same in both processes, which of the following is true?
View SolutionAn ideal gas of adiabatic exponent `gamma` is expanded so that the amount of heat transferred to the gas is equal to the decrease of its internal energy. Then, the equation of the process in terms of the variables T and V is
View SolutionA thermodynamical process is shown in the figure with `p_A=3xxp_(atm)`, `V_A=2xx10^-4m^3`, `p_B=8xxp_(atm)`, `V_C=5xx10^-4m^3`. In the process AB and BC, 600J and 200J heat are added to the system. Find the change in internal energy of the system in the process CA. `[1 p_(atm)=10^5N//m^2]`
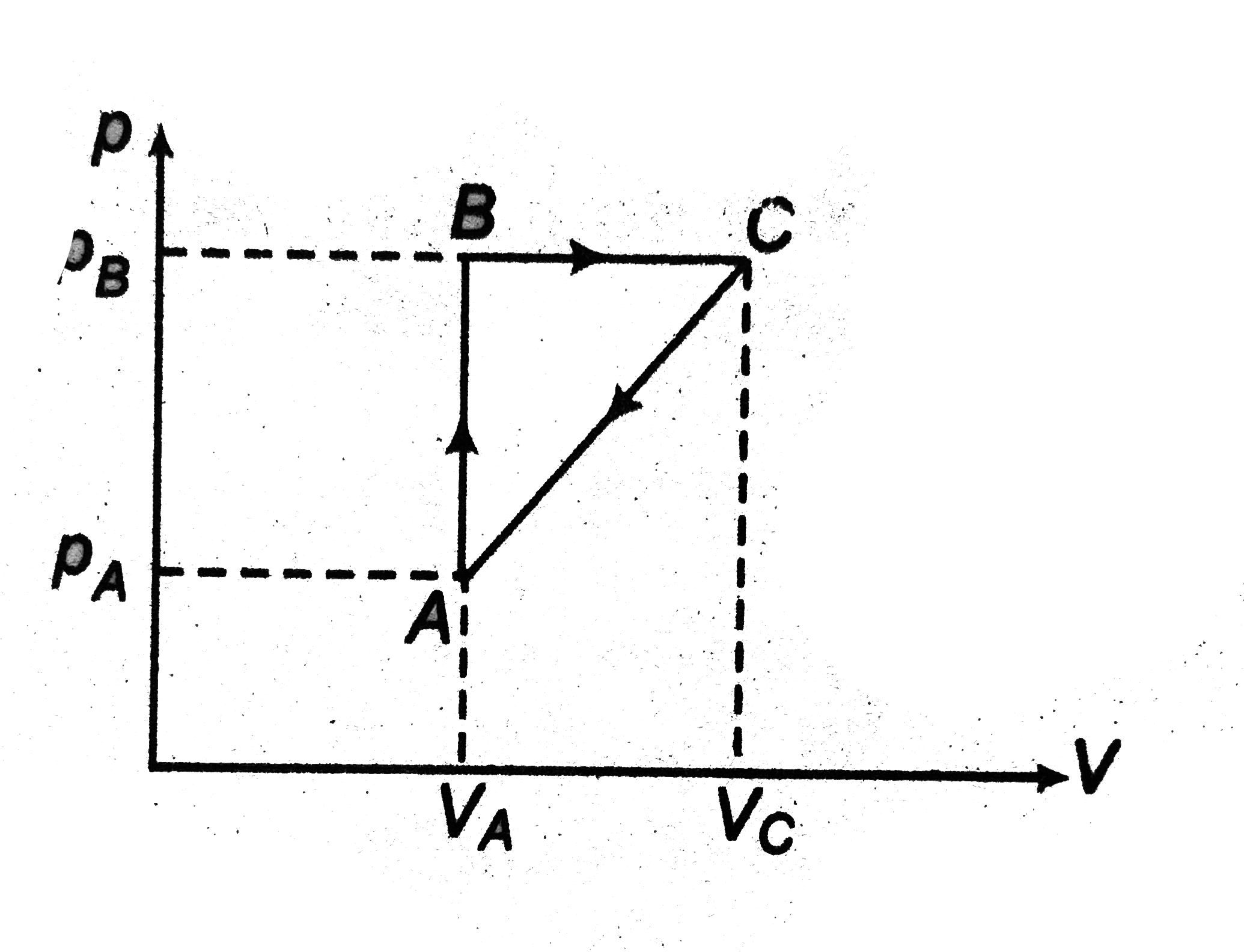
View SolutionA gas takes part in two processes in which it is heated from the same initial state 1 to the same final temperature. The processes are shown on the p-V diagram by the straight lines 1-3 and 1-2. 2 and 3 are the points on the same isothermal curve. `Q_1` and `Q_2` are the heat transfer along the two processes. Then,

View SolutionA closed system receives 200kJ of heat at constant volume. It then rejects 100kJ of heat while it has 50kJ of work done on it at constant pressure. If an adiabatic process can be found which will restore the system to its initial state, the work done by the system during this process is
View Solution100 moles of an ideal monatomic gas undergoes the thermodynamic process as shown in the figure

`ArarrB:` isothermal expansion `BrarrC:` adiabatic expansion
`CrarrD:` isobaric compression `DrarrA:` isochoric process The heat transfer along the process AB is `9xx10^4J`. The net work done by the gas during the cycle is [Take `R=8JK^-1mol^-1`]
View SolutionTwo moles of an ideal monoatomic gas are expanded according to the equation pT=constant form its initial state `(p_0, V_0)` to the final state due to which its pressure becomes half of the initial pressure. The change in internal energy is

View SolutionThe state of an ideal gas is changed through an isothermal process at temperature `T_0` as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is `(p_0)/(2)`, then the pressure of the gas in state C is
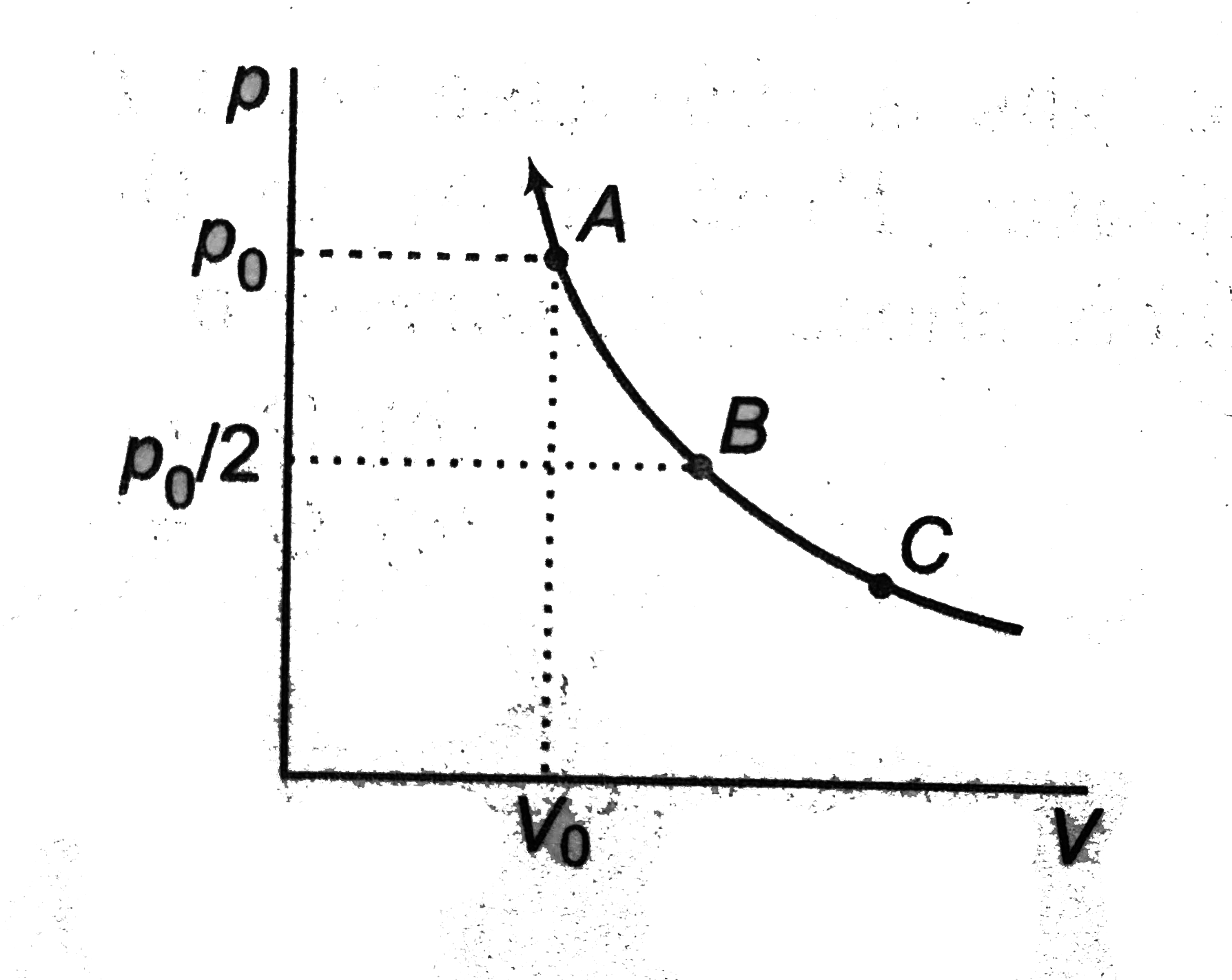
View Solution
Level 2 Single Correct questions and complete solutions for chapter LAWS OF THERMODYNAMICS of DC PANDEY PHYSICS (HINGLISH) of Class 11
All Exercises from DC PANDEY Class 11 PHYSICS LAWS OF THERMODYNAMICS
- Example
- Example Type 1
- Example Type 2
- Example Type 3
- Exercise 21.1
- Exercise 21.2
- Exercise 21.3
- Exercise 21.4
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Objective Questions
- Level 1 Subjective
- Level 2 More Than One Correct
- Level 2 Passage I
- Level 2 Passage II
- Level 2 Single Correct
- Level 2 Subjective
- Miscellaneous Example