Complete Solutions to Multiple CHOICE QUESTIONS [Based on Numerical Problems] of chapter PHYSICAL AND CHEMICAL EQUILIBRIA of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | PHYSICAL AND CHEMICAL EQUILIBRIA |
| DINESH OBJECTIVE CHEMISTRY | Multiple CHOICE QUESTIONS [Based on Numerical Problems] |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
The decomposition of `N_(2)O_(4)` to `NO_(2)` is carried out at `280^(@)C` in chloroform. When equilibrium is reached, `0.2` mol of `N_(2)O_(4)` and `2xx10^(-3)` mol of `NO_(2)` are present in a `2L` solution. The equilibrium constant for the reaction
`N_(2)O_(4) hArr 2NO_(2)` is
View SolutionThe value of the equilibrium constant for the reaction, `2NO +O_(2)hArr 2NO_(2)` is 0.25, then the value of equilibrium constant for `2NO_(2) hArr 2NO+O_(2)` is
View SolutionFor the reaction `N_(2)O_(4)(g) hArr 2NO_(2)(g)` the degree of dissociation at equilibrium is `0.2` at `1` atmospheric pressure. The equilibrium constant `K_(p)` will be
View Solution`4` mol of carbon dioxide was heated in `1 dm^(3)` vessel under conditions which produced at equilibrium `25%` dissociation into carbon monoxide and oxygen. The number of moles of carbon monoxide produced
View Solution`1` mol of `N_(2)` is mixed with `3` mol of `H_(2)` in a litre container. If `50%` of `N_(2)` is converted into ammonia by the reaction `N_(2)(g)+3H_(2)(g) hArr 2NH_(3)(g)`, then the total number of moles of gas at the equilibrium are
View SolutionFor reaction : `H_(2)(g)+I_(2)(g) hArr 2HI(g)` at certain temperature, the value of equilibrium constant is `50`. If the volume of the vessel is reduced to half of its original volume, the value of new equilibrium constant will be
View SolutionWhen ethanol and acetic acid are mixed together in equimolar proportions, equilibrium is attained when `2//3rd` of acid and alcohol are consumed. The equilibrium constant for the reaction is
View SolutionFor the reaction `I_(2)(g) hArr 2I(g)`, `K_(c) 37.6 xx 10^(-6)` at 1000K . If 1.0 mole of `I_(2)` is introduced into a 1.0 litre flask at 1000K, at equilibrium
View SolutionThe system `PCl_(5)(g) hArr PCl_(3)(g)+Cl_(2)(g)` attains equilibrium. If the equilibrium concentration of `PCl_(3)(g)` is doubled, the concentration of `Cl_(2)(g)` would become
View Solution`XY_(2)` dissociates `XY_(2)(g) hArr XY(g)+Y(g)`. When the initial pressure of `XY_(2)` is `600` mm Hg, the total equilibrium pressure is `800` mm Hg. Calculate `K` for the reaction assuming that the volume of the system remains unchanged.
View SolutionConsider the reaction
`A(g)+B(g) hArr C(g)+D(g)`
Which occurs in one step. The specific rate constant are `0.25` and `5000` for the forward and reverse reaction, respectively. The equilibrium constant is
View SolutionFor the equilibrium system `2HX(g) hArr H_(2)(g)+X_(2)(g)` the equilibrium constant is `1.0xx 10^(-5)`. What is the equilibrium concentration of HX if the equilibrium concentrations of `H_(2)` and `X_(2)` are `1.2xx10^(-3) M` and `1.2 xx 10^(-4) M` respectively ?
View SolutionFor the reactions
`A hArr B, K_(c ) =1`
`B hArr C, K_(c)=2`
`C hArr D, K_(c)=3`
`K_(c)` for the reaction `A hArr D` is
View SolutionThe rate constans of forward and backward reactions are `8.5 xx 10^(-5)` and `2.38 xx 10^(-4)` respectively. The equilibrium constant if
View SolutionThe vapour density of `N_(2)O_(4)` at a certain temperature is `30`. Calculate the percentage dissociation of `N_(2)O_(4)` this temperature.
View SolutionThe vapour density of `Pcl_(5)` is `104.16` but when heated to `230^(@)C`, its vapour density is reduced to `62`. The degree of dissociation of `PCl_(5)` at `230^(@)C` is …………
View SolutionThe rate of the elementary reaction
`H_(2)(g) +I_(2)(g) hArr 2HI(g) ` at `25^(@)C` is given by `:`
Rate `=1.7xx10^(-18) [H_(2)][I_(2)]`
The rate of decomposition of gaseous `HI` to `H_(2)(g)` and `I_(2)(g)` at `25^(@)C` is Rate`=2.4xx10^(-21)[HI]^(2)`
Equilibrium constant for the formation of one mole of gaseous `HI` from the `H_(2)(g)` and `I_(2)(g)` is `:`
View SolutionIn the following equilibria
`I:A+2B hArr C, K_(eq)=K_(1)`
`II: C+DhArr 3A, K_(eq)=K_(2)`
`III, 6B+D hArr 2C, K_(eq)=K_(3)`
Hence,
View SolutionConsider following reactions is equilibrium with equilibrium concentration 0.01M of every species `:`
`I:PCl_(5) hArr PCl_(3)+Cl_(2)`
`II: H_(2)+I_(2)hArr 2HI`
`III: N_(2)+3H_(2)hArr 2NH_(3)`
Extent of the reactions taking place is `:`
View SolutionThe equlibrium constant `K_(c)` for the reaction of `H_(2)` with `I_(2)` is 57.0 at 700K
`H_(2)(g)+I_(2)(g)underset(k_(b))overset(k_(f))(hArr) 2HI, K_(c)=57` at 700K Select correct statement `:`
View SolutionNaphthalene, a white solid used to make mothballs, has a vapour pressure of 0.10 mm Hg at `27^(@)C`. Hence `K_(p)` and `K_(c)` for the equilibruim are `: C_(10)Hg(s)hArr C_(10)Hg(g)`
View SolutionFor the following equilibrium
`N_(2)O_(4)(g)hArr 2NO_(2)(g)`
`K_(p)` is found to be equal to `K_(c)`. This is attained when `:`
View SolutionFor the following gaseous equilibria X,Y and Z at 300K
`X:2SO_(2)(g)+O_(2)(g)hArr 2SO_(3)(g)`
`Y: PCl_(5)(g)hArr PCl_(3)(g)+Cl_(2)(g)`
`Z : 2HI(g) hArr H_(2)(g)+I_(2)(g)`
ratio of `K_(p)` and `K_(c)` in the increasing order is `:`
View SolutionFor the following equilibrium
`PCl_(5)(g) hArr PCl_(3)(g)+Cl_(2)(g)`
`K_(p)` is formed to be equal to `K_(x )`. This is attained at
View SolutionFor the reactions `:`
`I: CaCO_(3)(s)hArr CaO(s)+CO_(2)(g),P_(CO_(2))=2 "atm"`
`II: CO_(2)(g)+C(s)hArr 2CO_(g),K=6 "atm"`
Hence, equilibrium constnat, `K_(p)` ( in the same units ) for the reaction
`CaCO_(3)(s)+C(s)hArr CaO(s)+2CO(g)` is
View SolutionFor the equilibrium `:`
`I: C_(6)H_(5)COOH+H_(2)OhArr C_(6)H_(5)COO^(-)+H_(3)O^(+),K_(1)=6.30xx10^(-5)`
`II: C_(6)H_(5)COOH+OH^(-)hArrC_(6)H_(5)COO^(-)+H_(2)O, K_(2)=6.30xx10^(9)`
`III: H_(2)O+H_(2)OhArr H_(3)O^(+)+OH^(-), K_(3)=?`
`K_(3)` using above equilibria is` :`
View SolutionIf `beta_(1),beta_(2)` and `beta_(3)` are stepwise formation constants of MCl, `MCl_(2), MCl_(3)` and K is the overall formation constant of `MCl_(3)`, then ( charges omitted) `:`
View Solution`N_(2)+3H_(2)hArr 2NH_(3)`. This is gaseous phase reaction taking place in 1L flask at `127^(@)C`. Starting with 1 mole `N_(2)` and 3 moles `H_(2)`, equilibrium required 500mL of 1M HCl. Hence `K_(c)` is approximately
View SolutionFor the reaction `A+B hArr C+D` taking place in a 1 L vessel, equilibrium concentration of `[C]=[D]=0.5M` if we start with 1 mole each A and B. Percentage of A converted into C if we start with 2 moles of A and 1 mole of B, is
View SolutionEquilibrium constant, `K` changes with temperature. At `300` K, equilibrium constant is `25` and at `400` K it is `10`. Hence, backward reaction will have energy of activation
View SolutionFor the reaction
`NH_(2)COONH_(4)(g)hArr 2NH_(3)(g)+CO_(2)(g)` the equilibrium constant `K_(p)=2.92xx10^(-5)atm^(3)`. The total pressure of the gaseous products when 1 mole of reactant is heated, will be
View Solution`I_(2)+I^(ɵ)hArrI_(3)^(ɵ)`
This reaction is set-up in aqueous medium. We start with `1` mol of `I_(2)` and `0.5` mol of `I^(ɵ)` in `1 L` flask. After equilibrium reached, excess of `AgNO_(3)` gave `0.25` mol of yellow precipitate. Equilibrium constant is
View SolutionVolume of the flask in which species are transferred is double of the earlier flask. In which of the following cases, equilibrium will be shifted in the forward direction ?
View SolutionOne mole each of A and B and 3 moles each of C and D are placed in 11L flask, if equilibrium constant is 2.25 for `A+B hArr C+D` equilibrium concentration of A and C will be in the ratio `:`
View Solution`2SO_(2)+O_(2)hArr 2SO_(3)`. Starting with 2 moles `SO_(2)` and 1 mole `O_(2)` in 1L flask, mixture required 0.4 mole `MnO_(4)^(-)` in acidic medium. Hence, `K_9c)` is
View SolutionFor the reaction `PCl_(5)hArr PCl_(3)+Cl_(2)` in gaseous phase, `K_(c)=4`. In a 2L flask, there are 2 moles each of `PCl_(3)` and `Cl_(2)` and 0.5 mole of `PCl_(5)` . Equilibrium concentration of `PCl_(5)` is
View SolutionFor `N_(2)+3H_(2)hArr 2NH_(3)`, 1 mole `N_(2)` and 3 mol `H_(2)` are at 4 atm. Equilibrium pressure is found to be 3 atm. Hence, `K_(p)` is
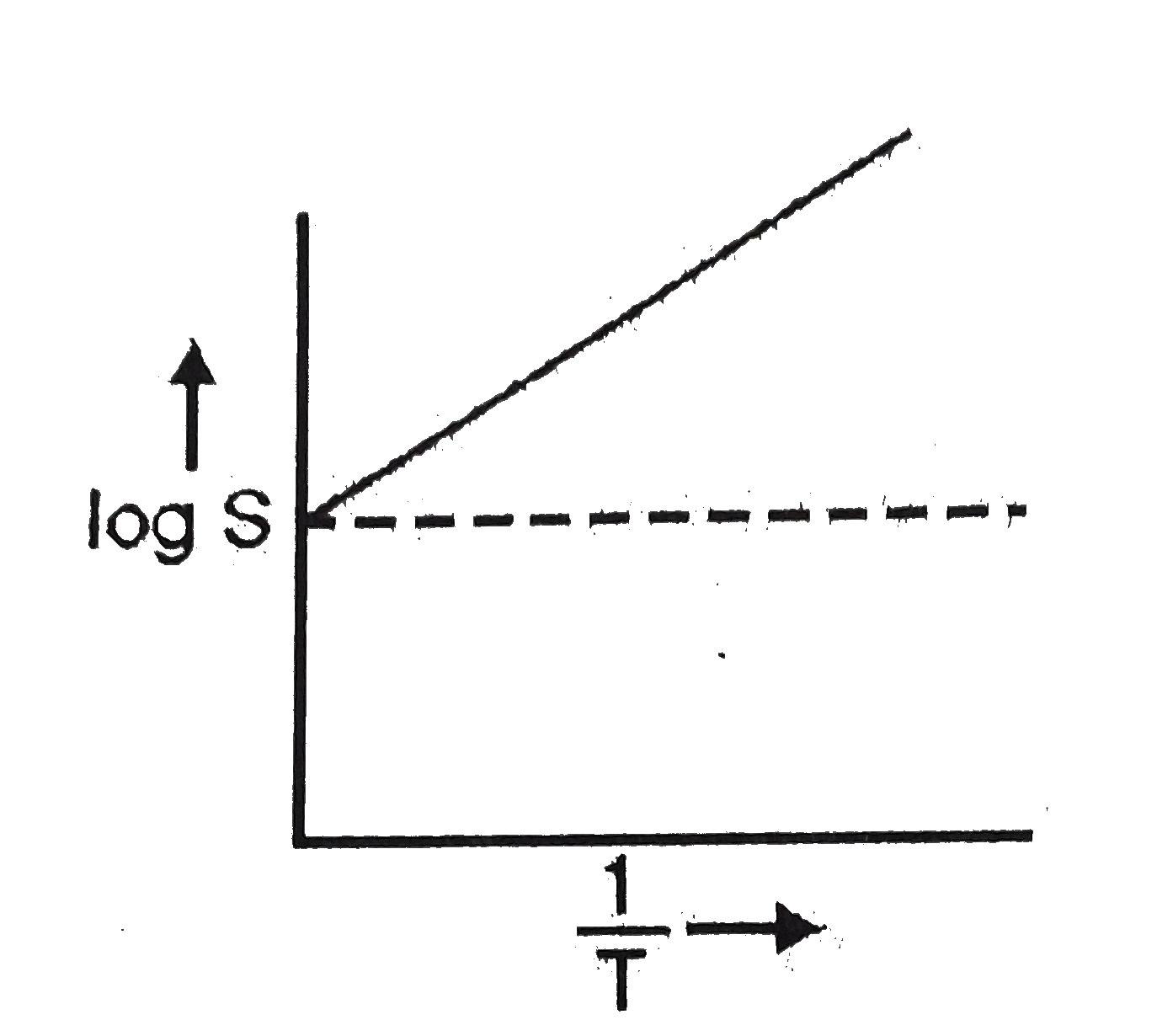
View SolutionSolubility (S) of a solution in a solvent (say `H_(2))` is dependent on temperature as given by `S=Ae^(-Delta//RT)` where `DeltaH` is enthalpy of solution, Solute `+H_(2)OhArr ` solution`, DeltaH=+- x`
For a given solution, variation of log S with temperature is shown graphically. Hence, solute is
View Solution`Hg_(2)Cl_(2)(g)` in saturated aqeous solution has equilibrium constant equal to `:`
View SolutionThe binding of oxygen by haemoglobin (Hb) giving oxy-haemoglobin `(HbO_(2))`, is partially regulated by the concentration of `H_(3)O^(+)` and dissolved `CO_(2)` in blood
`HbO_(2)+H_(2)O^(+)+CO_(2)hArr H^(+)Hb-CO_(2)+O_(2)+H_(2)O` If there is production of lactive acid and `CO_(2)` in a muscle during exertion, then `:`
View SolutionFor the reversible reaction equilibrium is `N_(2)(g)+O_(2)(g)underset(k_(2))overset(k_(1))(hArr)2NO(g)` `C_(0)=Ce^(-2.1xx10^(3))`for the forward and `C_(0)^(')=C^(')e^(-4.2xx10^(-4t))`for the backward reaction, hence, `K_(c)` for the above equilibrium is (both forward and backward reactions are first order reactions )
View SolutionFor the equilibrium in a closed vessel`" "PCl_(5)(g) hArr PCl_(3)(g)+Cl_(2)(g)`,
`K_(p)` is found to be double of `K_(e)` . This is attained when `:`
View SolutionFor the equilibrium `2H_(2)O(g) hArr 2H_(2)(g)+O_(2)(g)`, equilibrium constant is `K_(1)`
For the equilibrium `2CO_(2)hArr 2CO(g)+O_(2)(g) `, equilibrium constant is `K_(2)`
The equilibrium constant for `:`
`CO_(2)(g)+H_(2)(g)hArr CO(s)+H_(2)O(g)` is `:`
View SolutionFor the following equilibrium reaction `N_(2)O_(4)(g)hArr 2NO_(2)(g)`, `NO_(2)` is 50% of the total volume at a given temperature. Hence, vapour density of the equilibrium mixture is `:`
View SolutionThere is 50% dimer formation of benzoic acid `(C_(6)H_(5)COOH)_(2)` in benzene solution. `2C_(6)H_(5)COOHhArr (C_(6)H_(5)COOH)_(2)`. Hence abnormal molecular weight of benzoic acid (theorectical value `=122g mol^(-1))` is
View SolutionIn the dissociation of `N_(2)O_(4)` into `NO_(2). (1+x)` values with the vapour densities ratio `((D)/(d))` is given by `:`
View SolutionFor the dissociation of `PCl_(5)` into `PCl_(3)` and `Cl_(2)` in gaseous phase reaction , if d is the observed vapour density and D the theoretical vapour density with `'alpha'` as degree of dissociation ,variaton of D/d with `'alpha'` is given by ?
View SolutionFor a very small extent of dissociation of `PCl_(5)` into `PCl_(3)` and `Cl_(2)` is a gaseous phase reaction then degree of dissociation , x `:`
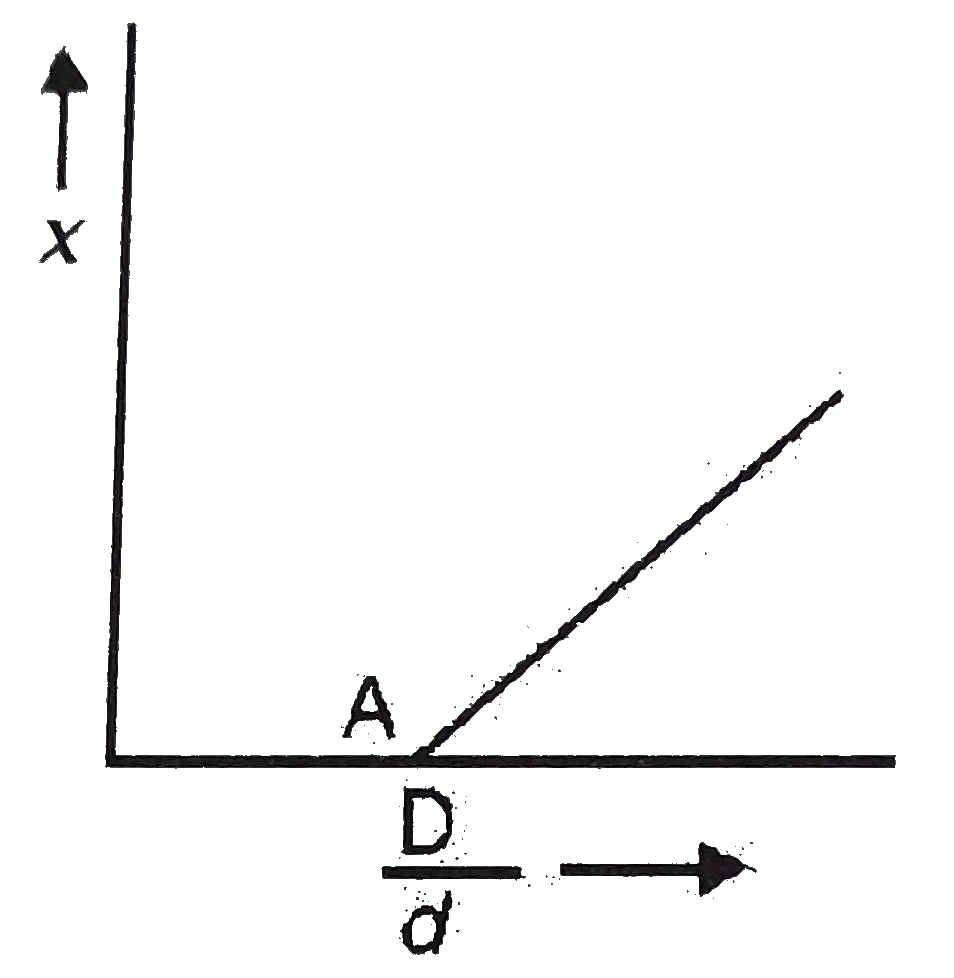
View SolutionBefore equilibrium is set-up for the chemical reaction, `N_(2)O_(4)hArr 2NO_(2)`, vapour density of the gaseous mixture was measured. If D is the theoretical value of vapour density, variation of x with `D//d` is by the graph.
View Solution1 mole each of `CO(g), H_(2)O(g), H_(2)(g)` and `CO_(2)(g)` are placed in one placed in one litre flask at `25^(@)C`. When following equilibrium is set -up `CO(g)+H_(2)O(g)hArr CO_(2)(g)+H_(2)(g)`
`K_(p)=0`. Hence `CO_(2)` present at equilibrium is `:`
View Solution60g `CH_(3)COOH` and 46g `C_(2)H_(5)OH` react in 5L flask to form 44g `CH_(3)COOC_(2)H_(5)` at equilibrium. On taking 120 g `CH_(3)COOH` and 46g `C_(2)H_(5)OH, CH_(3)COOC_(2)H_(5)` formed at equilibrium is `:`
View SolutionOne mole of `N_(20O_(4)(g)` at 300K is kept in a closed container under one atmosphere. It is heated to 600K when 20% of `N_(2)O_(4)(g)` is converted to `NO_(2)(g)`
`N_(2)O_(4)hArr 2NO_(2)(g)` Hence resultant pressure is `:`
View SolutionFor the equilibrium `2SO_(2)+O_(2)hArr 2SO_(3)` we start with 2 moles of `SO_(2)` and 1 mole of `O_(2)` at 3 atm. When equilibrium is attained, pressure changes to 2.5atm. Hence, `K_(p)` is `:`
View SolutionSulphide ion `(S^(2-))` reacts with solid sulphur forming `S_(2)^(2-)` and `S_(3)^(2-)` with formation constants 12 and 132 respectively. Formation constant of `S_(3)^(2-)` from sulphur and `S_(2)^(2-)` is `:`
View SolutionThe equilibrium constant for the reaction `H_(3)BO_(3) +` glycerin `hArr (H_(3)BO_(3)` glycerine ) is 0.90. Glycerine present per litre of 0.1 M `H_(3)BO_(3)` to convert `60%` of `H_(3)BO_(3)` into `(H_(3)BO_(3)` glycerine ) is `:`
View Solution1 mole of `PCl_(5)` taken at 5 atm, dissociates into `PCl_(3)` and `Cl_(2)` to the extent of 50%
`PCl_(5)(g)hArr PCl_(3)(g)+Cl_(2)(g)` Thus `K_(p)` is `:`
View SolutionFor the following equilibrium `N_(2)O_(4) hArr 2NO_(2)` `K_(c)=0.67`. If we start with 3 moles of `NO_(2)` and 1 mole of `N_(2)O` in 1L flask, then `NO_(2) ` present at equilibrium is `:`
View Solution`CaCO_(3)(s) hArr CaO(s)+CO_(2)(g)`
For the equilibrium , it is found that
`log K_(p)=8-(6400(K))/(T)`
`T=527^(@)C` if `:`
View SolutionFor the following equilibrium `:`
`NH_(2)CO_(2)NH_(4)(s)hArr 2NH_(3)(g)+CO_(2)(s)`
`K_(p)` is found to be 0.5 at 4400 K . Hence, partial pressure of `NH_(3)` and `CO_(2)` are respectively `:`
View SolutionIn each of the following, total pressure set - up at equilibrium is assumed to be equal and is P atm with equilibrium constants `K_(p)` given `:`
`I: CaCO_(3)(s)hArr CaO(s)+CO_(2)(g),K_(1)`
`II : NH_(4)HS(s)hArr NH_(3)(g)+H_(2)S(g),K_(2)`
`III : NH_(2)CO_(2)NH_(4)(s)hArr 2NH_(3)(g) +CO_(2)(g),K_(3)`
In the increasing order `:`
View SolutionFor the equilibrium `CuSO_(4)xx5H_(2)O(s)hArrCuSO_(4)xx3H_(2)O(s) + 2H_(2)O(g)`
`K_(p) = 2.25xx10^(-4)atm^(2)` and vapour pressure of water is `22.8` torr at 298 K. `CuSO_(4)` . `5H_(2)O(s)` is efflorescent (i.e., losses water) when relative humidity is :
View SolutionAt what relative humidity with `Na_(2)SO_(4)` be deliquescent (absorb moisture) when exposed to the air at `0^(@ )C` ? Given
`Na_(2)SO_(4).10H_(2)O(s) hArr Na_(2)SO_(4)(s) +10H_(2)O(g), K_(p)=4.08xx10^(-25)` and vapour pressure of water at `0^(@)C =4.58` Torr ?
View Solution
Multiple CHOICE QUESTIONS [Based on Numerical Problems] questions and complete solutions for chapter PHYSICAL AND CHEMICAL EQUILIBRIA of S DINESH & CO CHEMISTRY (HINGLISH) of Class 11
All Exercises from DINESH OBJECTIVE CHEMISTRY Class 11 CHEMISTRY PHYSICAL AND CHEMICAL EQUILIBRIA
- LINKED COMPREHENSION TYPE MCQ s (Comprehension 1)
- MATRIX MATCH TYPE MCQs
- MCQs with only one correct answer
- MULTIPLE CHOICE QUESTIONS
- Multiple CHOICE QUESTIONS [Based on Numerical Problems]
- REASON ASSERTION TYPE MCQs
- REVISION QUESTION FROM COMPETITIVE EXAMS
- SELECTED STRAIGHT OBJECTIVE TYPE MCQs
- ULTIMATE PREPARATORY PACKAGE