Complete Solutions to physics of chapter MOTION IN A STRAIGHT LINE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| DISHA | physics |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
A particle starts moving rectilinearly at time `t=0` such that its velocity `v` changes with time `t` according to the equation `v=t^(2)-t`, where `t` is in seconds and `v` in `ms^(-1)`. Find the time interval for which the particle retards.
View SolutionThe co-ordinates of a moving particle at anytime 't' are given by ` x = alpha t^(3) and y = beta t^(3)`. The speed of the particle at time 't' is given by
View SolutionIf a car covers `(2)/(5)^(th)` of the total distance with `v_1` speed and `(3)/(5)^(th)` distance with `v_2`. Then average speed is
View SolutionChoose the correct statements from the following.
View SolutionA particle located at `x = 0` at time `t = 0`, starts moving along with the positive ` x-direction` with a velocity 'v' that varies as ` v = a sqrt(x)`. The displacement of the particle varies with time as
View SolutionFigure here gives the speed-time graph for a body. The displacement travelled between t = 1.0 second and t = 7.0 second is nearest to
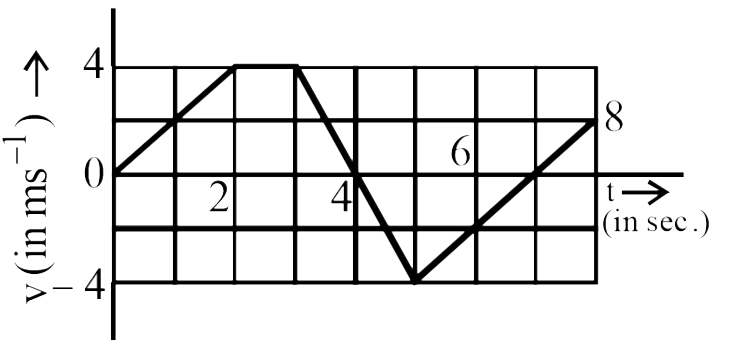
View SolutionA particle is moving in a straight line with initial velocity `u` and uniform acceleration `f`. If the sum of the distances travelled in `t^(th) and (t + 1)^(th)` seconds is `100 cm`, then its velocity after `t` seconds, in `cm//s`, is.
View SolutionA thief is running away on a straight road in a moving with a speed of `9 ms^(-1)`. A policeman chases him on a motor cycle moving at a speed of `10 ms^(-1)`. If the instantaneous separation of the jeep from the motor cycle is `100 m`, how long will it take for the policeman to catch the thief ?.
View SolutionThe displacement x of a particle varies with time according to the relation `x=(a)/(b)(1-e^(-bt))`. Then select the false alternative.
View Solutionmetro train starts from rest and in five seconds achieves a speed 108 km/h. After that it moves with constant velocity and comes to rest after travelling 45m with uniform retardation. If total distance travelled is 395 m, find total time of travelling.
View SolutionThe deceleration exerienced by a moving motor blat, after its engine is cut-off is given by `dv//dt=-kv^(3)`, where `k` is constant. If `v_(0)` is the magnitude of the velocity at cut-off, the magnitude of the velocity at a time `t` after the cut-off is.
View SolutionThe velocity of a particle is `v = v_(0) + g t + ft^(2)`. If its position is ` x=0 ` at ` t= 0 `, then its displacement after unit time `( t = 1 )` is
View SolutionA man is 45 m behind the bus when the bus starts acceleration from rest with acceleration `2.5(m)/(s^2)`. With what minimum velocity should man start running to catch the bus?
View SolutionA body is at rest at ` x =0 ` . At ` t = 0`, it starts moving in the positive `x - direction` with a constant acceleration . At the same instant another body passes through ` x= 0 ` moving in the positive ` x - direction ` with a constant speed . The position of the first body is given by `x_(1)(t)` after time 't', and that of the second body by ` x_(2)(t)` after the same time interval . which of the following graphs correctly describes `(x_(1) - x_(2))` as a function of time 't' ?
View SolutionFrom the top of a multi-storeyed building 40m tall, a boy projects a stone vertically upwards with an initial velocity of` 10 ms^(–1) `such that it eventually falls to the ground.
View SolutionTwo bodies begin to fall freely from the same height but the second falls T second after the first. The time (after which the first body begins to fall) when the distance between the bodies equals L is
View SolutionLet A, B, C, D be points on a vertical line such that AB = BC = CD. If a body is released from position A, the times of descent through AB, BC and CD are in the ratio.
View SolutionWater drops fall at regular intervals from a tap 5 m above the ground. The third drop is leaving the tap, the instant the first drop touches the ground. How far above the ground is the second drop at that instant. `(g = 10 ms^-2)`
View SolutionThe displacement 'x' (in meter) of a particle of mass 'm' (in kg) moving in one dimension under the action of a force is released to time 't' (in sec) by `t = sqrt(x) + 3`. The displacement of the particle when its velocity is zero will be.
View SolutionA body moving with a uniform acceleration crosses a distance of 65 m in the 5 th second and 105 m in 9th second. How far will it go in 20 s?
View SolutionAn automobile travelling with a speed `60 km//h` , can brake to stop within a distance of `20 m` . If the car is going twice as fast i. e. , `120 km//h`, the stopping distance will be
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionThe equation represented by the graph below is :

View SolutionA particle move a distance `x` in time `t` according to equation `x = (t + 5)^-1`. The acceleration of particle is alphaortional to.
View SolutionA particle when thrown, moves such that it passes from same height at 2 and 10 seconds, then this height h is :
View SolutionThe distance through which a body falls in the nth second is h. The distance through which it falls in the next second is
View SolutionA stone is thrown vertically upwards with an initial speed `u` from the top of a tower, reaches the ground with a speed `3 u`. The height of the tower is :
View SolutionA particle moves along a straight line `OX`. At a time `t` (in seconds) the distance `x` (in metre) of the particle is given by `x = 40 +12 t - t^3`. How long would the particle travel before coming to rest ?
View SolutionThe graph below shws the velocity versus time graph for a body
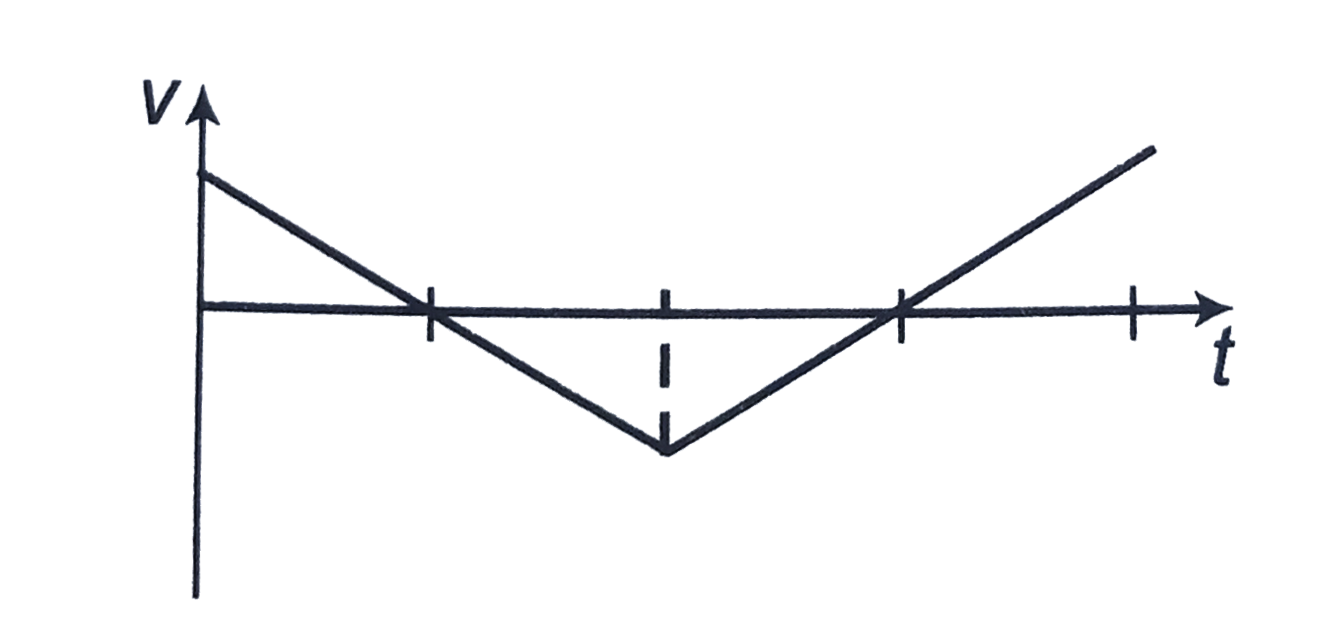
Which of the following graph represents the corresponding acceleration v//s time graph?
View SolutionA particle moving along x-axis has acceleration `f`, at time `t`, given by `f = f_0 (1 - (t)/(T))`, where `f_0` and `T` are constant.
The particle at `t = 0` has zero velocity. In the time interval between `t = 0` and the instant when `f = 0`, the particle's velocity `(v_x)` is :
View SolutionA ball is thrown vertically up with a velocity `u`. It passes three points `A, B` and `C` in its upward journey with velocities `u/s,u/3` and `u/4`, respectively. Find `(AB)/(BC)`.
View SolutionA boat takes two hours to travel 8 km and back in still water. If the velocity of water is 4 km/h, the time taken for going upstream 8 km and coming back is
View SolutionA body starts from rest and travels a distance x with uniform acceleration, then it travels a distance 2x with uniform speed, finally it travels a distance 3x with uniform retardation and comes to rest. If the complete motion of the particle is along a straight line, then the ratio of its average velocity to maximum velocity is
View SolutionA man of `50 kg` mass is standing in a gravity free space at a height of `10m` above the floor. He throws a stone of `0.5 kg` mass downwards with a speed `2m//s`. When the stone reaches the floor, the distance of the man above the floor will be
View SolutionA boy moving with a velocity of `20 km h^(–1)` along a straight line joining two stationary objects. According to him both objects
View SolutionA rubber ball is dropped from a height of `5m `on a plane, where the acceleration due to gravity is not shown. On bouncing it rises to `1.8 m.` The ball loses its velocity on bouncing by a factor of
View SolutionA stone falls freely from rest from aheight `h` and it travels a distance `9h//25` in the last second. The value of `h` is
View SolutionWhich of the following equation represents the motion of a body moving with constant finite acceleration ? In these equation, y denotes the displacement in time t and p.q and r the arbitary constants ?
View SolutionA particle travels half the distance with a velocity of `6 ms^(–1)`. The remaining half distance is covered with a velocity of `4 ms^(–1)` for half the time and with a velocity of `8 ms^(–1)` for the rest of the half time. What is the velocity of the particle averaged over the whole time of motion ?
View SolutionA bullet is fired with a speed of 1000 m/sec in order to penetrate a target situated at 100 m away. If `g = 10 m//s^(2)`, the gun should be aimed
View SolutionA body covers 26, 28, 30, 32 meters in 10^(th), 11^(th), 12^(th) and 13^(th) seconds respectively. The body starts
View SolutionA particle is moving with uniform acceleration along a straight line. The average velocity of the particle from P to Q is `8ms^(–1)` and that Q to S is `12ms^(–1)`. If QS = PQ, then the average velocity from P to S is

View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
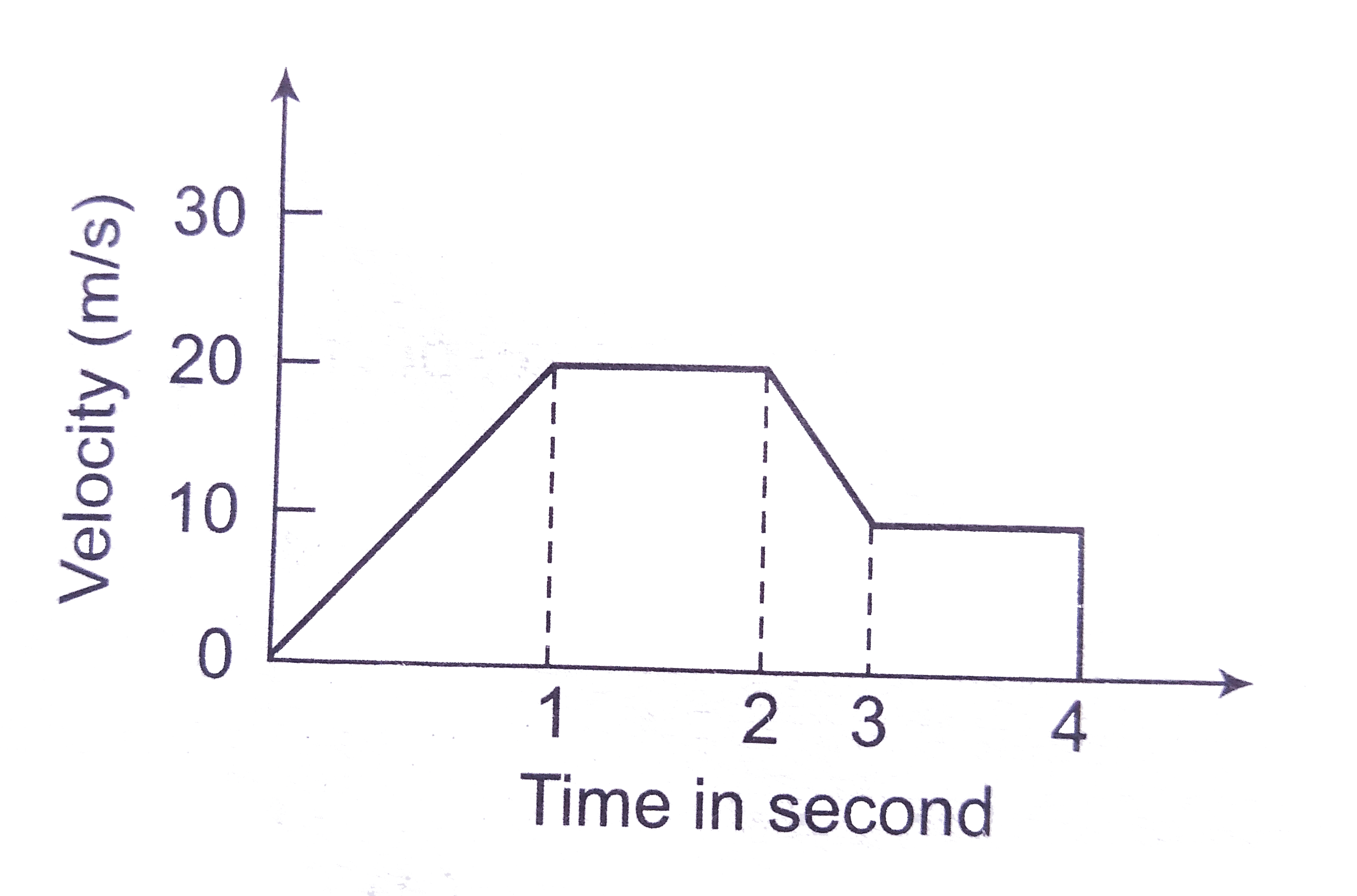
View SolutionA stone falls freely under gravity. It covered distances `h_1, h_2` and `h_3` in the first `5` seconds. The next `5` seconds and the next `5` seconds respectively. The relation between `h_1, h_2` and `h_3` is :
View SolutionA car , starting from rest, accelerates at the rate `f` through a distance `S` then continues at constant speed for time `t` and then decelerates at the rate `(f)/(2)` to come to rest . If the total distance traversed is `15 S` , then
View Solution
physics questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of DISHA PHYSICS (HINGLISH) of Class 11