Complete Solutions to PHYSICS of chapter MOTION IN A PLANE of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| DISHA | PHYSICS |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
A projectile is given an initial velocity of ` ( hat(i) + 2 hat (j) ) m//s`, where ` hat(i)` is along the ground and `hat (j)` is along the vertical . If ` g = 10 m//s^(2) `, the equation of its trajectory is :
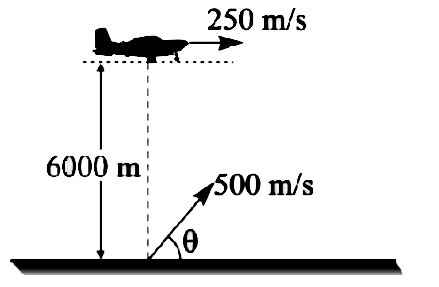
View SolutionAn aircraft moving with a speed of 250 `m//s` is at a height of 6000 m, just overhead of an anti aircraft–gun. If the muzzle velocity is 500 `m//s` the firing angle `theta` should be:
View SolutionTwo racing cars of masses `m_(1)` and `m_(2)` are moving in circles of radii `r_(1)` and `r_(2)` respectively. Their speeds are such that each makes a complete circle in the same duration of time t. The ratio of the angular speed of the first to the second car is
View SolutionA boy playing on the roof of a `10 m` high building throws a ball with a speed of `10 m//s` at an angle of `30(@)` with the horizontal. How far from the throwing point will the ball be at the height of `10 m` from the ground ?
`[ g = 10m//s^(2) , sin 30^(@) = (1)/(2) , cos 30^(@) = (sqrt(3))/(2)]`
View SolutionA bomber plane moves horizontally with a speed of `600 m//s` and a bomb released from it, strikes the ground in `10 s`. The angle with horizontally at which it strikes the ground will be
View SolutionTwo particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if `alpha ` is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
View SolutionInitial velocity with which a body is projected is 10 `m//sec` and angle of projection is `60^(@)`. Find the range R

View SolutionThe position vectors of points A,B,C and D are `A=3hati+4hatj+5hatk`,`B=4hai+5hatj+6hatk`,`C=7hati+9hatj+3hatk`, and `D=4hati+6hatj`, then the displacement vectors AB and CD are
View SolutionA person aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of `0.5(m)/(s)` at an angle of `120^@` with the direction of flow of water. The speed of water in the stream is
View SolutionA projectile thrown with velocity v making angle `theta` with vertical gains maximum height H in the time for which the projectile remains in air, the time period is
View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of `theta` . From the same point and at the same instant , a person starts running with a constant speed `('v_(0)')/(2) ` to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection `theta` ?
View SolutionIf Vectors `vec(A)= cos omega hat(i)+ sin omega hat(j)` and `vec(B)=(cos)(omegat)/(2)hat(i)+(sin)(omegat)/(2)hat(j)`are functions of time. Then the value of `t` at which they are orthogonal to each other is
View SolutionA bus is moving on a straight road towards north with a uniform speed of 50 `km//hour` turns through `90^(@)`. If the speed remains unchanged after turning, the increase in the velocity of bus in the turning process is
View SolutionThe velocity of projection of oblique projectile is `(6hati+8hatj)ms^(-1)` The horizontal range of the projectile is
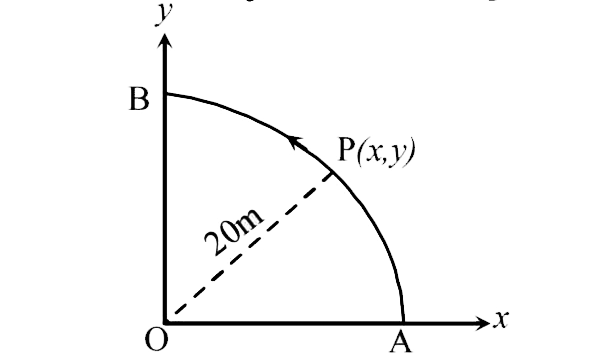
View SolutionA point `p` moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length `s = t^(3) + 5 ` , where `s` is in metres and ` t` is in seconds . The radius of the path is `20 m` . The acceleration of 'P' when ` t = 2 s` is nearly .
View SolutionThe resultant of two vectors `vecA` and `vecB` is perpendicular to the vector `vecA` and its magnitude is equal to half of the magnitude of the vector `vecB`. Find out the angles between `vecA` and `vecB`.
 .
.
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle `theta` to the vertical. The velocity of rain with respect to the ground is :
View SolutionTwo projectiles A and B thrown with speeds in the ratio 1 : `sqrt(2)` acquired the same heights. If A is thrown at an angle of `45^(@)` with the horizontal, the angle of projection of B will be
View SolutionA projectile can have the same range 'R' for two angles of projection . If `'T_(1)'` and `'T_(2)'` to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .
View SolutionA man standing on the roof a house of height `h` throws one particle vertically downwards and another particle horizontally with same velocity `u`. Find the ratio of their velocities when they reach the earth's surface.
View SolutionIf a unit vector is represented by `0.5hati + 0.8hatj + chatk` the value of c is
View SolutionAn aeroplane is flying in a horizontal direction with a velocity `600 km//h` at a height of 1960 m. When it is vertically above the point A on the ground, a body is dropped from it. The body strikes the ground at point B. Calculate the distance AB.
View SolutionA particle is projected with a velocity `v` so that its range on a horizontal plane is twice the greatest height attained. If `g` is acceleration due to gravity, then its range is
View SolutionTwo particles are projected with same speed but at angles of projection `(45^(@)-theta)` and `(45^(@)+theta)`. Then their horizontal ranges are in the ratio of
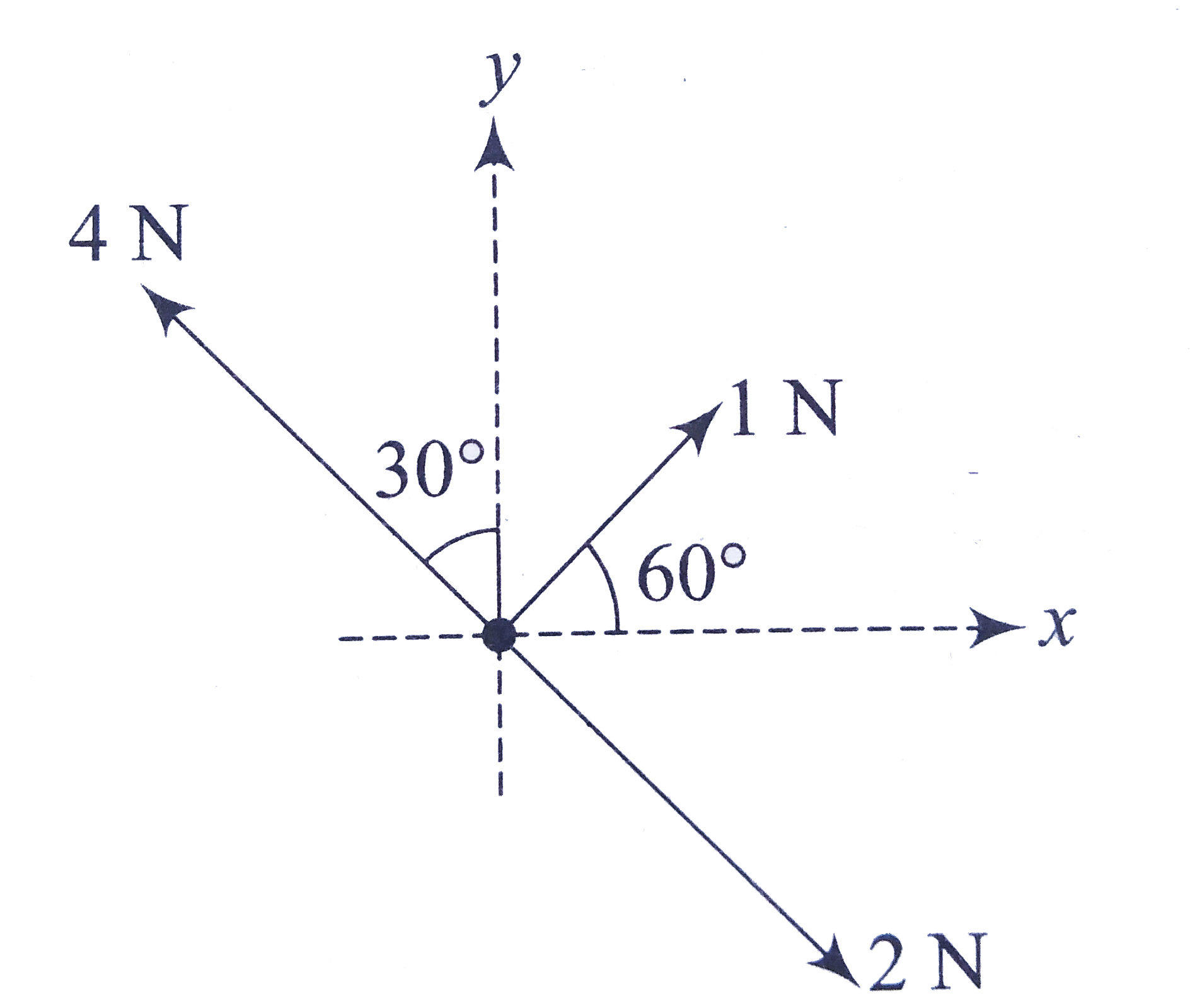
View SolutionThree forces acting on a body are shown in figure. To have the resultant force only along the y-directon, the magnitude of the minimum additional force needed si
View SolutionA particle moves in the `x-y` plane under the action of a force `vecF` such that the value of its linear momentum `vecP` at any time `t is P_(x) = 2 cos t, P_(y) = 2 sin t`.
The angle `theta` between vecF and vecP` at a given time `t` will be:
View SolutionA person sitting in the rear end of the compartment throws a ball towards the front end. The ball follows a parabolic path. The train is moving with uniform velocity of `20ms^(-1)`. A person standing outside on the ground also observers the ball. How will the maximum heights `(h_(m))` attained and the ranges (R) seen by thrower and the outside observer compare each other?
View SolutionIf a particle moves in a circle describing equal angles in equal intervals of time, then the velocity vector.
View SolutionThree identical balls are thrown from the top of a building, all with the same initial speed. As shown in figure., the first ball is thrown horizontally, second above horizontal level, and third at an angle below the horizontal. Neglecting air resistance, rank the speeds of the balls at the instant each hits the ground.

View SolutionA particle is moving such that its position coordinates `(x, y)` are `(2m, 3m)` at time `t=0, (6m, 7m)` at time `t=2 s`, and `(13 m, 14m)` at time `t=5 s`.
Average velocity vector`(vec(V)_(av))` from `t=0` to `t=5 s` is
View SolutionA particle moves so that its position vector is given by `vec r = cos omega t hat x + sin omega t hat y`, where `omega` is a constant which of the following is true ?
View SolutionTwo boys are standing at the ends A and B of a ground, where `AB=a`. The boy at B starts running in a direction perpendicular to AB with velocity `v_(1)`. The boy at A starts running simultaneously with velocity v and catches the other boy in a time t, where t is :
View SolutionA projectile is fired at an angle of `45^(@)` with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
View SolutionThe position vector of a particle `vec(R )` as a funtion of time is given by:
`vec(R )= 4sin(2pit)hat(i)+4cos(2pit)hat(j)`
Where `R` is in meters, `t` is in seconds and `hat(i)` and `hat(j)` denote until vectors along x-and y- directions, respectively Which one of the following statements is wrong for the motion of particle ?
View SolutionThe vectors`vecA` and `vecB` uur are such that |`vecA + vecB`| =|`vecA-vecB `|The angle between the two vectors is
View SolutionThe velocity of projection of oblique projectile is `(6hati+8hatj)ms^(-1)` The horizontal range of the projectile is
View SolutionAn artillary piece which consistently shoots its shells with the same muzzle speed has a maximum range R. To hit a target which is `R//2` from the gun and on the same level, the elevation angle of the gun should be
View SolutionA car runs at a constant speed on a circular track of radius 100m, taking 62.8s for every circular loop. The average velocity and average speed for each circular loop respectively is:
View SolutionA vector of magnitude b is rotated through angle `theta`. What is the change in magnitude of the vector?
View SolutionA stone projected with a velocity u at an angle (theta )with the horizontal reaches maximum heights `H_(1)`. When it is projected with velocity u at an angle `(pi/2-theta)` with the horizontal, it reaches maximum height `H_(2)`. The relations between the horizontal range R of the projectile, `H_(1) and H_(2)`, is
View SolutionThe vector sum of two forces is perpendicular to their vector differences. In that case, the forces
View SolutionA particle starts from the origin of coordinates at time t = 0 and moves in the xy plane with a constant acceleration `alpha` in the y-direction. Its equation of motion is `y= betax^2`. Its velocity component in the x-direction is
View SolutionA vector `vecA` ur is rotated by a small angle `triangletheta` radian `(triangletheta ltl)` to get a new vector `barB` In that case `|vecB-vecA|` is:
View SolutionIf a body moving in circular path maintains constant speed of 10 `ms^(–1)`, then which of the following correctly describes relation between acceleration and radius ?
View SolutionThe position of a projectile launched from the origin at t = 0 is given by `vacr`=`(40hati+50hatj)`mat t=2s. if the projectile was launched at an angle `theta` from the horizontal, then `theta`is (take g = 10 `ms^(–2)`
View Solution
PHYSICS questions and complete solutions for chapter MOTION IN A PLANE of DISHA PHYSICS (HINGLISH) of Class 11