Complete Solutions to Problem For Practice of chapter FRICTION AND CIRCULAR MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FRICTION AND CIRCULAR MOTION |
| GRB PUBLICATION | Problem For Practice |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
In the diagram shown, the blocks A, B and C weight, 3kg, 4kg and 5kg respectively. The coefficient of sliding friction between any two surface is 0.25. A is held at rest by a massless rigid rod fixed to the wall while B and C are connected by a light flexible cord passing around a frictionless pulley. Find the force F necessary to drag C along the horizontal surface to the left at constant speed. Assume that the arrangement shown in the diagram, B on C and A on B, is maintained all through. `(g=9.8m//s^2)`
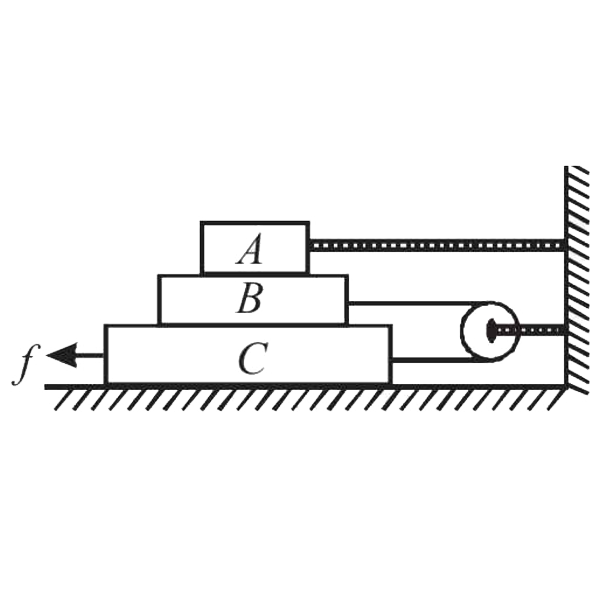 11:46View Solution
11:46View SolutionA 40 kg slab rests on a frictionless floor . A 10 kg block rests on the top of the slab . [Fig. 7.81 (a)] . The coefficients of static and dynamic friction are `0.60` and `0.40` respectively . The 10 kg block is pulled by a horizontal force of 100 N . what are the resulting accelerations of (a) the block (b) the slab ? ( g = `10 m// s^(2)`)
 09:24View Solution
09:24View SolutionA body of mass `M` with a small block `m` placed on it rests on a smooth horizontal surface. The block is set in motion in the horizontal direction with a velocity `v`. To what height relative to the initial level will the block rise after breaking off from the body `M`. Friction can be assumed to be absent.
 10:17View Solution
10:17View SolutionA rock-climber (49 kg) is managing to be at rest between two vertical rocks pressing one rock A by his feet and the other B by his back . If the coefficient of friction between his shoes and wall is A `1.2` while between his back and wall B is `0.8` and limiting friction acts at all the contacts , then : (a) What is his push against the rock ? (b) What percent of the weight is supported by the frictional force an legs ?
 04:55View Solution
04:55View SolutionThe three flat blocks in the figure are positioned on the `30 ^(@)` incline and a force parallel to the inclined plane is applied to the middle block . The upper block is prevented from moving by a wire which attaches it to the fixed support . The coefficient of static friction for each of the three pairs of contact surfaces is shwon in the figure . Determine the maximum value which P may have before any slipping takes place .
 View Solution
View SolutionIn the Fig. 7.85 shown a constant force is applied on the lower block , just large sliding out from between the upper block and the table . Determine the acceleration of each block .
 View Solution
View SolutionA `10kg` block rests on a `5kg` bracket as shown in figureThe `5kg` breaket rests on a horizontal surface The coefficient of frictionbetween the `10kg` block and the braket on wich it rests are `mu_(s) = 0.40 and mu_(k) = 0.30`

If the `10 kg` block is not to slide on the braket , the corresponding acceleration of the `5 kg` braacket is02:47View SolutionA block of mass `0.5` kg rests on a wedge of mass 2 kg as in Fig. 7.87 . The wedge is acted on by a horizontal force F and slides on a frictionless surface . If the coefficient of static friction between the wedge and the block is `mu_(s) = 0.8` , and the angle of inclination is `30^(@)` , find the maximum and minimum values of F for which the block does not slip . Take (g = `10 m//s^(2)`)
 View Solution
View SolutionA solide homogeneous cylinder of height `h` and base radius `r` is kept vertically on a conveyer belt moving horizontally with an increasing velocity `v=a+bt^(2)`. If the cylinder is not allowed to slip then the time whem the cylinder is about to topple , will be equal to
03:10View SolutionIn the Fig 7.89 shown , `m_(2) = 2.5` kg , h = `1.5` m , the system is released from rest at t = 0 and the mass `m_(2)` strikes ground at t = `0.82`s . The system is placed in its initial position and a `1.2` kg mass is placed on top of the block of mass `m_(1)` . Released from rest , the mass `m_(2)` now strikes the ground `1.3` s later . Determine the mass `m_(1)` and the coefficient of kinetic friction between `m_(1)` and the shelf .
 View Solution
View SolutionFigure-2.85 shows a block B of mass m, cart C of mass M, and the coefficient of static between the block and the cart is `mu`. Neglect frictional between wheels and axles and the rotational effects of the wheels. Determine the minimum value of F which must be applied on B such that it will not slide.
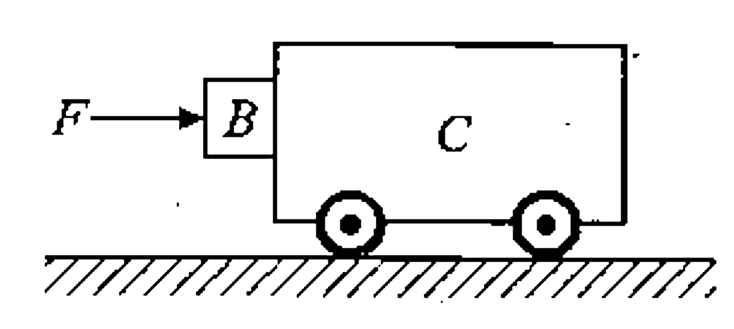
`[(mg)/(mu)(1+(m)/(M))]`02:36View SolutionA block of mass `2.20` kg is accelerated across a rough surface by a rope passing over a pulley as shown in Fig. 7.91 . The tension in the rope is `10.0` N , and the pulley is `10.0` cm above the block . The coefficient of friction is `0.4` .
(a) Determine the acceleration of block when x = `0.4` m .
(b) Find the value of x at which the acceleration becomes zero .
 View Solution
View SolutionA circular disc with a groove along its diameter is placed horizontally . A block of mass 1 kg is placed as shown . The coefficient of friction between the block and all surfaces of groove in contact is `mu = 2//5` . The disc has an acceleration of `25 m//s^(2)` . find the acceleration of the block with respect to disc .
 View Solution
View SolutionA block rests on a rough inclined plane as shown in Fig. 7.93 . A horizontal force is applied to it . (a) Find out the force of reaction .
(b) Can the force of friction be zero ? If yes , when ? (c) Assuming that , friction is not zero , find it magnitude and the direction of its limiting value .
 04:25View Solution
04:25View SolutionFind the acceleration `a_(1) , a_(2) and a_(3)` of the three blocks shown in Fig if a horizontal force of `10 N` is applied on

(a) `2 kg` blocks, (b) `3 kg` blocks and ( c) `7 kg` blocks (Take `g = 10 ms^(-2))`08:46View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity `omega` in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
05:11View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length `3R//4` is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of `60^@` with the vertical. The spring constant `K=mg//R`. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.
 12:25View Solution
12:25View SolutionA circular table with smooth horizontal surface is rotating at an angular speed `omega` about its axis. A groove is made on the surface along a radius and a small particle is gently placed inside the groove at a distance l from the centre. Find the speed of the particle with respect to the table as its distance from the centre becomes L.
01:49View SolutionA metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
04:08View SolutionA particle describes a horizontal circle on the smooth inner surface of a conical funnel as shown in Fig. If the height of the plane of the circle above the vertex is `9.8 cm`, find the speed of the particle.
04:16View SolutionTwo blocks of mass `m_(1)=10kg` and `m_(2)=5kg` connected to each other by a massless inextensible string of length `0.3m` are placed along a diameter of the turntable. The coefficient of friction between the table and `m_(1)` is `0.5` while there is no friction between `m_(2)` and the table. the table is rotating with an angular velocity of `10rad//s`. about a vertical axis passing through its center `O`. the masses are placed along the diameter of the table on either side of the center `O` such that the mass `m_(1)` is at a distance of `0.124m` from `O`. the masses are observed to be at a rest with respect to an observed on the tuntable `(g=9.8m//s^(2))`.
(a) Calculate the friction on `m_(1)`
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on `m_(1)`.05:46View SolutionA piece of ics slides down a `45^(@)` incline in twice the time it takes to slide down a frictionless `45^(@)` incline . What is the coefficient of friction between the ice and the incline ? .
05:50View SolutionA block slides down a rough inclined plane of slope angle `theta` with a constnat velocity. It is then projected up the same plane with an intial velocity v the distance travelled by the block up the plane coming to rest is .
03:42View Solution
Problem For Practice questions and complete solutions for chapter FRICTION AND CIRCULAR MOTION of GR BATHLA & SONS PHYSICS (HINGLISH) of Class 11
