Complete Solutions to worked out examples of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| HC VERMA | worked out examples |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
The lower surface of a slab of stone of face-area `3600cm^(2)` and thickness `10cm` is exposed to steam at `100^(@)C` . A block of ice at `0^(@)C` rests on the upper surface of the slab. `4.8g` of ice melts in one hour. Calculate the thermal conductivity of the stone. Latent heat of fusion of ice `=3.36 xx 10^(5) J kg^(-1)`
View SolutionAn icebox made of 1.5cm thick styrofoam has dimensions `60cmxx60cmxx30cm`.It contains ice at `0^(@)C` and is kept in a room at `40^(@)C`. Find the rate at which the ice is melting. Latent heat of fusion of ice`=3.36xx10^(5)J kg^(-1)` . and thermal conductivity of styrofoam `=0.04Wm^(-1)C^(-1)` .
View SolutionTemperature of water at the surface of lake is – 20°C. Then temperature of water just below the lower surface of ice layer is
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are `K_1` and `K_2`. The temperature of the free ends of the first and second rods are maintained at `θ_1` and `θ_2` respectively. The temperature of the common junction is
View SolutionTwo parallel plates A and B are joined together to form a compound plate . The thicknesses of the plate are `4.0cm` and `2.5cm` respectively and the area of cross section is `100cm^(2)` for each plate. The thermal conductivities are `K_(A)=200Wm^(-1) C^(-1)` for plate A and `K_(B)=400Wm^(-1) C^(-1)` for the plate B. The outer surface of the plate A is maintained at`100^(@)C` and the outer surface of the plate B is maintained at `0^(@)C`. Find (a) the rate of heat flow through any cross section, (b) the temperature at the interface and (c) the equivalent thermal conductivity of the compound plate.

View SolutionThe temperature inside a refrigator is `t_2^@`C and the room temperature is `t_1^@C`. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be
View SolutionAn electric heater is used in a room of total wall area `137m^(2)` to maintain a temperature of `20^(@)C` inside it, when the outside temperature is `-10^(@)C` .The walls have three different layers of materials. The innermost layer is of wood of thickness 2.5cm, the middle layer is of cement of thickness 1.0cm and the outermost layer is of brick of thickness 25.0cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and the celling. The thermal conductivities of wood, cement and brick are `0.125Wm^(-1)C^(-1)` , `1.5Wm^(-1)C^(-1)` . and `1.0Wm^(-1)C^(-1)` respectively.
View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at `60^(@)C` and the junction E at `10^(@)C` , calculate the temperature of the junction B. The thermal conductivity of x is `800Wm^(-1)C^(-1)` and that of y is `400Wm^(-1)C^(-1)` .

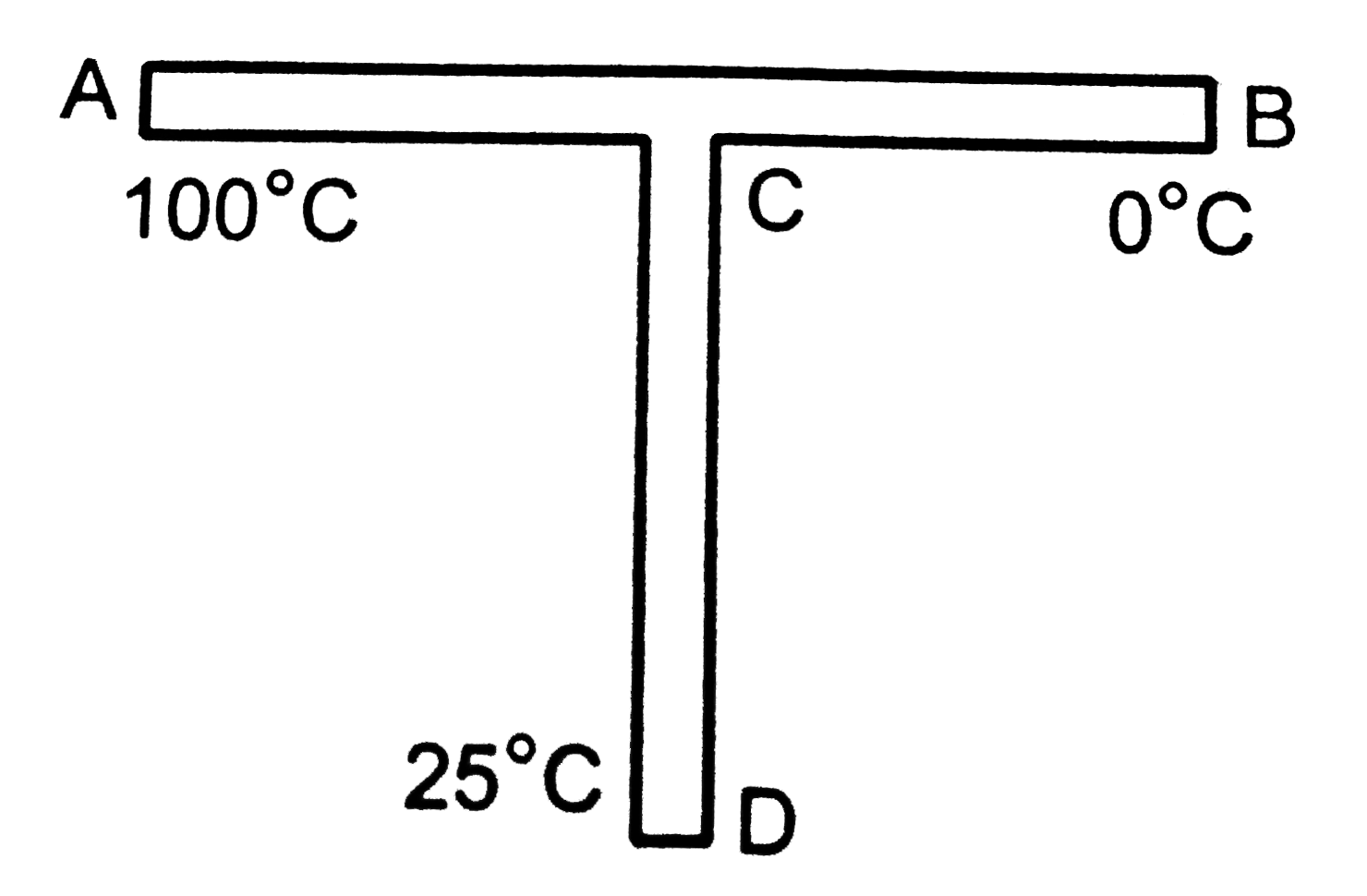
View SolutionA rod CD of thermal resistance `5.0KW^(-1)` is joined at the middle of an identical rod AB as shown in figure. The ends A, B and D are maintained at `100^(@)C` , `0^(@)C` and `25^(@)C` respectively. Find the heat current in CD.
View SolutionTwo thin metallic spherical shells of radii `r_(1)` and `r_(2)` `(r_(1)lt r_(2))` are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature `theta_(1)` .and the outer shell at temperature `theta_(2)` `(theta_(1)lt theta_(2))`. Calculate the rate at which heat flows radially through the material.

View SolutionOn a cold winter day, the atmospheric temperature is `-theta` (on celsius scale) which is below `0^(@)C`. A cylindrical drum of height `h` made of a bad conductor is completely filled with water at `0^(@)C` and is kept outside without any lid. Calculate the time taken for the whole mass of water to freeze. Thermal conductivity of ice is K and its latent heat of fusion is `L`. Neglect expansion of water on freezing.

View SolutionFigure shows a large tank of water at a constant temperature `theta_(0)` and a small vessel containing a mass `m` of water at an initial temperature `theta_1``(lt theta_(0))`. A metal rod of length `L`, area of cross section `A` and thermal conductivity `K` connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become `theta_(2)``(theta_(1)lt theta_(2)lt theta_(0))` . Specific heat capacity of water is `s` and all other heat capacities are negligible.

View SolutionOne mode of an ideal monatomic gas is kept in a rigid vessel. The vessel is kept inside a steam chamber whose temperature is `97^(@)C` . Initially, the temperature of the gas is `5.0^(@)C` . The walls of the vessel have an inner surface of area `800cm^(2)` and thickness `1.0cm` If the temperature of the gas increases to `9.0^(@)C` in `5.0` second, find the thermal conductivity of the material of the walls.
View SolutionA monatomic ideal gas is contained in a rigid container of volume V with walls of total inner surface area A, thickness x and thermal conductivity K. The gas is at an initial temperature `t_(0)` and pressure `P_(0)` . Find the pressure of the gas as a function of time if the temperature of the surrounding air is `T_(s)` . All temperature are in absolute scale.
View SolutionA container contains hydrogen gas at pressure P and temperature T. Another identical container contains helium gas at pressure 2P and temperature `T//2`. The ratio of the number of molecules of the two gases is
View SolutionThe mass of 1 litre of helium under a pressure of 2 atm and at a temperature of `27^(@)C` is
View SolutionAn electric heater emits 1000W of thermal radiation. The coil has a surface area of `0.02m^(2)` . Assuming that the coil radiates like a blackbody, Find its temperature. `sigma=6.0xx10^(-8)Wm^(-2)K^(-2)` .
View SolutionThe light from the sun is found to have a maximum intensity near the wavelength of 470nm. Assuming that the surface o f the sun emits as a blackbody, calculate the temperature of the surface of the sun.
View SolutionA hot water cools from `92^(@)C` to `84^(@)C` in 3 minutes when the room temperature is `27^(@)C`. How long will it take for it to cool from `65^(@)C` to` 60^(@)C`?
View SolutionCooling is transfer of heat energy from the body at higher temperature to lower temperature.
View Solution
worked out examples questions and complete solutions for chapter HEAT TRANSFER of HC VERMA of Class 11