Complete Solutions to SECTION - A of chapter MOCK TEST PAPER-2021 of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MOCK TEST PAPER-2021 |
| VIVA PUBLICATION | SECTION - A |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
If function f defined on th set of integers f(x) = `{{:(1+x,1lexlt2),(2x-1,2lexlt4),(3x-10,4lexlt6):}`
View SolutionIf A,B,C,D are angles of a quadrilateral, then sin A + sin (B+ C + D) = (i) 0 (ii) 1 (iii) 2 (iv) None of these
View Solution`sin 105^(@) + cos 105^(@) = cos theta,` then `theta` =
View Solution`15^(th)` term from end of the sequence 7,10,13,….., 130 is
View SolutionThe coefficient of x in the equation `x^2+px+q=0` was wrongly written as 17 in place of 13 and the roots thus found were -2 and -15. The roots of the correct equation are
(A) `15.-2` (B) `-3,-10` (C) `-13,30` (D) `4,13`
View SolutionIn the binomial expansion of `(1 + x)^(10)`, the coefficeents of `(2m + 1)^(th) and (4m + 5)^(th)` terms are equal. Value of m is
View SolutionIf z is a complex number and `iz^(3) + z^(2) - z + I = 0`, the value of |z| is
View SolutionFind the equation of the bisector of `angle A` of `DeltaABC` whose vertices are A(-2, 4), B(5,5) and C(4,-2) is
View SolutionCircles `x^(2) + y^(2) - 2x = 0 and x^(2) + y^(2) + 6x - 6y + 2 = 0` touch each other extermally. Then point of contact is
View SolutionThe number of proper substes of A, where A = {-3,-1,0,4} is
View SolutionEvaluate: `lim_(xto0)(tan8x)/(sin3x)`
View SolutionIn how many ways can the letters of the word PERMUTATIONS be arranged such that P comes before S.
View Solutionabout to only mathematics
View SolutionIf f(x) = `ax^(3),` show that xf'(x) - 3f(x) = 0.
View SolutionFour persons are selected at random out of 3 men, 2 women and 4 children. The probability that there are exactly 2 children in the selection is a. 11/21 b. 9/21 c. 10/21 d. none of these
View Solutionwhat is Subset of A
View SolutionOut of 500 car owners investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct?
View SolutionProve that: `cos^2A+cos^2B-2cosA\ cos B cos\ (A+B)=sin^2(A+B)`
View SolutionProve that `sin 36^(@) + cos 36^(@) = sqrt(2) cos 9^(@)`
View SolutionProve that `cot 2 theta + tan theta = cosec 2 theta`
View SolutionSimplify `(3 + 2i)^(3)`. Also find its conjugate.
View SolutionIf the roots of the equation `2x^(2) + (k + 1) x + (k^(2) - 5k + 6) = 0` are of opposite signes then show that `2 lt k lt 3.`
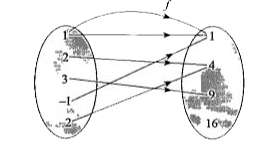
View SolutionWrite the function given by the following diagrams in the ordered pair form. Also write the domain, co-dormain and range. Also classifty the function.
View SolutionIf `cos x = - (1)/(3)`, `x` lies in III quardrnat, then find the values of `sin(x/2), cos (x/2) and tan (x/2)`.
View SolutionProve that `tan [7(1)/(2)]^0 = (sqrt(3) - sqrt(2)) (sqrt(2) - 1)`.
View SolutionProve by the principle of mathematical induction that: `n(n+1)(2n+1)` is divisible by `6` for all `n in Ndot`
View SolutionDifferentiate by `1^(st)`, principle, f(x) = sec (1 - 2x).
View SolutionIf y= `((sqrt(x)+1)(x^(2)-sqrt(x)))/(xsqrt(x)+x+sqrt(x)),` Prove that `(dy)/(dx) = 1`.
View SolutionIf `alpha and beta are the roots of the quadratic equation `x^(2) + px + q = 0`, then form the quadratic equation whose roots are `alpha + (1)/(beta), beta + (1)/(alpha)`
View SolutionBoth roots of equation `x^(2) - (a + 3)x + a + 4 = 0` are negative. Calculate the values of a.
View SolutionThe sum of first four terms of an AP is 56. The sum of the last four terms is 112. If its first term is 11, then find the number of terms. Also find the sum of all terms of the AP.
View SolutionFind the intercepts made by the line 3x + y = 12 on the axes. Also find the equaitons of the straight lines which pass through origin and the trisection of the segment of the line intercepted between the axes.
View Solutionabout to only mathematics
View Solution
SECTION - A questions and complete solutions for chapter MOCK TEST PAPER-2021 of S CHAND MATHS (ENGLISH) of Class 11