Complete Solutions to Example of chapter QUADRATIC EQUATIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | QUADRATIC EQUATIONS |
| S CHAND | Example |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
Solve: `2x^(2)+2x-3=0`, giving your answer correct to one decimal place.
View SolutionSolve: `x^(2)+x+1=0`.
View SolutionSolve: `x^((2)/(3))+x^((1)/(3))-2=0`.
View SolutionIf `4^(1+x)+4^(1-x)=10`, find x.
View SolutionIf `sqrt((2x^(2)+x+2)/(x^(2)+3x+1))+2"."sqrt((x^(2)+3x+1)/(2x^(2)+x+2))-3=0`, find x.
View SolutionSolve: `(x+1)(x+2)(x+3)(x+4)+1=0`.
View SolutionExamine the nature of the roots of the equations
(i) `2x^(2)+2x+3=0`
(ii) `2x^(2)-7x+3=0`
(iii) `x^(2)_5x-2=0`
(iv) `4x^(2)-4x+1=0`
View SolutionIf a,b,c are real, then both the roots of the equation (x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0 are always (A) positive (B) negative (C) real (D) imaginary.
View SolutionFor what value of m, are the roots of the equation (3m+1)`x^(2)+(11+m)x+9=0` equal ? Real and unequal ?
View SolutionIf `alpha,beta` are roots of `x^(2)-px+q=0`, find the value of
(i) `alpha^(2)+beta^(2)`
(ii) `alpha^(3)+beta^(3)`
(iii) `alpha-beta`,
(iv) `alpha^(4)+beta^(4)`.
View SolutionIf `alpha and beta` are the roots of `ax^(2)+bx+c=0`, form the equation whose roots are `(1)/(alpha) and (1)/(beta)`.
View SolutionIf `alpha,beta` are the roots of `ax^(2)+bx+c=0`, form that equation whose roots are `(alpha^(2)+beta^(2)),((1)/(alpha^(2))+(1)/(beta^(2)))`.
View SolutionFind the condition that one root of `ax^(2)+bx+c=0` may be four times the other.
View SolutionProve that the condition that one root of `ax^(2)+bx+c=0` may be the square of the other is `b^(3)+a^(2)c+ac^(2)=3abc`.
View SolutionFor which value of k will the equations `x^(2)-kx-21=0 and x^(2)-3kx+35=0` have one common root ?
View SolutionIf `x^(2)+px+q=0` and `x^(2)+qx+p=0` have a common root, prove that either `p=q` or `1+p+q=0`.
View SolutionGraph the expression `x^(2)+x-6`.
View SolutionGraph the expression `4-5x-x^(2)`.
View Solutionstate true or false : - The roots x=0 and x=3 of the equation `2x(x-3)=0` are the x-intercepts of the graph of y=2x(x-3) as shown in the figure.
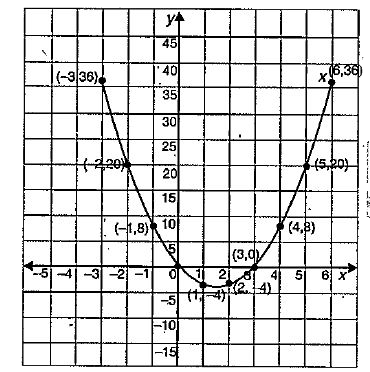
View SolutionState true or false : The two roots x=-5,-5 of the equation `(x+5)^(2)=0` is the x-intercept of the graph of `y=(x+5)^(2)` as shown below.
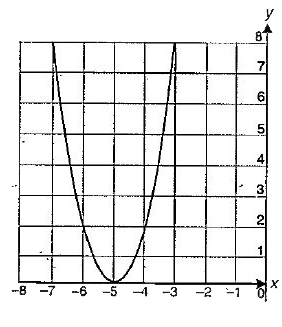 .
.
View SolutionThe graph of the function f(x)=`x^(2)-2x+2` does not touch the x-axis as shown below because the roots are imaginary. Find the roots of the quadratic equation.
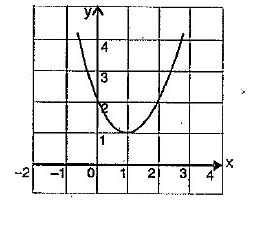 .
.
View Solution(i) Draw a graph of `y=x^(2)-4x+3` for `-2lexle5`.
(ii) Use the graph to solve the equation `x^(2)-4x+3=0`.
View SolutionFind the value of `6x^(2)-5x+1` for all real value of x.
View SolutionDetermine the sign of the function `3x^(2)-2x+1` for real values of x.
View SolutionFind the ranges of the values of x for which `x^(2)-4x+2` lies between -1 and +1.
View SolutionDetermine the value of 'a' so that the expression `x^(2)-2(a+1)x+4, x in R` is always positive.
View SolutionIf x is real, prove that the value of the expression `((x-1)(x+3))/((x-2)(x+4))` cannot be between `(4)/(9) and 1.`
View SolutionIf x be real, find the maximum value of `((x+2))/(2x^(2)+3x+6)`.
View SolutionIf x is real, then find the minimum value of `(x^(2)-x+1)/(x^(2)+x+1)`.
View SolutionIf x is real, the maximum value of `(3x^(2)+9x+17)/(3x^(2)+9x+7)` is
(a) `(17)/(7)`
(b) `(1)/(4)`
(c) 41
(d) 1
View Solution
Example questions and complete solutions for chapter QUADRATIC EQUATIONS of S CHAND MATHS (ENGLISH) of Class 11