Complete Solutions to EXERICSE of chapter MODEL PAPER (5) of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MODEL PAPER (5) |
| JBD PUBLICATION | EXERICSE |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
If A and B are two non-empty sets, then `(A-B)cup(B-A)` is equal to:
View SolutionThe domain of the function `f(x)=(x^2+2x+1)/(x^2-x-6)` is:
View SolutionThe value of `cos75^@` is:
View SolutionThe value of `(1+i)^4+(1-i)^4` is:
View SolutionThe number of arrangements of the letters of the word 'BHARAT' taken all at a time is:
View SolutionIf the sum of n terms of an A.P. is given by `delta_n=3n+2n^2`, then the common difference of an A.P. is
View SolutionThe line segment joining the points (-3,-4) and (1,-2) is divided by y-axis in the ratio:
View SolutionIf the major axis of an ellipse is thrice the minor axis, then its eccentricity is equal to
View Solution`underset(xrarr0)lim (sin2x)/x` is equal to:
View SolutionTwo dice are thrown simultaneously. The probability of obtainng a total score of 5 is,
View SolutionIf `cos (theta + 2alpha) = m cos theta`, prove that : `cot alpha = (1+m)/(1-m)tan(theta + alpha)`.
View SolutionIf `tan(x+y)=20/21, tan (x-y0=3/4`, then show that`tan 2x=143/24`.
View Solutionsimplify: `5i^5+4i^4+3i^3+2i^2+i`
View SolutionExapand: `(2/x-x/2)^(5), x ne 0`
View SolutionFind
3rd term in the expansion of `(3x-y^3/6)^4`.
View SolutionShow that A(a,b,c),B(b,c,a) and C(c,a,b) are the vertices of an equilateral triangle.
View SolutionWrite down the truth value of the following statement:
All integers are natural numbers.
View SolutionWrite down the truth value of the following statement:
Violet are blue.
View SolutionWhich of the following statements are true and which are false?
In each case give a valid reason for your answer.
p: Each radius of a circle is a chord of the circle.
View SolutionIn a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?
View SolutionIf A={3,5},B={2,4,6}. Find
`n(AxxB)`
View SolutionIf A={3,5},B={2,4,6}. Find
`n(BxxA)`
View SolutionProve that: `sin 3x + sin 2x -sin x = 4sin x cosfrac(x)(2)cosfrac(3x)(2)`
View SolutionUsing principle of mathematical induction, prove that:
1+3+5+………..+(2n-1)=`n^2`.
View SolutionA bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
View SolutionFind the value of r if `5. ^4P_r= 6. "^5P_(r-1)`.
View SolutionIf the sum of n terms of an A.P is `nP+1/2 n(n-1)Q`, where P and Q are constant, find the common difference.
View SolutionIf the pth, qth and rth terms of an A.P. be x,y,z repsectively, then show that : `x(q-r)+y(r-p)+z(p-q)=0`
View SolutionFind a point on the x-axis which is equidistant from the points (7, 6) and (3, 4).
View SolutionFind the equation of ellipse that satisfy the given conditions:
Length of minor axis: 16, foci=`(0, pm6)`
View SolutionFind the derivative of `1/x^2`
View SolutionFind `underset(xrarr0)lim f(x)`, where `f(x)={(|x|/x, xne0),(0, x=0):}`
View SolutionOne card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that card drawn is :
i) not an ace
ii) a black card
ii) not a black card
iv) a diamond
v) not a diamond.
View SolutionOne card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that card drawn is :
i) not an ace
ii) a black card
ii) not a black card
iv) a diamond
v) not a diamond.
View SolutionOne card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that card drawn is :
i) not an ace
ii) a black card
ii) not a black card
iv) a diamond
v) not a diamond.
View SolutionIf z=x+iy and |z|=1, show that the complex number `z_1=(z-1)/(z+1)` is purely imagine.
View SolutionSolve the following system of inequalities graphically: `3x + 2y le 12, x ge 1,y ge 2`
View SolutionFind all pairs of consecutive odd natural numbers, both of which are larger than 10, such that their sum is less than 40.
View SolutionIf f(x)= `{:(mx^(2)+n, x lt 0),(nx +m,0le x le 1),(nx^(3) +m, x gt 1):}` For what integers m and n does both `underset(x rarr 0)lim f(x)` and `underset(x rarr 1)lim f(x)` exist
View SolutionFind the derivative of `(secx - 1)/(secx + 1)`
View SolutionFind the mean deviatioan about the mean for the following data:
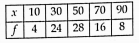
View Solution
EXERICSE questions and complete solutions for chapter MODEL PAPER (5) of JBD PUBLICATION of Class 11