Complete Solutions to EXERCISE of chapter MODEL PAPER (11) of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MODEL PAPER (11) |
| JBD PUBLICATION | EXERCISE |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
The set `(A cap B')' cup (BcapC)` is equal to:
View SolutionDomain of `sqrt(a^2-x^2)` (a>0) is:
View Solution`sin36^@ sin72^@ sin108^@ sin144^@` is equal to:
View SolutionThe value of `(1+i)^3-(1-i)^3` is:
View SolutionTotal number of four digit odd numbers that can be formed by using 0,1,2,3,5,7 is:
View SolutionIf 1+2+3+……………+n=45, then `1^3+2^3+3^3+…………+n^3` is:
View SolutionIf p be the length of the perpendicular from the origin on the line `x/a+y/b=1`, then
View SolutionIf the circles `x^2+y^2=9` and `x^2+y^2+8y+c=0` touch each other, then c is equal to:
View SolutionIf `f(x)=(x-4)/(2sqrt3)`, then f'(1) is equal to?
View SolutionIf A and B are two events, the probability that exactly one of them occurs is given by
View SolutionProve that: `cos20^@+cos100^@+cos140^@=0`.
View SolutionIf `tan3A=(3 tan A+k tan^(3)A)/(1-3 tan^(2)A)`, then k is equal to
View SolutionEvaluate: `[i^20+(1/i)^26]^3`.
View SolutionUsing Binomial theorem prove that:`(1.1)^10000> 10000`
View SolutionWrite the general term in the expansion of `(x^(2)-yx)^(12), x ne 0`
View SolutionLet (4, 2), B (6, 5) and C (1, 4) be the vertices of `triangleABC`. :- The median from A meets BC at D. Find the coordinates of the point D.
View SolutionVerify by the method of contradiction that `sqrt7` is irrational.
View SolutionFind the component statement of the following and check whether they are true or not.
A square is a quadrilateral and its four sides are equal.
View SolutionAssume that P(A) = P(B). Show that A = B
View SolutionIf `AxxB={(a,x),(a,y),(b,x),(b,y)}`. Find A and B
View SolutionProve that :
`sin (A + B) sin (A - B) = sin^2A- sin^2B`.
View SolutionUsing principle of mathematical induction, prove that:
`1/1.2.3+1/2.3.4+1/3.4.5+………….+1/(n(n+1)(n+2))=(n(n+3)/(4(n+1)(n+2))` for all `n in N`.
View SolutionDetermine the number of ways of choosing 5 cards out of a deck of 52 cards which include at least one king.
View SolutionA question paper has two parts: Part A and Part B. each part containing ten questions. If the student has to choose 8 questions form part A and 5 questions from part B. In how many ways can he choose the questions?
View SolutionA.M. between two numbers is 10 and their G.M is 8. Find the numbers.
View SolutionThe sum of first four terms of an A.P is 56. the sum of last four terms is 112. If the first term is 11. find the number of terms.
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that `(1)/(p^(2)) = (1)/(a^(2)) +(1)/(b^(2))`.
View SolutionFind the equation of ellipse with major axis along x-axis passes through the points (4,3) and (-1,4).
View SolutionEvaluate:
`underset(xrarr0)lim (3sinx-sin3x)/x^3`
View SolutionFind the derivative of the funciton `f(x)=2x^2+3x-5` at x=-1. also prove that `f'(0)+3f'(-1)=0`.
View SolutionState wheter is trure or false : If E and F are mutually exclusive events then P `P(E uu F) = P(E) + P(F)`
View SolutionIf z=x+iy and |z+6|=|2z+3|. Then show that `x^2+y^2=9`.
View SolutionIf z= x + iy, x, y real, prove that : `|x|+|y| le sqrt2 |z|`.
View SolutionSolve the inequalities given below for real x :- `1/2((3x)/5+4) ge 1/3 (x-6)`
View SolutionTo receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
View SolutionEvaluate:`underset(xrarra)lim [(x+2)^(3/2)-(a+2)^(3/2)]/(x-a)`.
View SolutionIf `y=sqrtx+1/(sqrtx)`, then show that `2x(dy)/(dx)`+y = 2√ x
View SolutionFind the mean deviation from median of the data:
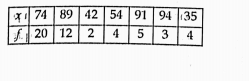
View SolutionFind the mean deviation from the mean for the following data:

View Solution
EXERCISE questions and complete solutions for chapter MODEL PAPER (11) of JBD PUBLICATION of Class 11