Complete Solutions to EXERCISE of chapter MODEL PAPER (15) of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MODEL PAPER (15) |
| JBD PUBLICATION | EXERCISE |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
What is the set builder form of the set {1,2,3}.
View SolutionThe range of the function `f(x)=(x+2)/|x+2|`, `xne-2` is:
View SolutionThe solutions of the equation `sin^2x+3sinx=0` is:
View SolutionThe value of `(2+sqrt(3))(2-sqrt(3))` is:
View Solution`nC_r+^nC_(r+1)=^(n+1)C_x`, then x is equal to:
View SolutionThe nth term of a G.P. is 128 and the sum of its n terms is 225. If its common ratio is 2, then its first term is:
View SolutionThe three striaght lines ax+by=c, bx+cy=a and cx+ay=b are collinear if:
View SolutionIf the circle `x^2+y^2+2ax+8y+16=0` touches x axis, then the vlaue of a is:
View SolutionIn a single toss of three coins, the probability of getting head and tail alternatively is:
View SolutionProve that:`(sinx +sin3x)/(cosx+cos3x)=tan2x`
View SolutionProve that `(sin(x+y))/(sin(x-y))=(tanx+tany)/(tanx-tany)`
View SolutionIf `z_1= 2 -i, z_2= 1+ i`, find `|(z_1+z_2+1)/(z_1-z_2+1)|`.
View SolutionShow that `9^(n+1) - 8n -9` is divisible by 64, whenever n is a positive integer.
View SolutionCompute `(98)^5`
View SolutionUsing distance formula, show that the points A(6,-7,1), B(2,-3,1) and C(4,-5,0) are collinear.
View SolutionShow that the statement is true by the method of contradiction. If x is an integer and `x^2` is even, then x is also even.
View SolutionFind the component statement of the following and check whether they are true or not.
24 is a multiple of 2,4 and 8.
View SolutionProve that `A^c-B^c=B-A`.
View SolutionIf `f(x)=log(x/(x-1))`, show that `f(x+1)+f(x)=log ((x+1)/(x-1))`
View SolutionProve that:`cos15^@-sin15^@=1/sqrt2`
View SolutionProve that : `cos 24^@+ cos 55^@ + cos 125^@ + cos204^@ + cos 300^@= 1/2`.
View SolutionHow many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER ?
View SolutionFind the value of n such that :
`"^nP_5=42 ^nP_3, n>4`.
View SolutionSum of first p,q and r terms of an A.P. are a,b,c respectively. Prove that `a/p(q-r) +b/q(r-p) + c/r(p-q)=0`.
View SolutionIf the angle between two lines is `pi/3` and slope of one of the line is `1/4`. Find the slope of other line.
View SolutionIf a parabolic reflector is 20 cm in diameter and 50 cm deep. Find the focus.
View SolutionEvaluate: `underset(xrarr1)lim ((x+x^2+x^3+……….x^n)-n)/(x-1)`
View SolutionIf y=asinx+bcosx, prove that`y^2+((dy)/(dx))^2=a^2+b^2`
View SolutionA,B and C are three mutually exclusive and exhaustive events associated with a random experiment . Find P(A) given that `P(B)=(3)/(2)P(A)andP(C )=(1)/(2)P(B)`.
View SolutionFind `theta` such that `(3+2i sin theta)/(1-2i sin theta)` is purely real.
View SolutionIf `a + ib = ((x+i)^2)/(2x^2+1)`, prove that `a^2+b^2 =((x^2+1)^2)/((2x^2+1)^2)`.
View SolutionSolve the following system of inequalities graphically: `4x + 3y le 60, y ge 2x, x ge 3, x, y ge 0`
View SolutionIQ of a person is given by the formula `IQ= (MA)/(CA)xx100` , where MA is mental age and CA is chronological age. If `80 le IQ le 140` for a group of 12 years old children, find the range of their mental age.
View SolutionEvaluate: `underset(xrarr0)lim (sqrt(1+2x)-sqrt(1-2x))/(x)`
View SolutionFind the derivative of cos x w.r.t. x
View SolutionFind the mean marks from the following data :
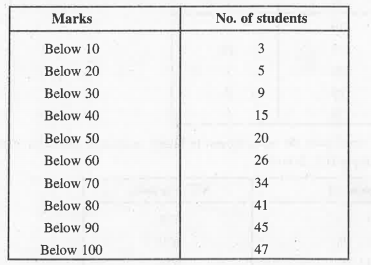
View SolutionFind the mean deviation from the mean for the following data. 38, 70, 48, 40, 42, 55, 63, 46, 54, 44.
View Solution
EXERCISE questions and complete solutions for chapter MODEL PAPER (15) of JBD PUBLICATION of Class 11