Complete Solutions to EXAMPLE of chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | INTRODUCTION TO THREE DIMENSIONAL GEOMETRY |
| JBD PUBLICATION | EXAMPLE |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
Show that the points (-2,3,5), (1,2,3) and (7,0,-1) are collinear.
View SolutionName the octants in which the following point lie:
A(2,3,4), B(5,-3,3),C(2,-1,-6),D(2,2,-3),E(-1,3,-6),F(-1,3,3),G(-3,-2,5) and H(-1,-2,5).
View SolutionFind the distance between the following pairs of points:
(6,-1,5) and (-2,1,3)
View SolutionFind the distance between the following pairs of points
(-1, 3, -4), (1, -3, 4)
View SolutionFind the value of x, so that the point (6,5,-3) is at a distance of 13 units from the point (x,-7,0).
View SolutionFind the coordinates of a point on the z-axis which is equidistant from point A(3,2,1) and B(5,2,5).
View SolutionFind the points on x-axis which are at a distance of `sqrt29` units from point A(1,2,3).
View SolutionIf A and B be the points (3,4,5) and (-1,3,-7) respectively, find the equation of the set of point P such that `PA^2+PB^2=k^2`, where k is constant.
View SolutionShow that if `x^2+y^2=1`, then the point `(x,y,sqrt(1-x^2-y^2))` is at a distance of 1 unit from the origin.
View SolutionFind the coordinates of the centroid of a triangle the mid points of whose sides are (1,2,-3), (3,0,1) and (-1,1,-4)
View SolutionFind the ratio in which the line joining the points (4,8,10) and (6,10,-8) is divided by YZ-plane.
View SolutionGiven that P(3,2,-4), Q(5,4,-6) and R(9,8,-10) are collinear. Find the ratio in which Q divides PR.
View SolutionUsing section formula, prove that the three points (-4,6,10), (2,4,6) and (14,0,-20) are collinear.
Also find the ratio in which point B divides the join of A and C.
View SolutionFind the coordinates of the points which trisect the line segment joining the points P(4,2,-6) and Q(10,-16,6).
View SolutionA point R with x-co-ordinate 4 lies on the line segment joining the points P(2,-3,4) and Q(8,0,10). Find the co-ordinate of the point R.
View SolutionFind the lenghts of the medians of the triangle with vertices A(0,0,6), B(0,4,0) and C(6,0,0)
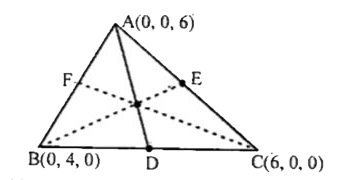
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinats of the point C.
View SolutionIf the origin is the centroid of triangle ABC, with vertices A(a,1,3), B(-2,b,-5) and C(4,7,c). Find the values of a,b and c.
View Solution
EXAMPLE questions and complete solutions for chapter INTRODUCTION TO THREE DIMENSIONAL GEOMETRY of JBD PUBLICATION of Class 11