Complete Solutions to EXERCISE 3.5 of chapter TRIGONOMETRIC FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | TRIGONOMETRIC FUNCTIONS |
| KUMAR PRAKASHAN | EXERCISE 3.5 |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
If any triangle ABC, `a=18,b=24,c=30`
`cosA,cosB,cosC`
View SolutionIf any triangle ABC, `a=18,b=24,c=30`
`sinA,sinB,sinC`
View SolutionFor any triangle ABC, prove that :
`(a+b)/(c)=(cos((A-B)/(2)))/(sin""(C)/(2))`
View SolutionFor any triangle ABC, prove that :
`(a-b)/(c )=(sin((A-B)/(2)))/(cos((C)/(2)))`
View SolutionFor any triangle ABC, prove that :
`sin""(B-C)/(2)=(b-c)/(a)cos((A)/(2))`
View SolutionFor any triangle ABC, prove that :
`a(bcosC-c cosB)=b^(2)-c^(2)`
View SolutionFor any triangle ABC, prove that :
`a(cosC-cosB)=2(b-c)cos^(2)""(A)/(2)`
View SolutionFor any triangle ABC, prove that :
`(sin(B-C))/(sin(B+C))=(b^(2)-c^(2))/(a^(2))`
View SolutionFor any triangle ABC, prove that :
`(b+c)cos((B+C)/(2))=acos((B-C)/(2))`
View SolutionFor any triangle ABC, prove that :
`acosA+bcosB+c cosC=2asinBsinC`
View SolutionFor any triangle ABC, prove that :
`(cosA)/(a)+(cosB)/(b)+(cosC)/(c)=(a^(2)+b^(2)+c^(2))/(2abc)`
View SolutionFor any triangle ABC, prove that :
`(b^(2)-c^(2))cotA+(c^(2)-a^(2))cotB+(a^(2)-b^(2))cotC=0`.
View SolutionFor any triangle ABC, prove that :
`((b^(2)-c^(2))/(a^(2)))sin2A+((c^(2)-a^(2))/(b^(2)))sin2B+((a^(2)-b^(2))/(c^(2)))sin2C=0`
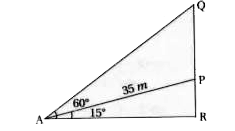
View SolutionA tree stands vertically on a hill side which makes an angle of `15^(@)` with the horizontal. From a point on the ground `35m`. Down the hill from the base of the tree, the angle of elevation of the top of the tree is `60^(@)`. Find the height of the tree.
View SolutionTwo ships leave a port at the same time. One goes 24 km per hour in the direction `N45^(@)E` and other travels `32km` per hour in the directions `S75^(@)E`. Find the distance between the ships at the end of 3 hours.
View SolutionTwo trees A and B are the same side of a river. From point c in the river the distance of the trees A and B is `250mand300m` respectively. If the angle C is `45^(@)`, find the distance between the trees. (Use `sqrt(2)=1.44`)
View Solution
EXERCISE 3.5 questions and complete solutions for chapter TRIGONOMETRIC FUNCTIONS of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS TRIGONOMETRIC FUNCTIONS
- EXERCISE 3.1
- EXERCISE 3.2
- EXERCISE 3.3
- EXERCISE 3.4
- EXERCISE 3.5
- MISCELLANEOUS EXERCISE : 3
- PRACTICE WORK
- QUESTION OF MODULE (KNOWLEDGE TEST)
- SOLUTION OF NCERT EXEMPLAR PROBLEMS (FILLERS)
- SOLUTION OF NCERT EXEMPLAR PROBLEMS (LONG ANSWER TYPE QUESTIONS)
- SOLUTION OF NCERT EXEMPLAR PROBLEMS (OBJECTIVE TYPE QUESTIONS)
- SOLUTION OF NCERT EXEMPLAR PROBLEMS (SHORT ANSWER TYPE QUESTIONS)
- TEXTBOOK BASED MCQS
- TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK