Complete Solutions to Textbook Illustrations for Practice Work of chapter STRAIGHT LINES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | STRAIGHT LINES |
| KUMAR PRAKASHAN | Textbook Illustrations for Practice Work |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Find the slope of the lines :
(a) Passing through the points `(3, -2) and (-1, 4),`
View SolutionFind the slope of the lines :
(b) Passing through the points `(3, - 2) and (7, - 2),`
View SolutionFind the slope of the lines :
(c) Passing through the points `(3, - 2) and (3, 4),`
View SolutionFind the slope of the lines :
(d) Making inclination of 60° with the positive direction of x-axis.
View SolutionIf the angle between two lines is `(pi)/(4)` and slope of one of the lines is `(1)/(2)`, find the slope of the other line.
View SolutionLine through the points `(-2,6) and (4,8)` is perpendicular to the line through the points `(8,12) and (x,24).` Find the value of `x`.
View SolutionThree points `P(h,k), Q(x_(1) , y_(1) ) and R(x_(2) , y_(2) )` lie on a line. Show that, `(h-x_(1) ) (y_(2) -y_(1) ) = (k-y_(1) ) ( x_(2) - x_(1) )`.
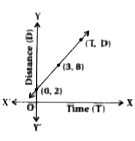
View SolutionIn Figure, time and distance graph of a linear motion is given.
Two positions of time and distance are recorded as, when `T=0, D=2` and when `T=3, D=8`. Using the concept of slope, find law of motion, i.e., how distance depends upon time.
View SolutionFind the equations of the lines parallel to axes and passing through`(-2, 3)`.
View SolutionFind the equation of the line through `(-2,3)` with slope `-4`.
View SolutionWrite the equation of the line through the points `(1,-1) and (3,5)`.
View SolutionWrite the equation of the lines for which `tan theta = (1)/(2),` where `theta` is the
(i) y -intercept is `= -(3)/(2)`
View SolutionWrite the equation of the lines for which `tan theta = (1)/(2),` where `theta` is the
(ii) x intercept is `=4`.
View SolutionFind the equation of the line, which makes intercepts `-3 and 2` on the `x- and y-` axes respectively.
View SolutionFind the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with positive direction of x -axis is 15°.
View SolutionThe fahrenheit temperature F and absolute temperature K satisfy the linear equation. Given that `K = 273` when `F = 32` and that `K = 373` when `F=212`. Express K in terms of `F` also find value of `F` when `K=0`.
View SolutionEquation of a line is `3x-4y+ 10 =0`. Find its
(i) slope,
View SolutionEquation of a line is `3x-4y+ 10 =0`. Find its
(ii) x -intercepts and y -intercepts.
View SolutionReduce the equation `sqrt(3) x + y- 8=0` into normal form. Find the value of `p and omega`.
View SolutionFind the angle between the lines `y- sqrt(3) x - 5 = 0 and sqrt(3) y - x+6=0`.
View SolutionShow that two lines `a_(1) x + b_(14) y + c_(1) = 0 and a_(2) x + b_(2) y + c_(2) = 0`, where `b_(1) , b_(2) ne 0` are
(i) Parallel if `(a_1)/( b_1) = (a_2)/( b_2) and`
View SolutionShow that two lines `a_(1) x + b_(14) y + c_(1) = 0 and a_(2) x + b_(2) y + c_(2) = 0`, where `b_(1) , b_(2) ne 0` are Perpendicular if `a_(1) a_(2) + b_(1) b_(2) =0`.
View SolutionFind the equation of a line perpendicular to the line `x-2y+ 3=0` and passing through the point `(1,-2)`.
View SolutionFind the distance of the point `(3, -5)` from the line `3x - 4y - 26 = 0.`
View SolutionFind the distance between the parallel lines `3x-4y+7=0 and 3x - 4y + 5=0`.
View SolutionFind the equation of line parallel to the Y- axis and drawn through the point of intersection of `x-7+5 = 0 and 3x + y -7=0`.
View SolutionFind the new coordinates of point `(3,-4)` if the origin is shifted to `(1,2)` by a translation.
View SolutionFind the transformed equation of the straight line `2x - 3y + 5 = 0,` when the origin is shifted to the point `(3, -1)` after translation of axes.
View SolutionIf the lines `2x+ y-3 = 0, 5x+ky - 3=0 and 3x -y -2 =0` are concurrent, find the value of k.
View SolutionFind the distance of the line `4x - y = 0 ` from the point P `(4, 1)` measured along the line making an angle of `135^(@) ` with the positive x- axis.
View SolutionAssuming that straight lines work as the plane mirror for a point, find the image of the point `(1,2)` in the line `x - 3y + 4 =0`.
View SolutionShow that the area of the triangle formed by the lines `y= m_(1) x + c_(1) , y= m_(2) x + c_(2) and x = 0` is `((c_1 - c_2)^2)/( 2| m_1 - m_2 | )`.
View SolutionA line is such that its segment between the lines `5x-y + 4=0 and 3x + 4y - 4 =0` is bisected at the point `(1,5)`. Obtain its equation.
View SolutionShow that the path of a moving point such that its distances from two lines `3x - 2y = 5 and 3x + 2y = 5` are equal is a straight line.
View Solution
Textbook Illustrations for Practice Work questions and complete solutions for chapter STRAIGHT LINES of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS STRAIGHT LINES
- Exercise : 10.1
- Exercise : 10.2
- Exercise : 10.3
- Exercise : 10.4
- Exercise : 10.5
- Latest Exam MCQs
- Miscellaneous Exercise : 10
- Practice Work
- Question of Module (Knowledge Test :)
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Matching The Columns)
- Solutions of NCERT Exemplar Problems (Objective type Questions)
- Solutions of NCERT Exemplar Problems (Short Answer Type Questions)
- Text based MCQs
- Textbook Illustrations for Practice Work