Complete Solutions to PRACTICE WORK of chapter PROBABILITY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | PROBABILITY |
| KUMAR PRAKASHAN | PRACTICE WORK |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
Two coins (a one rupee coin and a two rupee coin) are tossed once. Find a sample space.
View Solutiondescribe the sample space for the indicated experiment. From a group of 2 boys and 3 girls, two children are selected.
View SolutionWrite the sample space at an event that coin is tossed till to head is obtained observe that it is an example of finite or infinite sample space.
View SolutionSuppose 3 bulbs are selected at random from a lot. Each bulb is tested and classified as defective (D) or non-defective (N). Write the sample space of this experiment.
View SolutionAn experiment consists of rolling a die and then tossing a coin once if the number on die is even. If the number on die is odd, the coin is tossed twice. Write the sample space for this experiment.
View SolutionA coin is tossed thrice. If all the three times, the result is tail, a die is thrown. Otherwise the experiment become end. Write the sample space for this experiment.
View SolutionTwo cards are selected randomly from four cards denoted as A, B, C, D without replacement. Describle the sample space for this experiment.
View SolutionA box contain 3 identical red balls, 3 identical white balls and 1 black ball. A ball is selected randomly from a bag and then put it in the bag. Aging a ball is drawn. Write the sample space for this experiment.
View SolutionA coin is tossed. If the result is head, a coin is tossed again. If the result is tail, a die is thrown. Write the sample space for this experiment.
View SolutionThree distinct balls are placed in two drawers. Write the sample space for this experiment.
View SolutionA sample space 5 consists 1 to 30 positive integers. Event A Ai shows the elementary divisible by i. Write the elements of the events `A_(2),A_(3),A_(4),A_(5)`. Veify the truthless of following statements.
(1) `A_(2)` and `A_(3)` are mutually exclusive events.
(2) `A_(4)` is a subset of `A_(2)`.
(3) `A_(3),A_(4)` and `A_(5)` are not mutually exclusive.
View SolutionA die is throw. Describe the following events :
A: The number on die is less than 7.
B: The number on die is multiple of 3.
C : The number on die is greater than 4.
D: The number on die is smaller than 2.
Also find `AnnC,BuuC,D'uuC'`.
View SolutionA bag contains a red ball, a black ball, a yellow ball and a white ball. One ball is selected randomly and note its colour and then put it into the bag. Again second ball is selected and note its colour. Write the sample space for this experiment. Hence, describe the following events :
(1) A: Selected both the balls are of same colours.
(2) B: Only one ball is white.
(3) C: At least one ball is white.
(4) D: Both the balls are of different colour.
Hence, find `AnnB,BuuC,AuuD,AnnD`. What can we say about the events B and C ? What can we say about the events A and D?
View SolutionTwo dice are thrown write the sample space for this experiment. Describe the following events.
Event A : The sum of the number on the dice is divisible by 4.
Event B : The sum of the numbers on the dice is divisible by 3.
Event C: The sum of the numbers is less than 7.
Event D: Both the numbers on the dice are even.
View SolutionThree dice are rolling simultaneously. Find the probability of getting same numbers on all dice.
View SolutionThe integer is selected at random from 1 to 25. The probability that it is a prime number is
View SolutionAn urn contains 7 white, 5 black and 3 read balls. Two balls are drawn at random. Find the probability that.
(i) Both the balls are red.
(ii) One balls is red and other is black.
One ball is white.
View SolutionA single letter is selected at random from the word 'PROBABILITY'. The probability that it is a vowel is
View SolutionA card is drawn at random from pack of 52 playing cards. Find the probability of getting (i) a face card (ii) red card.
View SolutionA five digit number is formed by the digits 1, 2, 3, 4, 5 without repetition. Find the probability that the number is divisible by 4.
View SolutionThree squares of chess board are selected at random. Find the probability of getting 2 squares of one colour and other of a different colour.
View SolutionWhat is the probability that in a leap year chosen at random will contain 53 Sunday?
View SolutionA and B are mutually exclusive event. If `P(A)=(1)/(4),P(B)=(2)/(5)` and `P(AuuB)=(1)/(2)`.
View SolutionA die is thrown twice. What is the probability that at least one of the two throws comes up with the number 4 ?
View SolutionA, B and C are mutually exclusive and exhaustive events. If `P(B)=(3)/(2)P(A) and P(C)=(1)/(2)P(B),` then find P(A).
View SolutionFollowing Vann diagram show the probabilities of three events.
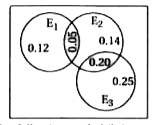
Find the following probabilities.
(i) `P(E_(2))` (ii) `P(E_(2)nnE_(3))`
(iii) `P(E_(1)uuE_(2))` (iv) `P(E_(1)nnE_(2)')`
View SolutionFind the probability of getting almost two tails or at least two heads in a toss of three coins.
View SolutionA number is chosen at random from the numbers 20 to 50. What is the probability that the number chosen is a multiple of 3 or 5 or 7 ?
View SolutionA basket contains 15 guava and 12 banana. Out of which 5 guava and 7 banana are defective. If a person takes out 3 at random, then what is the probability that either all are guava or all are good?
View SolutionIf A and B are mutually exclusive events, `P(A) = 0.35` and `P(B)= 0.45`, find
(i)` P(A')` (ii) `P(B')` (iii) `P(AcupB)`
(iv) `P(AcapB)` (v) `P(AcapB')` (vi) `P(A'capB')`
View SolutionFind the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards it contains :
(i) All queens
(ii) 3 Queens
(iii) At least 3 Queens
View SolutionIn an interview for a job, 5 boys and 3 girls appeared. If 4 persons are to be selected at randon from this group, then find the probability that 3 boys and 1 girl or 1 boy and 3 girls are selected.
View SolutionA box contains 8 red, 3 white and 9 black balls. If three balls are drawn at random, find the probability that:
(i) All three balls are of different colour,
(ii) One ball is red and two balls are white.
(iii) All three balls are black.
View SolutionA group consists of 3 men, 2 women and 4 children. If four persons are selected at| random, find the probability of selecting :
(i) 1 man, 1 woman and 2 children
(ii) Exactly 2 children (iii) 2 women
View SolutionAn integer is chosen at random from first 200 natural numbers. What is the probability that the integer chosen is divisible by 6 or 8 ?
View SolutionThe probability that a student will receive A, B, C or D grade are 0.40, 0.50, 0.15 and 0.10 respectively. Find the probability that a student will receive (i) B or C grade (ii) At least C grade.
View SolutionA and B are mutually exclusive events. P(A)=0.28, P(B)=0.38, then find (i) `P(AuuB)`, (ii) `P(AnnB),` (iii) `P(AnnB')`, (iv) `P(A'nnB')`
View SolutionWithout repetition of the numbers, four digit numbers are formed with the numbers 0, 2, 3, 5. The probability of such a number divisibele by 5 is
View SolutionThree of six vertices of a regular hexagon are chosen at random. What is the probability that the triangle with these vertices is equilateral ?
View SolutionTwo dice are thrown together. What is the probability that sum of the numbers on the two faces is neither divisible by 3 not by 4 ?
View Solution
PRACTICE WORK questions and complete solutions for chapter PROBABILITY of KUMAR PRAKASHAN KENDRA MATHS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 MATHS PROBABILITY
- EXERCISE : 16.1
- EXERCISE : 16.2
- EXERCISE : 16.3
- Miscllaneous Exercise : 16
- PRACTICE WORK
- Question of Module
- Solutions of NCERT Exemplar Problems (Fillers)
- Solutions of NCERT Exemplar Problems (Long Answer Type Questions)
- Solutions of NCERT Exemplar Problems (Match the followings
- Solutions of NCERT Exemplar Problems (Objective type Questions)
- Solutions of NCERT Exemplar Problems (Short Answer Type Questions)
- Solutions of NCERT Exemplar Problems (True/False)
- Textbook based MCQs
- Textbook Illustrations for Practice Work