Complete Solutions to SECTION-B NUMERICALS of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| KUMAR PRAKASHAN | SECTION-B NUMERICALS |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g, and 200g respectively. Each side of the equilateral triangle is 0.5m long.
View SolutionFind the centre of mass of a triangular lamina.
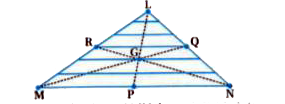
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the scalar and vector products of two vectors. `a = (3hati – 4hatj + 5hatk) and b = (– 2hati + hatj – 3hatk )`
View SolutionFind the torque of a force `7hati + 3hatj – 5hatk` about the origin. The force acts on a particle whose position vector is `hati – hatj + hatk`.
View SolutionShow that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
View SolutionShow that moment of a couple does not depend on the point about which you take the moments.

View SolutionA metal bar 70 cm long and 4.00 kg in mass supported on two knife-edges placed 10 cm from each end. A 6.00 kg load is suspened at 30 cm from one end. Find the reactions at the knife-edges. (Assumes the bar to be of uniform cross section and homogeneous).

View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.
View SolutionWhat is the moment of inertia of a disc about one of its diameter?
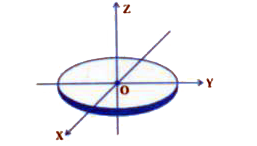
View SolutionWhat is the moment of inertia of a rod of mass M, length l about an axis perpendicular to it through one end?
View SolutionWhat is the moment of inertia of a ring about a tangent to the circle of the ring?
View SolutionObtain equation `omega=omega_(0)+alphat` from first principle.
View SolutionThe angular speed of a motor wheel is increased from 1200 rpm to 3120 rpm in 16 seconds. (i) What is its angular acceleration, assuming the acceleration to be uniform? (ii) How many revolutions does the engine make during this time?
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
View SolutionThree bodies, a ring, a solid cylinder and a solid sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity?
View SolutionIn `DeltaABC`, mass of 100g, located on point A, mass of 200 g located on point C and mass of 150 g is located at point B, they are kept in xy-plane, find the coordinate of centre of mass of `DeltaABC`.
View SolutionFind the centre of mass of uniform thin sheet as shown in figure.

View SolutionFind the centre of mass of uniform thin sheet as shown in figure.

View SolutionIf `veca=2hati-hatj-5hatk and vecb=hati+hatj+2hatk`, then find scalar and vector product.
View SolutionIf a position vector of a point is `vecr=7hati+3hatj+hatk` and force acting on it is `vecF=-3hati+hatj+5hatk` then find torque.
View SolutionProve that moment of inertia of uniform ring of mass M and radius R about its geometric axis is `MR^(2)`
View SolutionFind the moment of inertia and radius of gyration of uniform cross-section rod of mass 4 kg and length 90 cm about an axis through one end and perpendicular to the length of rod.
View SolutionFind the moment of inertia and radius of gyration of uniform cross-section rod of mass M and length l about an axis through a point at distance `(l)/(3)` from one end and perpendicular to the length of rod.
View SolutionFind moment of inertia of a ring of mass 4kg and radius 20cm about its tangent.
View SolutionInitial angular speed of wheel is 20 rad `s^(-1)`. Its angular displacement during 10 s is 100 rad then how many revolution it makes from initially to remain rest. What is its angular acceleration?
View SolutionThe angular speed of a motor wheel is increased from 600 rpm to 1560 rpm in 8 seconds. (i) What is its angular acceleration, assuming the acceleration to be uniform? (ii) How many revolutions does the engine make during this time?
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
View SolutionThree bodies, a ring, a solid cylinder and a solid sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity?
View Solution
SECTION-B NUMERICALS questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- SECTION-A (TRY YOURSELF (VSQs))
- SECTION-A HOTS
- SECTION-A QUESTIONS - ANSWERS
- SECTION-B ADDITIONAL EXERCISE
- SECTION-B NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK
- SECTION-B NUMERICALS
- SECTION-B NUMERICALS FROM TEXTUAL EXERCISE
- SECTION-C OBJECTIVE QUESTIONS (VSQs)
- SECTION-D NCERT EXEMPLAR SOLUTIONS
- SECTION-D NCERT EXEMPLAR SOLUTIONS (LONG ANSWER TYPE QUESTIONS)
- SECTION-D NCERT EXEMPLAR SOLUTIONS (SHORT ANSWER TYPE QUESTIONS)
- SECTION-D NCERT EXEMPLAR SOLUTIONS (VERY SHORT ANSWER TYPE QUESTIONS)
- SECTION-E MULTIPLE CHOICE QUESTIONS
- SECTION-F (SECTION-A) QUESTIONS PAPER
- SECTION-F (SECTION-B) QUESTIONS PAPER
- SECTION-F (SECTION-C) QUESTIONS PAPER
- SECTION-F (SECTION-D) QUESTIONS PAPER
- SECTION-F QUESTIONS FROM MODULE