Complete Solutions to SECTION - B Numerical From DARPAN Based On Textbook of chapter MECHANICAL PROPERTIES OF FLUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICAL PROPERTIES OF FLUIDS |
| KUMAR PRAKASHAN | SECTION - B Numerical From DARPAN Based On Textbook |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
It is known that density `rho` of air decreases with height y as
`-y//y_(0)`
`rho=rho_(o)e`
where `rho_(o)=1.25kgm^(-3)` is the density at sea level and `y_(o)` is a constant . This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions).Also assume that the value of g remains constant.
(b) A large He balloon of volume `1425m^(3)` is used to lift a payload of 400 kg . Assume that the balloon maintains constant radius as it rises . How high does it rise ? `(y_(o)=8000mandrho_(He)=0.18kgm^(-3))`.
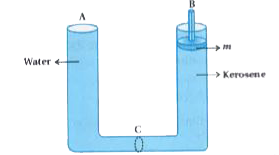
View SolutionAs shown in the figure two cylindrical vessels A and B are interconnected . Vessel A contains water up to 2m height and vessel B contains kerosene . Liquids are separated by movable, airtight disc C . If height of kerosene is to be maintained at 2m , calculate the mass to be placed on the piston kept in vessel B. Also calulate the force acting on disc C due to this mass. Area of piston `=100cm^(2)`, area of disc
`C=10cm^(2)` , Density of water `=10^(3)kgm^(-3)`, specific density of kerosene `=0.8`.
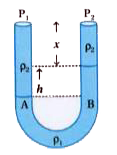
View SolutionAs shown in figure lower portion of the manometer tube contains fluid of density `rho_(1)` and the upper part contains fluid of density `rho_(2)(rho_(1)gtrho_(2))` .
If pressures on the top of these two arms are `P_(1)andP_(2)`, calculate pressure differnce `(P_(1)-P_(2))`.
View SolutionThe diameter of one end of a tube is 2 cm and that of another end is 3 cm . Velocity and pressure of water at narrow end are `2ms^(-1)and1.5xx10^(5)Nm^(9-2)` respectively . If the height differnce between narrow and broad ends is 2.5 m , find the velocity and pressure of water at the broad end .(Density of water is `1xx10^(3)kgm^(-3))`. The narrow end is higher .
View SolutionWater is filled in a container upto height H as shown in the figure . A small hole is board on the surface of a container at the depth h from the surface of water . What will be the distance of a point along the horizontal where the jet of the water strikes the ground ? For which value of h will this distance be maximum ? Also find this maximum distance.

View SolutionThe velocities of cylindrical layers of liquid flowing through a tube , situated at distances `0.8cm and 0.82cm` from the axis of the tube are `3cms^(-1)and2.5cms^(-1)` respectively . Find the viscous force acting between these layers , if the length of the tube is 10 cm and the coefficient of viscosity of the liquid is 8 poise .
View SolutionTwo rain drops of equal volume , falling with terminal velocity `10cms^(-1)` , merge while falling and forms a larger drop . Find the terminal velocity of the larger drop .
View SolutionThe radius of a pipe decreases according to `r=r_(o)e^(-propx)` , where `alpha=0.50m^(-1)andx` is the distance of a cross - section from the first end (x=0) . Find the ratio of Reynolds number for two cross -sections lying at the distance of 2m from each other . (take `e=2.718)`
View SolutionFind the pressure in a bubble of radius 0.2 cm formed at the depth of 5cm from the free surface of water . The surface tension of water is 70 dyne `cm^(-1)` and its density is `1gcm^(-3)` . Atmospheric pressure is `10^(6)` dyne `cm^(-2)` .The gravitational acceleration is `980cms^(-2)`.
View SolutionRadius of a glass capillary is 0.5 mm . Find the height of the column of water when it is held vertical in water . The density of water is `10^(3)kg`
`m^(-3)` and the the angle of contact between glass and water is `0^(@),g=9.8ms^(-2)` and the surface tension of water `T=0.0727Nm^(-1)`.
View SolutionThe piston and nozzle of a syringe kept horizontal have diameters 5 mm and 1 mm. the piston is pushed with constant velocity of` 0.2ms^(-2)` Find the horizontal distance travelled by water jet before touchig water`[g=10m//s^(2)]`. Height of syringe from ground is 1 m.
View SolutionWater is flowing through a horizontal pipe of irregular cross section . If the pressure at a point where the velocity is `0.2ms^(-1)` is 30 mm Hg , what will be the pressure at a point where the velocity is `1.2ms^(-1)` ? (Density of mercury `=13.6gcm^(-3),g=1000cms^(-2)` , Density of water `=1gcm^(-3))`
View SolutionFind the work required to be done to increase the volume of a bubble of soap solution having a radius 1mm to 8 times . (surface tension of soap solution is 30 dyne `cm^(-1))`
View SolutionDiameters of the arms of a U tube are 10 mm and 1 mm . It is partially filled with water and it is held in a vertical plane . Find the difference in heights of water in both the arms . (Surface tension of water =70 dyne `cm^(-1)` angle of contact `=0^(@).g=980cms^(-2))`
View SolutionA bubble of air of diameter 0.2 cm rises up uniformly in water with a velocity of `200cm//s` . If the density of water is `1gcm^(-3)` , find coefficient of viscosity of water. Neglect density of air w.r.t that of water.`(g=9.8m//s^(2))`
View SolutionThe velocity of a cylindrical layer of liquid at a distance 0.4 cm from the axis of a tube of radius 0.5 cm is `3.6cm//s` .Find the velocity of a layer lying at a distance of 0.3 cm from axis .
[Hint : `v=(P)/(4etal)(r^(2)-x^(2))]`
View SolutionWhat should be the difference in pressure across the ends of a 4 km long horizontal pipe line of diameter 8 cm to make water flow at the rate 20 litre/s`eta_("water")=10^(-2)MKS`. Neglect all forces other than viscous force.
[Hint : `V=(piPr^(4))/(8hl)]`
View Solution
SECTION - B Numerical From DARPAN Based On Textbook questions and complete solutions for chapter MECHANICAL PROPERTIES OF FLUIDS of KUMAR PRAKASHAN KENDRA PHYSICS (GUJRATI ENGLISH) of Class 11
All Exercises from KUMAR PRAKASHAN Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS
- QUESTION PAPER (SECTION -A)
- QUESTION PAPER (SECTION -B)
- QUESTION PAPER (SECTION -C)
- SECTION - (D NCERT Exemplar Solution)
- SECTION - (D NCERT Exemplar Solution) (Long Answer Type Questions
- SECTION - (D NCERT Exemplar Solution) (Short Answer Type Questions
- SECTION - (D NCERT Exemplar Solution) (Very Short Answer Type Questions
- SECTION - B Numerical From DARPAN Based On Textbook
- SECTION - B Numerical From Textual Exercise
- SECTION - B Numericals
- SECTION - E (MCQS)
- SECTION - F (Questions from Module)
- SECTION -C (Objective Questions) (VSQs)
- SECTION -C (Objective Questions) (VSQs) Assertion and Reason Type Questions
- SECTION -C (Objective Questions) (VSQs) Fill in the Blank
- SECTION -C (Objective Questions) (VSQs) Match Type Questions
- SECTION-A
- SECTION-A Try Yourself (VSQs)