Complete Solutions to EXAMPLE of chapter MODEL PAPER 18 of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MODEL PAPER 18 |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 44 |
| Academic Year | 2023-24 |
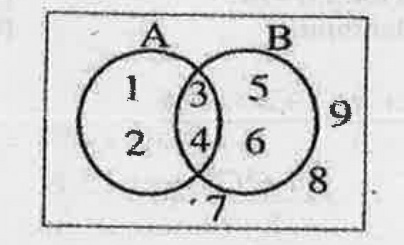
Consider the Venn diagram given below:
Write `A',B',(AbigcapB)'`
 .
.
View SolutionFor any triangle ABC, prove that `sin((B-C)/2)=(b-c)/acos(A/2)`
View SolutionConsider the complex number `z=3+4i`. Write the conjugate of z.
View SolutionConsider the complex number `z=3+4i`.Verify that `zoverlinez=absz^2`
View SolutionSolve the inequality `-5le((5-3x)/2)le8`.
View Solution`-5le((5-3x)/2)le8`.Represent the solution on a number line.
View Solution4 cards are drawn from a well shuffled pack of 52 cards.In how many ways can this be done?
View Solution4 cards are drawn from a well shuffled pack of 52 cards. In how many ways can this be done if all 4 cards are of the same colour?
View SolutionConsider the equation of the ellipse `9x^2+4y^2=36`. Find focci.
View SolutionConsider the equation of the ellipse `9x^2+4y^2=36`. Find Eccentricity.
View SolutionConsider the equation of the ellipse `9x^2+4y^2=36`. find Length of latus rectum.
View SolutionEvaluate `lim_(x→ -4)(2x+8)/(x^2+x-12)`.
View SolutionConsider the statement `P(n):1/1.2+1/2.3+1/3.4+.....+1/{n(n+1)}=n/(n+1)`.Show that P(1) is true.
View SolutionConsider the statement `P(n):1/1.2+1/2.3+1/3.4+.....+1/{n(n+1)}=n/(n+1)`.Prove that P(n) is true for all `n in N` using the principle of mathematical induction.
View SolutionConsider the complex number `z=(1+3i)/(1-2i)`. Write z in the form `a+ib`
View SolutionConsider the complex number `z=(1+3i)/(1-2i)`.Write z in polar form.
View SolutionSolve the following inequalities graphically
`x-2yle3`,`3x+4yge12`,`xge0`,`yge1`
View SolutionHow many 3 letter words with or without meaning can be formed using 26 letters in English alphabet, if no letter is repeated?
View SolutionFind the number of permutation of letters of the word MATHEMATICS.
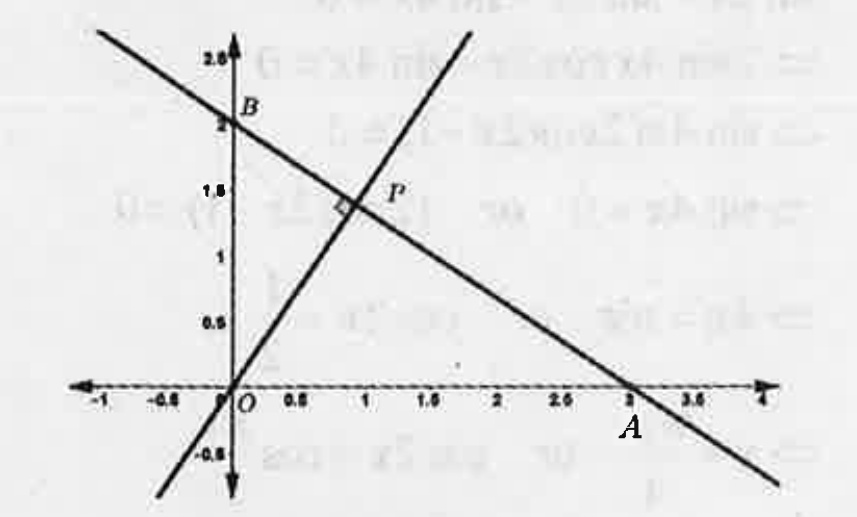
View SolutionConsider the given below. `A(3,0)` and B(0,2)` are two points on axes. The line is perpendicular to AB.
Find the coordinate of the point P.
 .
.
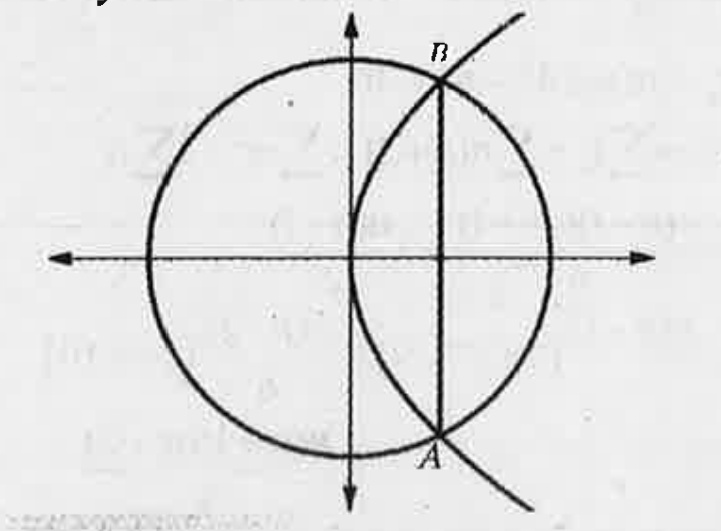
View SolutionEquation of the parabola given in the figure is `y^2=8x`
Find the focus and length of latus rectum of the parabola.
 .
.
View SolutionLet L be the line `x-2y+3=0`.Find the equation of the `L_1` which is parallel to L and passing through (1,-2).
View SolutionLet L be the line `x-2y+3=0`.The equation of line `L_1` is parallel to L and passing through (1,-2).Find the distance between L and `L_1`.
View SolutionConsider a point A (3,2,-1) in space.Write the octant in which A belongs to.
View SolutionConsider a point A (3,2,-1) in space.If B (1,2,3) is another point in space, find the distance between A and B.
View SolutionWrite the contrapositive of the statement.p: If a triangle is equilateral, then it is isosceles.
View SolutionVerify by method of contradiction:
'`sqrt3` is irrational.
View SolutionIf `A={a,b}` write `AtimesAtimesA`.
View SolutionIf `R={(x,x^3):x` is a prime number less than 10}. Write R in roster form.
View SolutionFind the domain and range of the real function `f(x)=2+sqrt(x-1)`
View SolutionThe minute hand of a watch is 3cm long. How far does its tip move in 40 minutes?(use `pi=3.14`)
View SolutionSolve `sin2x-sin4x+sin6x=0`
View SolutionFind the sum of all 3 digit numbers which are multiple of 5.
View SolutionHow many terms of GP `3,3^2,3^3,`..... are needed to give the sum 120?
View SolutionFind the sum of the first n terms of the series whose nth term is `n(n+3)`.
View SolutionExpand using binomial theorem, `(x/3+1/x)^5`.
View SolutionFind `(a+b)^4-(a-b)^4`.
View Solutionevaluate
`(sqrt3+sqrt2)^4-(sqrt3-sqrt2)^4`
View SolutionFind the derivative of `y=1/x` from the first principle.
View SolutionDifferentiate `f(x)=cosx/(1+sinx)` with respect to x.
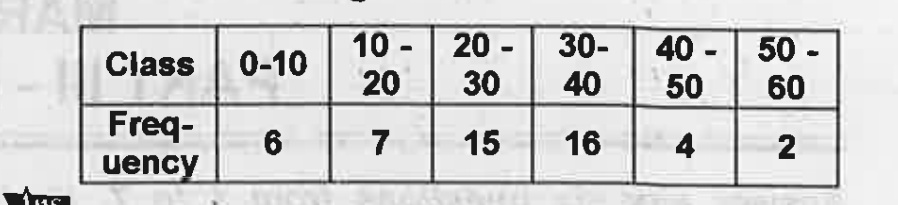
View SolutionCalculate the mean deviation about median for the following data:
 .
.
View SolutionConsider a bag containing 3 red balls and 2 black balls which are identical. 2 balls are drawn simultaneously at random from the bag.Write the sample space of the random experiment.
View SolutionConsider a bag containing 3 red balls and 2 black balls which are identical. 2 balls are drawn simultaneously at random from the bag.
Write the event.
A : Both balls are red.
B : One is red and one is black.
View SolutionConsider a bag containing 3 red balls and 2 black balls which are identical. 2 balls are drawn simultaneously at random from the bag.
A: Both the balls are red
B: One ball is red and another one is black
Show that A and B are mutually exclusive.
View Solution
EXAMPLE questions and complete solutions for chapter MODEL PAPER 18 of MAXIMUM PUBLICATION of Class 11