Complete Solutions to EXAMPLE of chapter QUESTION PAPER MARCH 18 of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | QUESTION PAPER MARCH 18 |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
Find the sum to n terms of the sequence
`4+44+444+…….`
View SolutionSolve: `sin2x-sin4x+sin6x=0`
View SolutionIf A and B are events such that `P(A)=1/4`,`P(B)=1/2`,`P(A nnn B)=1/6`
Then find P(A or B)
View SolutionIf A and B are events such that `P(A)=1/4`,`P(B)=1/2`,`P(A nnn B)=1/6`
Then find P(not A and not B)
View SolutionIn a `/_\ABC` , prove that `tan((B-C)/2)=(b-c)/(b+c)cotfrac(A)(2)`
View SolutionThe maximum value of the function
`f(x)=sinx` is……
View SolutionProve that, `(sinx+cosx)^2=1+sin2x`
View SolutionFind the maximum value of `sinx+cosx`
View Solution`lim_(xrarr2)[x]`=……...
View SolutionEvaluate : `lim_(xrarr2)(x^3-4x^2+4x)/(x^2-4)`
View SolutionOne card is drawn at random from a pack of 52 playing cards. Find the probability that, the card drawn is black.
View SolutionOne card is drawn at random from a pack of 52 playing cards. Find the probability that, the card is face card.
View SolutionOne card is drawn at random from a pack of 52 playing cards. Find the probability that, the card is a black face card.
View SolutionIf `A={a,b,c}`, then write power set of `P(A)`.
View SolutionIf the number of subsets with two elements of a set P is 10,then find the total number of elements in set P.
View SolutionConsider the Venn diagram of the Universal
set `U={1,2,3,4,5,6,7,8,9,10,11,12,13}`
Verify `(A uuu B)'=A' nnn B'`
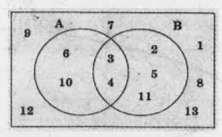
View SolutionConsider the Venn diagram of the Universal
set `U={1,2,3,4,5,6,7,8,9,10,11,12,13}`
Find `n(A nnn B)'`
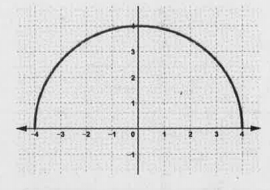
View SolutionThe figure shows the graph of a function `f(x)`
which is a semi circle centered ar origin.
Write the domain and range of `f(x)`
View SolutionIf `3^(2n+2)-8n-9` is divisible by 'k' for all `n in N` is true, then which one of the following is a value of 'k'?a)8 b)6 c)3 d)12
View SolutionProve by using the principal of Mathematical Induction `P(n)=1+3+3^2+…..+3^(n-1)=(3^n-1)/2`is true for all `n in N`
View SolutionSolve the inequality `(2x-1)/3ge(3x-2)/4-(2-x)/5`
View SolutionSolve the inequality `(2x-1)/3ge(3x-2)/4-(2-x)/5`
Represent the solution on a number line.
View SolutionFind the `n^(th)` term of the sequence
3,5,7,………
View SolutionFind the sum to n terms of the series
`3xx1^2+5xx2^2+7xx3^2+`……..
View SolutionFind the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line `4x+y=16`
View SolutionConsider a point `A(4,8,10)` in space
Find the distance of the point A from XY-Plane.
View SolutionConsider a point `A(4,8,10)` in space
Find the distance of the point A from X-axis.
View SolutionConsider a point `A(4,8,10)` in space.Find the ratio in which the line segment joining the point A and B `(6,10,-8)` is divided by YZ-plane.
View SolutionWhich one of the following sentences is a statement? A) 275 is a perfect square. B)Mathematics is a difficult subject C)Answer this question D)Today is a rainy day
View SolutionVerify by method of contradiction `p:sqrt2` is irrational.
View SolutionConsider the quadratic equation
`x^2+x+1=0`
Solve the quadratic equation.
View SolutionConsider the quadratic equation `x^2+x+1=0`.Write the polar form of one of the roots.
View SolutionConsider the quadratic equation `x^2+x+1=0`.If the two roots of the given quadratic are `alpha` and `beta`.Show that `alpha^2=beta`
View SolutionWhich of the following has its middle term independent of x?
View SolutionWrite the expansion of `(x^2+3/x)^4`
View SolutionDetermine whether the expansion of `(x^2+2/x)^18` will contain a term containing `x^10`
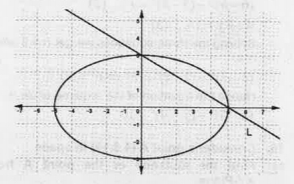
View SolutionThe figure shows an ellipse `x^2/25+y^2/9=1`
and a line L.
Find the equation of the line parallel to the line L and passing through any one of the foci.
View SolutionFind the derivative of `y=sinx` from the first principle.
View SolutionFind `dy/dx`, if `y=(x^5-cosx)/sinx`
View SolutionFind n,if `12times^((n-1))P_3=5times^((n+1))P_3`
View SolutionIf 'nPr'=840,nCr=35 , find r.
View SolutionEnglish alphabet has 5 vowels and 21 consonants. How many 4 letter words with two different vowels and two different consonants can be formed without repetition of letters?
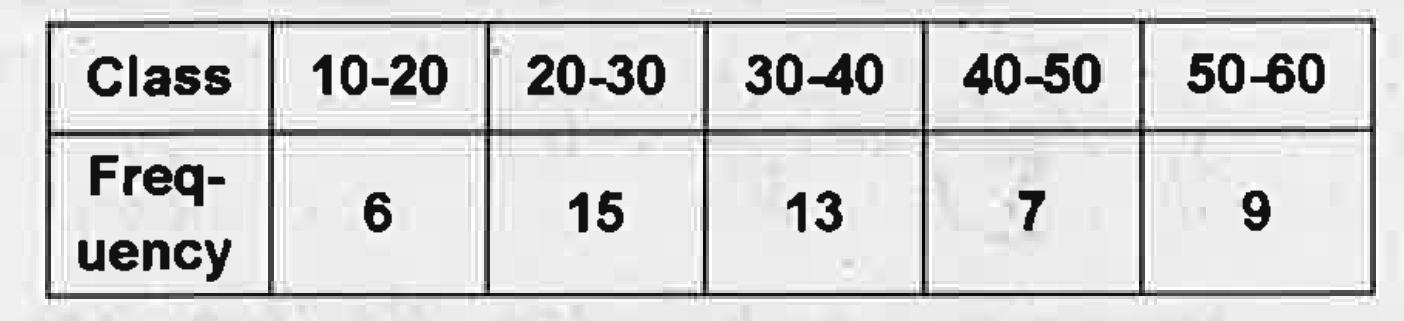
View SolutionConsider the following distribution:
Calculate the mean of the distribution
View SolutionConsider the following distribution,
Find the standard deviation of the distribution.
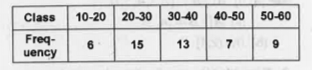
View SolutionConsider the following distribution,
Find the coefficient of variation of the distribution.
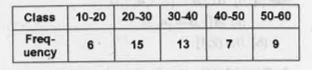
View Solution
EXAMPLE questions and complete solutions for chapter QUESTION PAPER MARCH 18 of MAXIMUM PUBLICATION of Class 11