Complete Solutions to EXAMPLE of chapter Relations and Functions of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | Relations and Functions |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If `(x+1,y-2)=(3,1)` , find the values of x
and y.
View SolutionIf `(x/3+1,y-2/3)=(5/3,1/3)`, find the values
of x and y.
View SolutionIf `G={7,8}`,`H={2,4,5}`,find `GxxH` and `HxxG`.
View SolutionIf `A={-1,1}` find `AxxAxxA`
View SolutionWrite the relation `R={(x,x^3): x` is a prime
number less than 10} in roster form.
View SolutionIf `f(x)=x^2`, find `(f(1.1)-f(1))/((1.1-1))`
View SolutionLet `f={(x,x^2/(1+x^2)),x in R}` be a real
function from R to R. Determine the domain
and range of f.
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=abs[x-2]`
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=x^2`
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=x^3`
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=1/x`
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=(x-1)^2`
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=3x^2-1`
View SolutionGraph the following real functions.
(each carries 2 scores)
`f(x)=abs[x]-2`
View SolutionConsider the relation,
`R={(x,2x-1)//x in A}` where `A={2,-1,3}`
Write R in roster form.
View SolutionConsider the relation,
`R={(x,2x-1)//x in A}` where `A={2,-1,3}`
Write the range of R.
View SolutionLet `A={1,2,3,4,6}` and R be a relation on A
defined by `R={(a,b): a,b in A, b` is exactly
divisible by a}
Write R in the roster form.
View SolutionLet `A={1,2,3,4,6}` and R be a relation on A
defined by `R={(a,b): a, b in A, b` is exactly
divisible by a}
Find the domain and range of R.
View SolutionConsider the real function
`f(x)=(x^2+2x+3)/(x^2-8x+12)`
Find the value of x if `f(x)=1`
View SolutionConsider the real function
`f(x)=(x^2+2x+3)/(x^2-8x+12)`
Find the domain of f.
View SolutionIf `f(x)=x^3+5x` and `g(x)=2x+1`,find
`(f+g)(2)` and `(fg)(1)`.
View SolutionLet `A={1,2,3,4,5}` and R be a relation on A
defined by `R={(a,b):b=a^2}`
Write R in the roster form.
View SolutionLet `A={1,2,3,4,5}` and R be a relation on A
defined by `R={(a,b):b=a^2}`
Find the range of R.
View SolutionDraw the graph of the function
`f(x)=abs[x]+1`,`x in R`
View SolutionDraw the graph of the function
`f(x)=x^2`,`x in R`
View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Write R in roster form.
View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Find the domain of R.
View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Find the range of R.
View SolutionDetermine the domain and range of the
relation R defined by
`R={(x,x+5): x in {0,1,2,3,4,5}}`
View SolutionA function f is defined as `f(x)=2x-5`.
Write down the values of `f(0)`,`f(7)`,`f(-3)`.
View SolutionFind the range of the following functions.
`f(x)=2-3x`,`x in R`,`x>0`
View SolutionFind the range of the following functions.
`f(x)=x^2+2`,x is a real number.
View SolutionFind the range of the following functions.
`f(x)=x`,x is a real number.
View SolutionLet `A={1,2}`,`B={1,2,3,4}`,`C={5,6}` and
`D={5,6,7,8}`.Verify that
`Axx(BnnnC)=(AxxB)nnn(AxxC)`
View SolutionLet `A={1,2}`,`B={1,2,3,4}`,`C={5,6}` and
`D={5,6,7,8}`.Verify that
`AxxC` is a subset of `BxxD`
View SolutionThe arrow diagram given below shows a
relation R from P to Q. Write the relation in
roster form,set-builder form. Find its
domain and range.
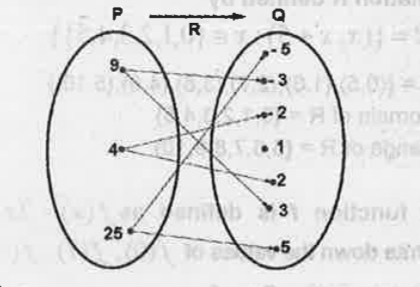
View SolutionFind the domain of the following.
`f(x)=(x^2+2x+1)/(x^2-8x+12)`
View SolutionFind the domain of the following.
`f(x)=(x^2+3x+5)/(x^2-5x+4)`
View SolutionLet `f(x)=sqrtx` and `g(x)=x` be two
functions defined over the set of non-
negative real numbers. Find `(f+g)(x)`, `(f-g)(x)`,`(fg)(x)` and `(f/g)(x)`
View SolutionLet `f(x)=x^2` and `g(x)=2x+1` be two
functions defined over the set of non-
negative real numbers. Find `(f+g)(x)`, `(f-g)(x)`,`(fg)(x)` and `(f/g)(x)`
View Solution`A={1,2}`,`B={3,4}`
Write `AxxB`
View Solution`A={1,2}`,`B={3,4}`
Write relation from A to B in roster form.
View Solution`A={1,2}`,`B={3,4}`
Represent all possible functions from A to B(Arrow diagram may be used)
View SolutionLet `A={1,2,3}`,`B={3,4}` and `C={4,5,6}`.
Find
`Axx(BnnnC)`
View SolutionLet `A={1,2,3}`,`B={3,4}` and `C={4,5,6}`.
Find
`(AxxB)nnn(AxxC)`
View SolutionLet `A={1,2,3}`,`B={3,4}` and `C={4,5,6}`.
Find
`Axx(BuuuC)`
View SolutionLet `A={1,2,3}`,`B={3,4}` and `C={4,5,6}`.
Find
`(AxxB)uuu(AxxC)`
View SolutionFind the domain and range of the following functions.
`f(x)=-abs[x]`
View SolutionFind the domain and range of the following functions.
`f(x)=sqrt(9-x^2)`
View SolutionFind the domain and range of the following functions.
`f(x)=abs[x-1]`
View SolutionFind the domain and range of the following
functions.
`f(x)=sqrt(x-1)`
View SolutionLet `A={1,2,3,4}` and `B={1,4,5}` be two sets.
If R is the relation "<" from A to B then
Write R in Roster form.
View SolutionLet `A={1,2,3,4}` and `B={1,4,5}` be two sets.
If R is the relation "<" from A to B then
Write Domain and Range of R.
View SolutionLet `A={1,2,3,4}` and `B={1,4,5}` be two sets.
If R is the relation "<" from A to B then
Find the number of relations from
A to B.
View SolutionIf `((2x)/5+1,y-3/4)=(1/5,1/4)` find x and y.
View SolutionIf `f={(2,5),(3,1),(5,2),(8,5),(10,2),(11,5)}`
is a function,write its range.
View SolutionLet `A={1,2,3}`,`B={3,4}`. Write a relation
from A and B having 5 elements. Write its
domain,co-domain and range.
View SolutionThe function f is defined by
`f(x)={(2-x,,x,<,0),(2,,x,=,0),(2+x,,x,>,0):}`
Draw the graph of Find `f(x)`
View SolutionLet `A={1,2,3}`,`B={4,5}`
Find `AxxB` and `BxxA`
View SolutionLet `A={1,2,3}`,`B={4,5}`
Find the number of relations from A to B.
View SolutionLet `A={7,8}` and `B={2,4,5}`. Find `AxxB`
View SolutionDetermine the domain and range of the
relation R defined by `R={(x,y):y=x+1}`,`x in {0,1,2,3,4,5,6}`
View SolutionIf `A={2,4}`,`B={1,3,5}`. Then the
number of relations from A to B
is …….
View SolutionIf `P={-1,1}`,form the set `PxxPxxP`.
View SolutionConsider the function `f:RrarrR` defined
by `f(x)=-abs[x]`
Find the domain and range of f.
View SolutionConsider the function `f:RrarrR` defined
by `f(x)=-abs[x]`
Draw the graph of f.
View SolutionConsider the functions
`f(x)=sqrt(x-2)`,`g(x)=(x+1)/(x^2-2x+1)`
Find
Domain of 'f'.
View SolutionConsider the functions
`f(x)=sqrt(x-2)`,`g(x)=(x+1)/(x^2-2x+1)`
Find
Domain of 'g'.
View SolutionConsider the functions
`f(x)=sqrt(x-2)`,`g(x)=(x+1)/(x^2-2x+1)`
Find
`(f+g)(x)`
View SolutionConsider the functions
`f(x)=sqrt(x-2)`,`g(x)=(x+1)/(x^2-2x+1)`
Find
`(fg)(x)`
View SolutionThe Cartesian product `PxxP` has 9 elements
among which are found `(-a,0)` and `(a,0)`.
A relation from P to P is defined as
`R={(x,y):x+y=0}`
Find P.
View SolutionThe Cartesian product `PxxP` has 9 elements
among which are found `(-a,0)` and `(a,0)`.
A relation from P to P is defined as
`R={(x,y):x+y=0}`
Depict the relation using an arrow
diagram.
View SolutionThe Cartesian product `PxxP` has 9 elements
among which are found `(-a,0)` and `(a,0)`.
A relation from P to P is defined as
`R={(x,y):x+y=0}`
Write down the domain and range of R.
View SolutionThe Cartesian product `PxxP` has 9 elements
among which are found `(-a,0)` and `(a,0)`.
A relation from P to P is defined as
`R={(x,y):x+y=0}`
How many relations are possible from P to P?
View SolutionConsider the real function `f(x)=(x+2)/(x-2)`
Find the domain and range of the function.
View SolutionConsider the real function `f(x)=(x+2)/(x-2)`
Prove that `f(x)f(-x)+f(0)=0`
View SolutionLet `P={1,2}`.Find `PxxPxxP`
View SolutionLet `A={1,2,3,……,13,14}`,R is the relation on A defined by `R={(x,y):3x-y=0 , x,y in A}`
Write R in a tabular form.
View SolutionLet `A={1,2,3,……,13,14}`,R is the relation on A defined by `R={(x,y):3x-y=0 , x,y in A}`
Find the domain and range of R.
View SolutionWrite the domain and range of the
relation
`R={(2,5),(3,10),(4,17),(5,26)}`
View SolutionIf `f(x)=x^2-3x` and `g(x)=x+2` find
`(f+g)(x)`,`(f-g)(x)` and `(fg)(x)`
View SolutionIf `P={m,n}`,`Q={n,m}` , state whether
the following is TRUE or FALSE
`PxxQ={(m,n),(n,m)}`
View SolutionWrite the relation `R={(x,x^3)`, x is a prime number less than 10}, in roster form.
View SolutionLet `A={1,2,3,4}` `B={1,5,9,11,15,16}` and `f={(1,5),(2,9),(3,1),(4,5),(2,1)}`. State with the reason whether f is a relation or a function.
View SolutionLet R be the set of Reals.Define a function
`f:RrarrR` by `f(x)=2x^2-1`
Find `(f(-1)+f(1))/2`
View SolutionLet R be the set of Reals.Define a function
`f:RrarrR` by `f(x)=2x^2-1`
Find `f[f(x)]`
View SolutionLet R be the set of Reals.Define a function
`f:RrarrR` by `f(x)=2x^2-1`
Draw the graph of `f(x)`
View SolutionIf `A={-1,1}`, find `AxxA`.
View SolutionConsider the relation R defined by `R={(x,x+1): x in {-1,1}}` Write R in the roster form. Also find the range.
View SolutionDraw the graph of the function.
`y=x`,`x in R`
View SolutionLet `A={1,2,3,4,5,6}` be a set. Defined a relation R from A to A by `R={(x,y)//y=x+1}`
Express R in the roster form.
View SolutionLet `A={1,2,3,4,5,6}` be a set. Defined a relation R from A to A by `R={(x,y)//y=x+1}`
Represent the relation R using an arrow diagram.
View SolutionLet `A={1,2,3,4,5,6}` be a set. Defined a relation R from A to A by `R={(x,y)//y=x+1}`
Write the domain and range of R.
View SolutionFind the domain of the function
`f(x)=(x^2+3x+5)/(x^2-5x+4)`
View SolutionSketch the graph of the function
`f(x)=abs[x+1]`
View SolutionMatch the following

View Solution`A={1,2,3,……,14}`. R is a relation from A to A defined by `R={(x,y): 3x-y = 0,x,y in A}`. Write the domain, range,co-domain of ,R.
View SolutionIf `(x+1,y-2)=(3,1)` , write the values of x and y.
View SolutionLet `A={1,2,3,4,5}` and `B={4,6,9}` be two sets. Define a relation R from A to B by
`R={(x,y):x-y}` is a positive integer.
View SolutionDefine the modulus function. What is
its domain? Draw a rough sketch.
View Solution
EXAMPLE questions and complete solutions for chapter Relations and Functions of MAXIMUM PUBLICATION of Class 11