Complete Solutions to EXAMPLE of chapter LIMITS AND DERIVATIVES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | LIMITS AND DERIVATIVES |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Evalute
`lim_(xrarr2)(x^2-5x+6)/(x^2-4)`
View SolutionEvalute
`lim_(xrarr2)(3x^2-x-10)/(x^2-4)`
View SolutionEvalute
`lim_(xrarr3)(x^4-81)/(2x^2-5x-3)`
View SolutionEvalute
`lim_(xrarr0)(sqrt(1+x)+sqrt(1-x))/(1+x)`
View SolutionEvalute
`lim_(xrarr1)(x^3-1)/(x-1)`
View SolutionEvalute
`lim_(xrarr0)(sin 5x)/(2x)`
View SolutionEvalute
`lim_(xrarr0)(e^(3x)-1)/(x)`
View SolutionFind the derivative of
`y=(x-a)(x-b)`
View SolutionFind the derivative of
`y=(ax^2+b)^2`
View SolutionFind the derivative of
`y=(x-a)/(x-b)`
View SolutionFind the derivative of
`y=x^(-3)(5+3x)`
View SolutionFind the derivative of
`y=(-2)/((x+1)^2)-x^2/(3x-1)`
View SolutionFind the derivative of
`y=(sin x)/x`
View SolutionFind the derivative of
`y=(ax+b)/(cx+d)`
View SolutionFind the derivative of
`y=(1+tan x)/(1-tan x)`
View SolutionIf `xy=c^2` , prove that `x^2dy/dx+c^2=0`
View SolutionEvalute : `lim_(xrarr0)((x+5)^2-25)/x`
View SolutionFind the derevative of `f(x)= x sin x`
View SolutionFind the derevative of `f(x)= (sin x)/x`
View SolutionEvalute `lim_(xrarr0)(sin ax)/(bx)`
View SolutionEvalute
`lim_(xrarr0)(sqrt(a^2+x^2)-sqrt(a^2-x^2))/x^2`
View SolutionEvalute
`lim_(xrarr2)(x^2-4)/(sqrt(3x-2)-sqrt(x+2))`
View SolutionEvalute
`lim_(xrarr0)(x^10-1024)/(x^5-32)`
View SolutionEvalute
`lim_(xrarr0)((x+1)^5-1)/(x)`
View SolutionEvalute
`lim_(xrarr0)((1-x)^n-1)/(x)`
View SolutionEvalute
`lim_(xrarr1)(z^(1/3)-1)/(z^(1/6)-1)`
View SolutionEvalute
`lim_(xrarr1)(1/x+1/2)/(x+2)`
View SolutionEvalute
`lim_(xrarr0)(sin ax)/(sin bx)`
View SolutionEvalute
`lim_(xrarr0)(sin^2 3x)/(x^2)`
View SolutionEvalute
`lim_(xrarr0)(1-cosx)/(x^2)`
View SolutionEvalute
`lim_(xrarrpi)(sin (pi-x))/(pi(pi-x))`
View SolutionEvalute
`lim_(xrarr0)(ax+ x cosx)/(b sin x)`
View SolutionEvalute
`lim_(xrarr0)(cos2x-1)/(cosx-1)`
View SolutionEvalute
`lim_(xrarrpi/2)(tan2x)/(x-pi/2)`
View SolutionEvalute
`lim_(xrarr0)(e^(ax)-1)/(e^(bx)-1`
View SolutionEvalute
`lim_(xrarr0)(log(1+x))/sinx`
View SolutionEvalute
`lim_(xrarr0)(e^x+e^-x-2)/x^2`
View SolutionEvalute
`lim_(xrarr0)(e^4-sin x-1)/x`
View SolutionEvalute
`lim_(xrarr0)(e^(sinx)-1)/(log(1+x))`
View SolutionFind `lim_(xrarr0) f(x)` and
`lim_(xrarr1) f(x)` where `f(x)={(2x+3,xle0), (3(x+1),x>0):}`
View SolutionFind `lim_(xrarr1) f(x)` where `f(x)={(x^2-1,xle1), (-x^2-1,x>1):}`
View SolutionEvalute
`lim_(xrarr0)f(x)` , where `f(x)={(absx/x, x ne 0),(0,x=0):}`
View SolutionFind the derevative of `y=tan x` from first principles.
View SolutionChoose the most appropriate answer from those given in bracket
If `lim_(xrarr2)(x^p-2^p)/(x-2)=192` then p=………
View Solution`lim_(xrarr0)(sqrt(1+x)-1)/x`
View SolutionChoose the most appropriate answer from those given in bracket
`lim_(xrarr0)(sin ax)/(x cos bx)` = ………
View Solution`lim_(zrarr1)(sqrtz-1)/(1-z)`=……….
View Solution`lim_(xrarrpi/4)(tan(pi/4-x))/((pi/4-x))`
View SolutionIf `lim_(xrarr0)(f(x))/(x^2)=k ne 0` then `lim_(xrarr1)f(x)`=……….
View SolutionUsing the first principal of derivatives , find the derivative of `1/x`.
View SolutionUsing the quotient rule find the derivative of `f(x)=cot x`
View SolutionFind the derivative of
`f(x)=(2x+3)/(x-1)`
View SolutionFind the derivative of
`f(x)=cos(x-5)`
View SolutionProve that `d/dx((cosx)/(1+sin x))=(-1)/(1+sinx)`
View SolutionFind the derivative of `y=cotx` from first principles.
View SolutionThe value of `lim_(xrarr0)(sinx)/x` is ……
View SolutionEvalute `lim_(xrarr0)(sin 4x)/(3x)`
View SolutionThe value of `lim_(xrarra)(x^n-a^n)/(x-a)` is ………
View SolutionEvalute `lim_(xrarr1)(x^(15)-1)/(x^(10)-1)`
View SolutionFind the derivative of `f(x)=sinx` from the first principle.
View SolutionFind the derivative of `(x+cosx)/(tanx)`
View SolutionFind the derivatives of `f(x)=sin x` using the first principle.
View SolutionFind the derivative of `(x^5-cosx)/(sinx)` using the quotient rule.
View SolutionUsing the first principle , find the derivative of `cos x`.
View SolutionFind the derivative of `(cosx)/(2x+3)`
View SolutionEvalute
`lim_(xrarr1)(x^7-1)/(x^4-1)`
View SolutionEvalute
`lim_(xrarr0)(cos2x-1)/(cosx-1)`
View SolutionEvalute `lim_(xrarrpi)(sin(pi-x))/(pi(pi -x))`
View SolutionCompute the derivative of `secx` with respect to `x` from first principle.
View SolutionFind `lim_(xrarr2)(x^4-4x^2)/(x^2-4)`
View SolutionIf `y=sin 2x` , Prove that `dy/dx=2cos2x`
View SolutionIf `f(x)={(a+bx,x<1),(4,x=1),(b-ax,x>1):}` and
`lim_(xrarr1)f(x)=f(1)` , then find the value of a and b.
View SolutionFind the derivative of `y=cosec x` from first principle.
View SolutionFind the derivative of `(x+1)/(x-1)` from first principle.
View SolutionThe value of `lim_(xrarr0)(sin 5x)/(5x)` is ………
View SolutionEvaluate `lim_(xrarr0)(sin ax)/(sin bx),a,b ne 0`
View SolutionFind the derivative of `1/x` from first principle.
View SolutionFind the derivative of
`(ax+b)^n(ax+c)^m`
View SolutionFind `lim_(xrarr-2)(x^2+5x+6)/(x^2+3x+2)`
View SolutionFind `f'(x)` given `f(x)=(x^2+5x+6)/(x^2+3x+2)`
View SolutionEvaluate `lim_(xrarr3)((x^3-27)/(x^2-9))`
View SolutionEvaluate `lim_(xrarr0)(tanx-sinx)/(sin^3x)`
View SolutionEvaluate `lim_(xrarr0)(sin5x)/(sin3x)`
View SolutionFind the derivative of `y=cos x` from the first principle.
View SolutionFind the derivative of `(sinx)/(x+cos x)`
View SolutionMatch the following :

View Solution`d/dx(tanx)`=…….
View SolutionFind the derivative of `3tanx+5secx`
View Solutionfind the derivative of `f(x)=(x^2+1)sinx`
View SolutionMatch the following :

View SolutionFind the derivative of `tan x` using first principle.
View SolutionMatch the following:
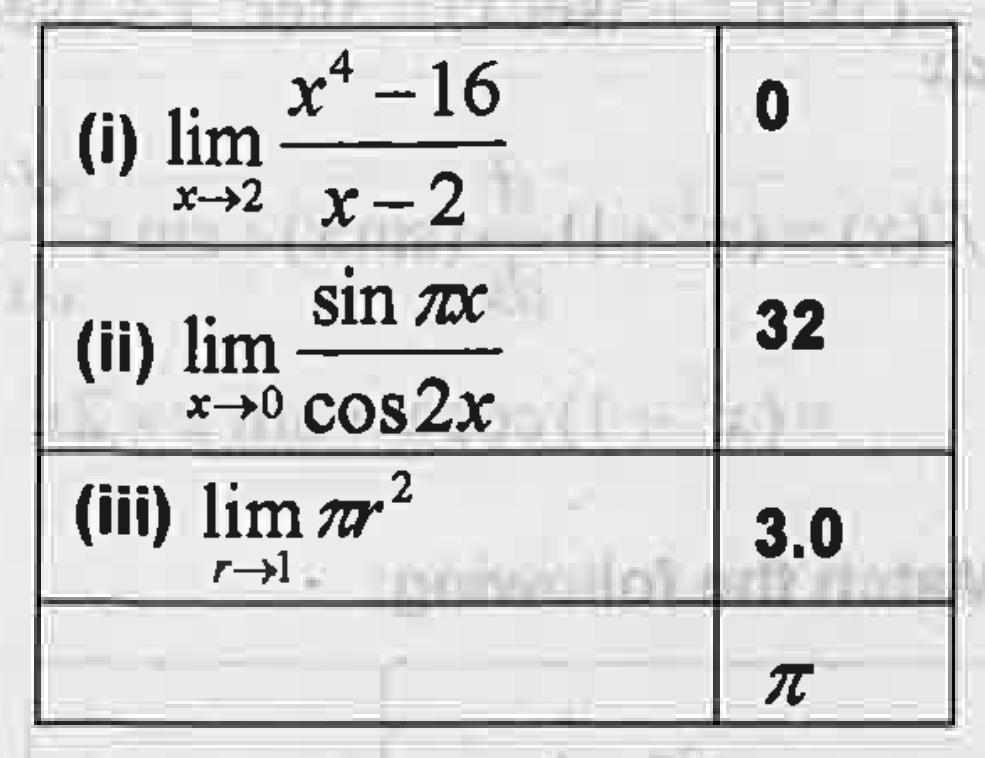
View SolutionIf `f(x)=x^(100)/100+x^(99)/99+......+x^2/2+x+1` prove that `f'(1)=100f'(0)`
View Solution`lim_(xrarr0)(tan x)/x`=………
View SolutionFind `lim_(xrarr0)(sin 4x)/(sin2x)`
View SolutionUsing the first principle , find the derivative of `cos x`.
View SolutionDerivative of `x^2-2` at `x=10` is ………..a)10 b)20 c)-10 d)-20
View Solution`f(x)={(2x+3,xle0),(3(x+1),x>0):}` find `lim_(xrarr0)f(x)` and `lim_(xrarr1)f(x)`.
View SolutionIf `xy=c^2` , prove that `x^2dy/dx+c^2=0`
View Solution`d/dx(x^n/n)`=……….
View Solution
EXAMPLE questions and complete solutions for chapter LIMITS AND DERIVATIVES of MAXIMUM PUBLICATION of Class 11