Complete Solutions to EXERCISE of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| MODERN PUBLICATION | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If A = { a, b,c}, B = {p,q}, find `BxxA` .
View SolutionLet A = {1, 2, 3, 4,5,6} and B = {2,4,6, 8}. Find `A xx B` .
View SolutionFind x and y if : (x+1,y -2) = (3,1)
View SolutionFind x and y if : (x+ 2,4) = (5, 2x+ y)
View SolutionIf `(x/3+1, y-2/3)=(5/3, 1/3)`, find the values of x and y.
View SolutionLet A= {1, 2, 3,4} and S = {(a, b) : a `in` A, b `in` A, a divides b}. Write S explicitly.
View SolutionLet A = {1, 2} and B = {3, 4}. Write `A xx B`. How many subsets will `A xx B` have? List them.
View SolutionLet A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2),(z, 1) are in `A xx B`, find A and B. where x, y and z are distinct elements.
View SolutionIf the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in `(A xx B)`.
View SolutionThe Cartesian product `A xx A` has 9 elements among which are found (-1, 0) and (0,1). Find the setA and the remaining elements of `A xx A`.
View SolutionIf A= {-1, 1}, find `A xx A xx A`.
View SolutionIf R is the set of all real numbers. what do the cartesian products `R xx R` and `R xx R xx R` represent ?
View SolutionIf `A xx B` = {(a, x).(a , y). (b, x), (b, y)}. Find A and B.
View SolutionIf A = { 1, 2}, B = {3, 4}, C = {4, 5}, find `A xx (B uu C)`.
View SolutionIf A={a, b,c}, B= {c, d} and C= {d, e, f}, find : `(A nn B)xxC`.
View SolutionIf A={a, b,c}, B= {c, d} and C= {d, e, f}, find : `(A xx B) nn (BxxC)`.
View SolutionLet A = {1, 2, 4}, B= {3, 5, 7} and C = {5, 7, 9}, find `A xx (B nn C)`.
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C = {4, 5, 6}. Find : `(A xx B) nn (AxxC)`.
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C = {4, 5, 6}. Find : `(A xx B) nn (AxxC)`.
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C = {4, 5, 6}. Find : `Axx (B uu C)`.
View SolutionLet A= {1, 2, 3}, B= {3, 4} and C = {4, 5, 6}. Find : `(A xx B) nn (AxxC)`.
View SolutionLet A = {2, 4, 6}, B= {6, 8, 10} and C = {10, 12,14}. Find `B xx (A uu C)`.
View SolutionLet `A = {1/2,2}`, B = {2,3,5}, C= {-1,- 2}. Verify that : `A xx (B nn C)= (AxxB)nn (AxxC)`.
View SolutionLet A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2),(z, 1) are in `A xx B`, find A and B. where x, y and z are distinct elements.
View SolutionThe Cartesian product `A xx A` has 9 elements among which are found (-1, 0) and (0,1). Find the setA and the remaining elements of `A xx A`.
View SolutionLet A = {1, 2, 3}, B= {2, 3, 4} and C= {4, 5}. Verity that : `A xx (Buu C)= (A xxB) uu (A xx C)`.
View SolutionIf A= {1, 2, 3}, B= {4},C = {5}. then verify that : `A xx (Buu C)= (A xxB) uu (A xx C)`.
View SolutionIf A= {1, 2, 3}, B= {4},C = {5}. then verify that : `A xx (B nn C)= (A xxB) nn (A xx C)`.
View SolutionIf A= {1, 2, 3}, B= {4},C = {5}. then verify that : `A xx (B - C)= (A xxB) - (A xx C)`.
View SolutionLet A= {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} andD = {5, 6, 7, 8}. Verify that `A xx C` is a subset of `B xx D`.
View SolutionLet A= {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} andD = {5, 6, 7, 8}. Verify that `A xx (B nn C) = (A xx B) nn (A xx C)`.
View SolutionLet A = {1, 2, 3}, B= {- 1,0, 1,2,3} and C= {1}, D={- 1,1}. Then Verify the following : `(A xxB) nn (C xx D) =(A nn C) xx (B nn D)`.
View SolutionLet A = {1, 2, 3}, B= {- 1,0, 1,2,3} and C= {1}, D={- 1,1}. Then Verify the following : If `A sub B` and `C sub D`, then `(A xxC) sub (BxxD)`.
View SolutionLet P = {1, 4,9} and Q= {2,4,6}. Write the elements of `(P nn Q)xx (P uu Q)`. Also find `(P xx Q) nn (Q xx P)`.
View SolutionIfA and B are non-empty sets and A `xx` B=B `xx` A, then
View SolutionLet A be a non-empty set such that `AxxB=AxxC`. Show that B = C.
View SolutionProve that `A sube B` and `C sube D` imply : `(A xxC) sube (B xxD)`.
View SolutionIf `A sube B`, prove that `AxxA sube (A xxB) nn (BxxA)`.
View SolutionIf `A sube B`, prove that `AxxC sube BxxC` for any set C.
View SolutionFor any three sets A, B,C prove that : `Axx (B uu C)= (AxxB) uu (AxxC)`.
View SolutionFor any three sets A, B,C prove that : `(A- B) xx C= (AxxC) - (BxxC)`.
View SolutionFor any three sets A, B,C prove that : `Axx (B uu C)= (AxxB) uu (AxxC)`.
View SolutionFor any three sets A, B,C prove that : `(A nn B) xx C= (AxxC) nn (BxxC)`.
View SolutionFor any four sets A, B, C and D, prove that : `(A nn B)xx (C nn D)= (AxxC) nn (BxxD)`.
View SolutionFor any three sets A, B,C prove that : `Axx(B^(c) uu C^(c))^(c)= (AxxB) nn (AxxC)`.
View SolutionFor any three sets A, B,C prove that : `Axx(B^(c) nn C^(c))^(c)= (AxxB) uu (AxxC)`.
View SolutionState whether the following statement is true or false. If the statement is false, rewrite the given statement correctly. ) If P = {m, n} and Q = { n, m}, then `P xx Q` = {(m, n),{n. m)}.
View SolutionState whether the following statement is true or false. If the statement is false, rewrite the given statement correctly. If A and B are non-empty sets, then `A xx B` is a non-empty set of ordered pairs (x, y) such that `x in A` and `y in B`.
View SolutionState whether the following statement is true or false. If the statement is false, rewrite the given statement correctly. If A = {1, 2}, B = {3, 4}, then `A xx (B nn phi) = phi`.
View SolutionIf A= {1, 2, 3} and B = {1, 2}, then find : `AxxB`.
View SolutionIf A= {1, 2, 3} and B = {1, 2}, then find : `B xx A`.
View SolutionIf A= {1, 2, 3} and B = {1, 2}, then find : Is `AxxB= B xx A` ?
View SolutionIf A= {1, 2, 3} and B = {1, 2}, then find : Represent `AxxB` graphically and by arrow diagram.
View SolutionLet X = {- 2,0, 1}, Y = {2, 3}. Represent `X xx Y` and `Y xx X` graphically.Also find `n (X xx Y )` and `n(Y xx X)`.
View SolutionLet A = {2, 3, 5, 7}, B = (1, 12, 13, 15}. How many elements are there in `AxxB`? In `Bxx A`? Is `AxxB = BxxA?` Is `n(AxxB)=n(BxxA)`?
View SolutionIf A and B are two non-empty sets having n elements in common, then prove that `Axx B` and `B xx A` have `n^2` elements in common.
View SolutionLet A = {x, y,z} and B = {1,2}. Find the number of relations from A to B.
View SolutionLet A = {1, 2}. List all relations on A.
View SolutionA = {1, 2, 3, 5} andB= {4, 6, 9}. Define a relation R Ifom A to B by R = {(x,y): the difference between x and y is odd, `x in A, y in B`}. Write R in roster form.
View SolutionWrite the relation R = {(x, `x^3`) : x is a prime number less than 10} in roster form.
View SolutionLet R be the relation on Z defined by R = {(a,b ): a, b `in` Z, a-b is an integer}. Find the domain and range of R.
View SolutionLet A = {3,5} and B = {7, 11}. Let `R = {(a, b):a in A, b in B, a -b` is odd}. Show that R is an empty relation from A into B.
View SolutionWhich of the following graphs of relations defines a transitive relation in A = {1, 2, 3, 4} ? `R_1 = {(1, 2), (3, 4), (2, 3), (2, 4)}`, `R_2 = (1, 2), (3, 4), (2, 4)}`.
View SolutionLet R be the relation on Z defined by aRb if and only if a -b is an even integer. Find : R.
View SolutionLet R be the relation on Z defined by aRb if and only if a -b is an even integer. Find : domain of R.
View SolutionLet R be the relation on Z defined by aRb if and only if a -b is an even integer. Find : range of R.
View SolutionLet R be the relation on Z defined by : `R ={(a,b) :a in Z,b in Z, a^2 =b^2}`. Find : R.
View SolutionLet R be the relation on Z defined by : `R ={(a,b) :a in Z,b in Z, a^2 =b^2}`. Find : domain of R.
View SolutionLet R be the relation on Z defined by : `R ={(a,b) :a in Z,b in Z, a^2 =b^2}`. Find : range of R.
View SolutionLet A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8, 10}. Let `R = {(a, b): a in A, b in B`, a divides b} be a relation from A into B. Find R. Show that domain of R is A and range of R is B.
View SolutionDetermine the domain and range of the relation R defined by : `R = {(x+1,x+5):x in {0, 1, 2, 3, 4, 5}}`.
View SolutionDetermine the domain and range of the relation R defined by : `R = {(x, x^3): x` is prime number less than 10}.
View SolutionDetermine the domain and range of the following relation : {(1,2), (1,4), (1,6), (1,8)}.
View SolutionDetermine the domain and range of the following relation : `{(x,y): x in N , y in N and x + y= 10}`.
View SolutionDetermine the domain and range of the following relation : `{(x,y): x in N , x<5, y=3}`.
View SolutionDetermine the domain and range of the following relation : `{(x,y): y =|x-1|,x in Z` and `|x| le3 }`.
View SolutionLet A = {1, 2, 3, 4} and B = {x,y,z}. Let R be a relation from A into B defined by : R= {(1,x), (1,z), (3,x), (4,y)}. Find the domain and range of R.
View SolutionShow that the relation ‘is perpendicular to' on the set A of all coplanar straight lines is symmetric but it is neither reflexive nor transitive.
View SolutionShow that `R= {(a, b): a ge b}` is reflexive and transitive but not symmetric.
View SolutionShow that the relation ‘is a factor of’ on the set N of all natural numbers is reflexive and transitive but not symmetric.
View SolutionLet A = {1, 2, 3, .........., 14}. Define a relation R from A to A by R = {(x,y): 3x-y=0, where x, y `in` A}. Depict this relationship using an arrow diagram.
View SolutionDefine a relation R on the set N of natural numbers by : R= {(x, y): y =x + 5, x is a natural number less than 4, x, y `in` N}. Depict this relationship using (i) roster form (ii) an arrow diagram.
View SolutionLetA= {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a ,`b in A`, b is exactly divisible by a}. Write R in roster form
View SolutionLetA= {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a ,`b in A`, b is exactly divisible by a}. Find the domain of R
View SolutionLetA= {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a ,`b in A`, b is exactly divisible by a}. Find the range of R.
View SolutionThe following figure shows a relation between P and Q. Write the relation in : set builder form. What is its domain and range ?
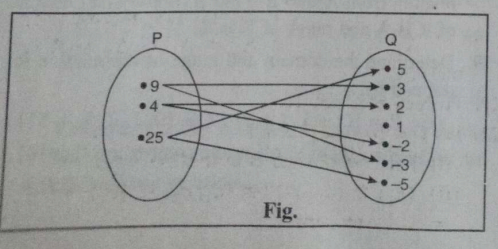
View SolutionThe following figure shows a relation between P and Q. Write the relation in : roster form. What is its domain and range ?
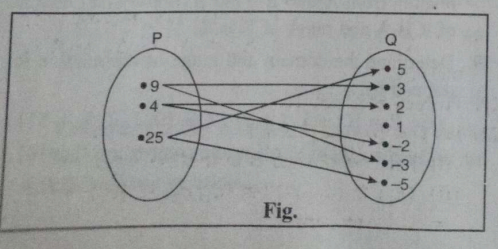
View SolutionFor the given relation R on a set S, determine which are equivalence relations : (i) S is the set of all rational numbers a R b iff a= b. (ii) S is the set of all real numbers iff : (I) `|a |= |b|` (II) `a ge b`.
View SolutionFor the given relation R on a set S, determine which are equivalence relations : (i) S is the set of all rational numbers a R b iff a= b. (ii) S is the set of all real numbers iff : (I) `|a |= |b|` (II) `a ge b`.
View SolutionIf R is the relation in `N xx N` defined by (a, b) R (c,d) if and only if (a + d) =(b + c), show that R is an equivalence relation.
View SolutionIs inclusion of a subset in another, in the context of a universal set, an equivalence relation in the class of subsets of the sets ? Justify your answer.
View SolutionGiven the relation R = {(1, 2), (2, 3)} on the set of natural numbers, add a minimum of ordered pairs so that the enlarged relation is symmetric, transitive and reflexive.
View SolutionLet `f(x) = x^2` and g(x) = 2x + 1 be two real functions. Find : (f + g) (x), (f-g)(x), (fg) (x) and `(f/g)` (x).
View SolutionLet `f(x)= sqrtx` and g (x) = x be two functions defined over the set of non-negative real numbers. Find (f+ g) (x), (f-g)(x), (fg) (x) and `(f/g)` (x).
View SolutionIf f and g are functions defined by : `f(x)= sqrt(x-1), g(x)=1/x`,then describe the following : f+g.
View SolutionIf f and g are functions defined by : `f(x)= sqrt(x-1), g(x)=1/x`,then describe the following : f-g.
View SolutionIf f and g are functions defined by : `f(x)= sqrt(x-1), g(x)=1/x`,then describe the following : fg.
View SolutionIf f and g are functions defined by : `f(x)= sqrt(x-1), g(x)=1/x`,then describe the following : `f/g`.
View SolutionDefine the real valued function f:R- {0} `rarr` R defined by `f(x) = 1/x,x in R-{0}`. Complete the table given below using this definition. What is the domain and range of this function.

View SolutionSketch the graph of the following function : ` f(x)= 4- 2x`. Also find its domain and range.
View Solution
EXERCISE questions and complete solutions for chapter RELATIONS AND FUNCTIONS of MODERN PUBLICATION of Class 11