Complete Solutions to EXAMPLE of chapter LINEAR INEQUATIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | LINEAR INEQUATIONS |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
Solve the following inequation :
`3x-7> 5x-1`.
View SolutionSolve the following inequation :
`3(2-x)ge2(1-x)`.
View SolutionSolve the following inequation for real x:
`(5-2x)/3 lex/6-5`.
View SolutionSolve the following inequalities:`6le-3(2x-4)<12`.
View SolutionSolve the following inequation :
`7le (3x+11)/2 le11`.
View SolutionSolve `7x+3< 5x+9`. Show the graph of the solution on the number line.
View SolutionSolve the following inequation :
`3x-6 <0`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`-3x+9le0`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`7x+5 >33`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`5x-15 ge0`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`4x +3 < 6x +7`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`5x -1>3x +7`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`(3(x-2))/5 ge (5(2-x))/3`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`x/4< (5x-2)/3-(7x-3)/5`. Show the graph of the solution on the number line .
View SolutionSolve the following inequation :
`(x-3)/(x-5) >0`.
View SolutionSolve the following inequation :
`(x+3)/(x-2) le2`.
View SolutionSolve : `(2x-3)/4+8ge2+(4x)/3` and show the solution set on the number line.
View SolutionSolve 20x < 100, when : x is a natural number.
View SolutionSolve `24x < 100`, when x is an integer.
View SolutionSolve `5x -3 < 7`, when x is an integer.
View SolutionSolve `5x -3 < 7`, when x is a real number.
View SolutionSolve
3x + 5 < x-7, when: x is an integer. Show the graph of the solution set on the number line .
View SolutionSolve
3x + 5 < x-7, when: x is an integer. Show the graph of the solution set on the number line .
View SolutionSolve the system of inequations : `x-2 >0, 3x < 18`.
View SolutionSolve the following system of inequalities : `3x - 7 lt 5 + x` and `11 - 5x le 1` and represent the solution on number line.
View SolutionSolve the following system of inequalities : `3x - 7 lt 5 + x` and `11 - 5x le 1` and represent the solution on number line.
View SolutionSolve the following system of inequations : `(5x)/4+(3x)/8 > 39/8` and `(2x-1)/12-(x-1)/3 < (3x+1)/4`.
View SolutionSolve the following system of inequations : `2(2x + 3)-10<6(x -2)` and `(2x-3)/4+ 6 ge2+ (4x)/3`.
View SolutionRepresent the following inequations graphically in two-dimensional plane and hence solve them :
` x>-2`.
View SolutionRepresent the following inequations graphically in two-dimensional plane and hence solve them :
`y<3`.
View SolutionRepresent the following inequations graphically in two-dimensional plane and hence solve them :
`2x -3 ge 0`.
View SolutionRepresent the following inequations graphically in two-dimensional plane and hence solve them :
`yle -3`.
View SolutionSolve graphically : `|x| <2`.
View SolutionSolve graphically : `|y| ge 3`.
View SolutionSolve graphically the inequation `x+2y- 4<0`.
View SolutionDraw the graph of the inequation `3x- 5y +8 ge 0`.
View SolutionDraw the diagram of the solution set of the linear constraints :
`3x+4y ge 12,y ge 1,x ge 0`.
View SolutionDraw the diagram of the solution set of the linear constraints :
`2x+3y le 6,x+ 4y le 4,x ge 0,y ge 0`.
View SolutionFind the linear constraints for which the shaded area in the figure below is the solution set.
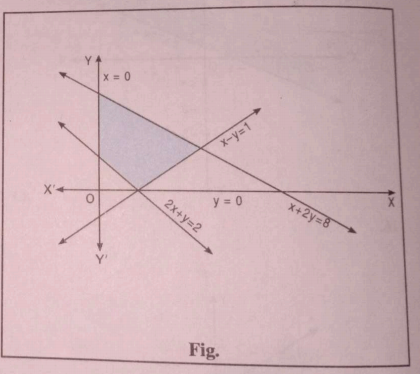
View SolutionVerify that the solution set of the following is empty : `x-2yge0,2x-yle-2,xge0,yge0`
View SolutionFind graphically the solution set of the following :
`2x+y ge 4` and `x-y+1=0`.
View SolutionFind graphically the solution set of the following :
`2x+y+3 le 0` and `2x+y-4 ge 0`.
View SolutionFind the region enclosed by the following inequations : `x+y-2 le 0,2x+y-3 le 0,x ge 0,y ge 0`. Also find the ordered pairs of the vertices of the regions.
View SolutionRavi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
View SolutionFind all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
View SolutionIn the first four examinations, each of 100 marks, Hamid got 94,73,72, 84 marks if the final average is greater than or equal to 80 and less than 90 is needed to obtain a final B grade in a course, what range of marks in the fifth (last) examination will result in Hamid receiving 'B' in the course ?
View SolutionIn an experiment, a solution of a hydrochloric acid is to be kept between `30^@` and `35^@`C. what is the range of the temperature in degree fahrenheit, if conversion formula is given by
`C=5/9 (F-32)`
Where C and F represent temperature in degree celsius and degree fahrenheit respectively.
View SolutionIQ of a person is given by the formula `IQ= (MA)/(CA)xx100` , where MA is mental age and CA is chronological age. If `80 le IQ le 140` for a group of 12 years old children, find the range of their mental age.
View SolutionA manufacture has 600 litres of a `12%` solution of acid .How many litres of a `30%` acid solution must be added to it so that acid content in the resulting mixture will be more than `15%` but less than `18%` ?
View SolutionBy the Principle of Mathematical Induction, prove the following for all n `in` N :
`4^(n)-3n-1` is divisible by 9.
View SolutionProve that : `7^(2n)+(2^(3n-3))(3^(n-1))` is divisible by 25 `forall n in N`.
View SolutionGiven `n^4 <10^n` for a fixed integer `nge 2`. Prove that `(n+1)^4 <10^(n+1)`.
View SolutionLet `U_1 =1, U_2=1` and `U_(n+2)=U_(n+1)+U_n` for `nge1`. Use Mathematical Induction to show that: `U_n= 1/sqrt5[((1+sqrt5)/2)^n-((1-sqrt5)/2)^n]` for all `n ge1`.
View SolutionApply the principle of Mathematical Induction to prove that : `|sin nx| le n|sin x|` for all n `in` N.
View SolutionLet a, b, c be positive real numbers such that `b^2- 4ac > 0` and let `alpha_1 = c`. Prove by induction that `alpha_(n+1)= (a alpha_n^2)/(b^2 -2a(alpha_1+alpha_2+...+alpha_n))` is well defined and `alpha_(n+1) ltalpha_n/2` for all `n = 1, 2, ..... `(Here, ‘well defined’ means that the denominator in the expression for `alpha_(n+1)`is not zero).
View SolutionSolve the equation |z|+z=2+i, where z = x + iy.
View SolutionIf z is a complex number which simultaneously satisfies the equations
`3abs(z-12)=5abs(z-8i) " and " abs(z-4) =abs(z-8)`, where `i=sqrt(-1)`, then Im(z) can be
View SolutionFind all the roots of the equation : `(3z -1)^4+(z-2)^4 =0` in the simplified form of a + ib.
View SolutionUse De-Moivre’s Theorem to solve the equation: `2 sqrt2 x^4= (sqrt3-1)+i(sqrt3+1)`.
View SolutionGiven that : `(a_1 + ib_1) (a_2 + ib_2) ... (a_n + ib_n) = c + id`, show that : `tan^-1 (b_1/a_1)+tan^-1 (b_2/a_2)+.............+ tan^-1 (b_n/a_n)= n pi+ tan^-1 (d/c)`.
View SolutionShow that the area of the triagle on the argand plane formed by the complex numbers Z, iz and `z+iz`is `(1)/(2)|z|^(2)," where "i=sqrt(-1).`
View Solutionlet `z_(1=10+6i,z_(2)=4+6i,where
i=sqrt((-1)).` If z is a complex number , such that the argument of `(z-z_(1))//(z-z_(2))ispi//4,` then prove that`|z-7-9i|=3sqrt(2).`
View SolutionLet `bar b z+b bar z=c, b ne 0`, be a line in the complex plane, where`bar b` is the complex conjugate of b. If a point `z_1` is the reflection of a point `z_2` through the line, then show that : `c= bar z_1 b+z_2 bar b`.
View SolutionFor complex numbers z and w, prove that `|z|^2 w -|w|^2 z = z - w `if and only if z=w or `z bar w= 1`.
View SolutionLet the complex numbers `z_1,z_2,z_3` be the vertices of an equilateral triangle. Let `z_0` be the circumcentre of the triangle. Then prove that `z_1^2+z_2^2+z_3^2= 3z_0^2`.
View Solution
EXAMPLE questions and complete solutions for chapter LINEAR INEQUATIONS of MODERN PUBLICATION of Class 11