Complete Solutions to EXAMPLE of chapter PERMUTATIONS AND COMBINATIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | PERMUTATIONS AND COMBINATIONS |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 98 |
| Academic Year | 2023-24 |
Evaluate 8!.
View SolutionFind `(7!)/(5!)`.
View SolutionCompute `(52!)/((47!)(5!))`.
View SolutionCompute `(4!)(2!)`. Is `(4!)(2!)=8!`?
View SolutionWhen n = 5 and r = 2, find the values of : `(n!)/(r!)`.
View SolutionWhen n = 5 and r = 2, find the values of : `(n!)/(r!(n-r)!)`.
View SolutionIf `1/(6!)+1/(7!)=x/(8!)`, find x
View SolutionProve that : `(2n) ! = 2^n (n!)[1.3.5.... (2n-1)]` for all natural numbers n.
View SolutionProve that `(n!)^2 le n^n. (n!)<(2n)!` for all positive integers n.
View SolutionProve that n!+1 is not divisible by any integer between 2 and n.
View SolutionProve that 33! Is divisible by `2^(19)` and what is the largest integer n such that 33! Is divisible by `2^(n)`?
View SolutionA lady wants to select one cotton saree and one polyester saree from a textile shop. If there are 10 cotton varieties and 12 polyester Varieties, in how many ways can she choose the two sarees ?
View SolutionHow many three-digit numbers can be formed without using the digits 0, 2, 3, 4, 5 and 6?
View SolutionHow many 2-digit even numbers can be formed from the digits 1, 2,3, 4 and 5, if the digits can be repeated ?
View SolutionHow many numbers are there between 100 and 1000 such that every digit Is either 2 or 9?
View SolutionIn a class there are 30 boys and 18 girls. The teacher wants to select one boy and one girl to represent the class for a quiz competition. In how many ways can the teacher make this selection ?
View SolutionHow many 3-letter code words are possible using the first 10 letters of English alphabet if : no letter can be repeated ?
View SolutionHow many 3-letter code words are possible using the first 10 letters of English alphabet if : letters are repeated ?
View SolutionIt has been decided that the flag of a newly formed forum will be in the form of three blocks, each coloured differently. If there are six colours on the whole to choose from, how many designs are possible ?

View SolutionIn how many ways can the following diagram be coloured subject to the following conditions ?
 Each of the smaller triangle is to be painted with one of the three colours, red, blue or green.
Each of the smaller triangle is to be painted with one of the three colours, red, blue or green.
View SolutionIn how many ways can the following diagram be coloured subject to the following conditions ?
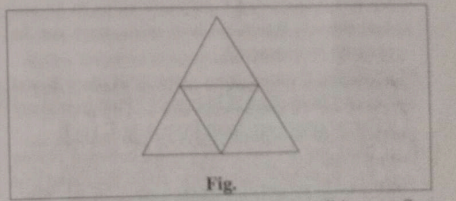 No two adjacent regions receive the same colour .
No two adjacent regions receive the same colour .
View SolutionIn how many ways can 5 persons sit in a car, 2 including the driver in the front seat and 3 in the back seat, if 2 particular persons out of the 5 are to avoid the driver's seat ?
View SolutionThere are 4 multiple-choice questions in an examination. How many sequence of answers are possible, if each question has 2 choices ?
View SolutionFind the number of different signals that can be generated by arranging at least 2 flags in order (one below the other) on a vertical staff, if five flags are available.
View SolutionFind the value of `"^4P_3`.
View SolutionFind n if `"^nP_4 = 20 ^nP_2`.
View SolutionFind the value of n such that :
`"^nP_5=42 ^nP_3, n>4`.
View SolutionFind the value of n such that :
`('^nP_4)/("^(n-1)P_4)= 5/3, n>4`.
View SolutionProve that if `r le s le n`, then `""^nP_s` is divisible by `""^nP_r` .
View SolutionProve that : `^nP_r= "^(n-1)P_r+r ^(n-1)P_(r-1)`, for all natural numbers n and r for which the symbols are defined.
View SolutionProve that : ` ^nP_r= n"^(n-1)P_(r-1)`, for all natural numbers n and r for which the symbols are defined.
View SolutionProve that
`.^(1)P_(1)+2*.^(2)P_(2)+3*.^(3)P_(3)+ . . .+n*.^(n)P_(n)=.^(n+1)P_(n+1)-1`.
View SolutionHow many three-digit numbers are there, with distinct digits, with each digit odd ?
View SolutionHow many different 6-digit numbers can be formed with the digits 0, 1, 3, 5, 7 and 9 ? (No digit being repeated.)
View SolutionHow many of them are divisible by 10 if 6 digit numbers formed by 0,1,3,5,7,9 when no digit repeated?
View SolutionHow many numbers greater than 56000 can be formed by using the digits 4, 5, 6,7, 8, no digit being repeated in any number ?
View SolutionSix candidates are called for interview to fill four posts in an office. Assuming that each candidate is fit for each post. determine the number of ways in which : first and second posts can be filled.
View SolutionSix candidates are called for interview to fill four posts in an office. Assuming that each candidate is fit for each post. determine the number of ways in which : first three posts can be filled.
View SolutionSix candidates are called for interview to fill four posts in an office. Assuming that each candidate is fit for each post. determine the number of ways in which : all the four posts can be filled.
View SolutionHow many signals can be made by hoisting 5 flags of different colours ?
View SolutionFind the number of permutations of n things taken r at a time in which two particular things : always occur.
View SolutionFind the number of permutations of n things taken r at a time in which two particular things : never occur.
View SolutionIn how many ways can six different rings be worn on the four fingers of one hand ?
View SolutionHow many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming (i) repetition of digits allowed (ii) repetition of digits not allowed ?
View SolutionThere are three prizes to be distributed among 6 students. In how many ways can this be done when
no boy gets more than one prize.
View SolutionThere are three prizes to be distributed among 6 students. In how many ways can this be done when
there is no resrtiction as to the number of prizes that a boy may get.
View SolutionThere are three prizes to be distributed among 6 students. In how many ways can this be done when
no boy gets all prizes.
View SolutionHow many 7-digit numbers can be formed, using the digits 1, 2, 0, 2, 4,2 and 4?
View SolutionHow many numbers can be formed with the digits 1, 2, 3, 4, 3, 2, 1 so that odd digits always occupy the odd places?
View SolutionIn how many ways can 4 red, 3 yellow and 2 green discs be arranged if the discs of the same colour are indistinguishable ?
View SolutionHow many permutations of the letters of the word “APPLE” are there ?
View SolutionHow many different words can be formed with the letters of the 'BHARAT' ? In how many of these B and H are never together ?
View SolutionHow many different words can be formed with the letters of the 'BHARAT' ? How many of these begin with B and end with T ?
View SolutionIf the different permutations of all the letter of the words 'EXAMINATION' are listed as in a dictionary, how many words are there in this list before the first word starting with E?
View SolutionA code word is to consist of two English alphabets followed by two distinct numbers between 1 and 9. For example, CA23 is a code word. How many such code words are there? How many of them end with an even integer ?
View SolutionFind the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do the words start with P ?
View SolutionFind the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do all the vowels always occur together ?
View SolutionFind the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do the vowels never occur together ?
View SolutionFind the number of arrangements of the letters of the word ‘INDEPENDENCE’. In how many of these arrangements, do the words begin with I and end in P ?
View SolutionNumber of ways in which is 8 boys can sit in a circle?
View SolutionIn how many ways can 8 students be seated in : a line ?
View SolutionThere are 6 gentlemen and 3 ladies to dine at a round table. In how many ways can they seat themselves so that no two ladies are seated together ?
View SolutionIn how many ways can 6 beads of same colour form a necklace ?
View SolutionThree boys and three girls are to be seated around a table in a circle. Among them, the boy X does not want any girl neighbour and the girl Y does not want any boy neighbour. How many such arrangements are possible ?
View SolutionEvaluate `"^10C_4`.
View SolutionVerify that `2 C (7,4)= C(8,4)`.
View SolutionIf `" C(n,7)= C(n,5)`, find `C(n,4)`.
View SolutionProve that : `^2C_1+ ^3C_1+ ^4C_1= "^3C_2+ ^4C_2`.
View SolutionProve that `underset (r=1) overset (5) sum "^5C_r=31`.
View SolutionProve that : `^(2n)C_n = (2^n [1.3.5. ..........(2n-1)])/(n!)`.
View SolutionFind n, if `""^(2n)C_(1),""^(2n)C_(2)` and `""^(2n)C_(3)` are in A.P.
View SolutionProve that the product of 2n consecutive negative integers is divisible by (2n)! .
View SolutionHow many different teams of 7 payers can be chosen from 10 players ?
View SolutionHow many chords can be drawn through 21 points on a circle?
View SolutionNumber of diagonals in a hexagon are
(i) 6
(ii) 5
(iii) `underline(9)`
View SolutionFrom a class of 32 students, 4 are to be chosen for a competition. In how many ways can this be done ?
View SolutionA bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
View SolutionA committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: exactly 3 girls ?
View SolutionA committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of : at least three girls.
View SolutionA committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of: atmost 3 girls ?
View SolutionWhat is the number of ways of choosing 4 cards from a pack of 52 playing cards, if
four cards are of the same suit,
View SolutionWhat is the number of ways of choosing 4 cards from a pack of 52 playing cards, if
four cards belong to four different suits,
View SolutionWhat is the number of ways of choosing 4 cards from a pack of 52 playing cards, if
they are face cards.
View SolutionWhat is the number of ways of choosing 4 cards from a pack of 52 playing cards ? In how many of these : two are red cards and two are black cards?
View SolutionWhat is the number of ways of choosing 4 cards from a pack of 52 playing cards ? In how many of these : cards are of the same colour ?
View SolutionIn an examination, a question paper consists of 12 questions divided into parts i.e. Part I and Part II, containing 5 and 7 questions respectively. A student is required to attempt 8 questions, selecting at least 3 from each part.In how many ways can a Student select the questions ?
View SolutionA Student has to answer 10 questions, choosing at least 4 from each of part A and part B. If there are 6 questions in part A and 7 questions in part B, in how many ways can the student choose 10 questions?
View SolutionA person wishes to make up as many different parties as he can out of his 16 friends such that each party consists of the same number of persons. How many friends should be invite ?
View SolutionA sports team of 11 students is to be constituted, choosing at least 5 from class XI and at least 5 from class XII. If there are 20 students in each of these classes, in how many ways can the teams be constituted ?
View SolutionIn a village, there are 87 families, of which 52 families have atmost 2 children. In a rural development programme, 20 families are to be chosen for assistance, of which at least 18 families must have atmost 2 children. In how many ways can the choice be made ?
View SolutionIf m parallel lines in a plane are intersected by a family of n parallel lines, find the number of parallelograms formed.
View SolutionIn how many ways can 10 things be equally divided : between two persons?
View SolutionIn how many ways can 10 things be equally divided : into two heaps ?
View SolutionA man has 6 friends. In how many ways can he invite one or more of his friends to a party ?
View SolutionFrom 4 mangoes, 5 oranges and 6 apples, how many selections of fruits can be made by taking at least one of them ?
View SolutionA number lock on a suitcase has 3 wheels each labeled with ten digits from 0 to 9. If the opening of the lock is a particular sequence of three digits with no repeats, how many such sequences will be possible?
View SolutionA customer forgets a four-digit code of an Automatic Teller Machine (ATM) in a bank. However, he remembers that this code consists of digits 2, 3, 6 and 9. Find the largest possible number of trails necessary to obtain the correct code.
View SolutionGive expressins in the following cases:
7 added to p.
View Solution
EXAMPLE questions and complete solutions for chapter PERMUTATIONS AND COMBINATIONS of MODERN PUBLICATION of Class 11